Hans Walser
Universitt Basel
Schwerpunkt
Forum fr Begabtenfrderung
22. bis 24. Mrz 2012, TU
Berlin
Zusammenfassung
Beim Schwerpunkt
treffen Geometrie und Physik aufeinander. Dies erffnet interessante Einsichten
und Querverbindungen. Es kommen Beispiele am Dreieck und Viereck zur Sprache.
Insbesondere wird auf die Unterschiede von Eckenschwerpunkt, Kantenschwerpunkt
und Flchenschwerpunkt eingegangen. Schlie§lich wird eine bemerkenswerte Gerade
im Viereck vorgestellt.
Fachliche und
didaktische Zielsetzung: Querbezge zwischen Bereichen der Elementargeometrie,
der Mechanik und der Topologie. Frderung des Raumvorstellungsvermgens.
1
Eine falsche Argumentation
An einer
Fachdidaktiker-Tagung wurde so nebenbei der Satz formuliert, eine Gerade durch
den Schwerpunkt halbiere die Flche. Das Argument dafr war, dass der Schwerpunkt
ja gerade so definiert worden sei (Abb. 1).
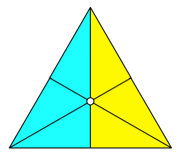
Abb. 1: Halbierung der
Flche
Sehen wir uns die Sache
nher an. Wir parkettieren das Dreieck und legen eine horizontale Linie durch
den Schwerpunkt (Abb. 2).
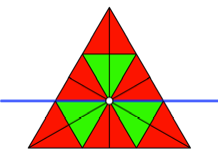
Abb. 2: Parkettierung
Wir zhlen oben vier
und unten fnf Teildreiecke. Nun ist es so, das die drei grnen und die dazwischen
eingeklemmten roten Teildreiecke ein Sechseck bilden, das bezglich der blauen
Geraden symmetrisch liegt. Problematisch sind also noch die drei roten Dreiecke
au§en, eins oben und zwei unten (Abb. 3).
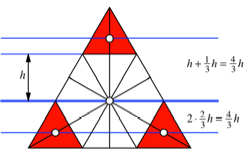
Abb. 3: Hebelgesetze
Nun hat das obere
Dreieck von der Gleichgewichtsachse den Abstand ![]() , die beiden unteren je den Abstand
, die beiden unteren je den Abstand ![]() . Wir haben also unten den halben Abstand, aber die doppelte
Masse. Es kommen die Hebelgesetze von Archimedes zum Tragen.
. Wir haben also unten den halben Abstand, aber die doppelte
Masse. Es kommen die Hebelgesetze von Archimedes zum Tragen.
2
Verschiedene Schwerpunkte
Beim Eckenschwerpunkt denken wir uns gleiche Massen in den Ecken
konzentriert, beim Kantenschwerpunkt
soll die Masse homogen entlang der Kanten oder des Randes verteilt sein (Drahtmodell) und beim Flchenschwerpunkt homogen ber die Flche (Plattenmodell) (Abb. 4).
Die drei Schwerpunkte sind in der Regel voneinander verschieden.

Abb. 4: Ecken-,
Kanten- und Flchenschwerpunkt
Beim Quadrat (Abb. 5
links) ist natrlich alles, was Schwerpunkt hei§t, in der Mitte. Wenn wir nun
aber unten etwas herausbrechen (Abb. 5 rechts), wandert der Flchenschwerpunkt
nach oben und der Kantenschwerpunkt nach unten.

Abb. 5: Verlagerung der
Schwerpunkte?
3
Schwerpunkte beim Dreieck
Beim Dreieck fallen
allerdings der Eckenschwerpunkt und der Flchenschwerpunkt zusammen. Das ist
das, was in der Schule allgemein als ãSchwerpunktÒ bezeichnet wird. Der Kantenschwerpunkt
ist aber im Allgemeinen davon verschieden (siehe unten).
3.1
Der Eckenschwerpunkt ist der Flchenschwerpunkt
Wir beginnen mit einer
Seitenhalbierenden. Diese geht durch eine Ecke, die beiden anderen Ecken sind
gleich weit von der Seitenhalbierenden entfernt. Die Seitenhalbierende ist also
Schwerlinie bezglich der Ecken. Der Eckenschwerpunkt ist der Schnittpunkt von
zwei Schwerlinien. Die Sache mit dem Flchenschwerpunkt beweisen wir mit dem
Prinzip von Cavalieri (Abb. 6). Wir zerschneiden die Dreiecksflche parallel
zur Seitenhalbierenden in (unendlich) dnne Streifen. Streifen mit gleichem
Abstand von der Seitenhalbierenden haben gleiche Lnge. Dies folgt aus
Strahlenstzen. Somit sind diese beiden Streifen bezglich der
Seitenhalbierenden im Gleichgewicht. Die Seitenhalbierende ist daher auch
Schwerlinie bezglich der Ecken. Der Flchenschwerpunkt ist der Schnittpunkt
von zwei Seitenhalbierenden und fllt mit dem Eckenschwerpunkt zusammen.
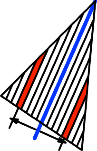
Abb. 6: Prinzip von
Cavalieri
3.2
Die Dreihebelwaage
Eine bekannte
Denksportaufgabe luft unter dem Namen "The Odd Ball Problem". Darin
geht es darum, von zwlf optisch nicht unterscheidbaren Kugeln durch Wgen
mit einer Zweihebel-Waage (Abb. 7) die eine Kugel zu bestimmen, deren Gewicht
vom Gewicht der brigen elf Kugeln abweicht. Man weiss nicht, ob die "odd
ball" schwerer oder leichter ist. Die eigentliche Denksportaufgabe besteht
darin, mit mglichst wenigen Wgungen auszukommen.

Abb. 7: Zweihebel-Waage
Das nahe liegende
Vorgehen besteht darin, die Kugeln in drei Vierergruppen aufzuteilen und zwei
dieser drei Vierergruppen gegeneinander zu wgen. Je nach Ausgang der Wgung
werden die beiden Vierergruppen, die in der nachfolgenden zweiten Wgung gegeneinander
gewogen werden, bestimmt, und so verfhrt man auch fr die dritte Wgung.
Einfacher geht es mit
einer Dreihebel-Waage. Es gibt zwei Konstruktionsmglichkeiten, eine
horizontale und eine vertikale. Physikalisch laufen beide nach demselben
Prinzip.
Der geneigte Leser ist
eingeladen, sich zu berlegen, was ãGleichgewichtÒ bei den beiden Waagentypen
bedeutet.
Horizontale
Dreihebel-Waage: Wir denken uns einen horizontal liegenden Mercedes-Stern, der
in der Mitte in einem Kugelgelenk aufgehngt oder durch ein Nadelgelenk
untersttzt ist. An jeder Sternspitze hngt eine Waagschale (Abb. 8).
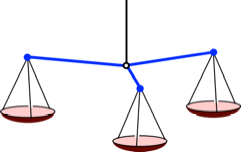
Abb. 8: Horizontale
Dreihebel-Waage
Vertikale
Dreihebel-Waage: Riesenrad mit drei Gondeln (Abb. 9).
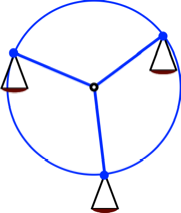
Abb. 9: Riesenrad mit
drei Gondeln
Wir teilen die 12
Kugeln in drei Vierergruppen auf und geben jede Vierergruppe in eine der drei
Waagschalen. Wenn nun eine der Waagschalen unten ist und die beiden anderen
Waagschalen auf gleicher Hhe oben, ist in der unteren Waagschale die ãodd
ballÒ, und sie ist schwerer. Nun nehmen wir drei der vier Kugeln aus der
unteren Waagschale und geben je eine in eine Waagschale. Falls diese im
Gleichgewicht bleiben, ist die vierte Kugel die schwerere, ansonsten ist es die
Kugel in der wiederum unteren Waagschale.
Falls die ãodd ballÒ
leichter ist, geht eine der Waagschalen jeweils nach oben und wir knnen analog
weiterfahren und schlie§en.
Wir kommen also mit
zwei Wgungen aus.
Mit der Dreihebel-Waage
knnen wir das ãodd ball problemÒ fr 48 Kugeln mit 3 Wgungen lsen: wir
teilen die 48 Kugeln in vier Gruppen zu je 12 Kugeln auf und legen je eine
Zwlfergruppe in eine Waagschale. Bei Gleichgewicht ist die faule Kugel in der
vierten Zwlfergruppe und wir knnen wie oben mit zwei weiteren Wgungen weiterfahren.
Bei Ungleichgewicht erhalten wir ebenfalls die Information, in welcher Zwlfergruppe
die faule Kugel ist (inklusive der Zusatzinformation, ob die faule Kugel schwerer
oder leichter ist). Wir knnen auch da wie oben weiterfahren.
Bei ![]() Kugeln reichen n Wgungen mit der Dreihebel-Waage.
Kugeln reichen n Wgungen mit der Dreihebel-Waage.
Ein Parittsproblem: Nun
ist man versucht, eine Waage mit zwlf Waagschalen zu bauen und das ãodd ballÒ
Problem mit einer einzigen Wgung zu lsen. Das geht aber in die Hosen: Wir
wissen dann nicht, ob die unterste Waagschale die ãodd ballÒ als schwerere
Kugel enthlt oder die oberste Waagschale die ãodd ballÒ als leichtere Kugel.
Das liegt daran, dass 12 eine gerade Zahl ist und wir somit paarweise
diametrale Waagschalen haben.
Eine Zwlfhebel-Waage
enthlt eben auch Zweihebel-Waagen, Dreihebel-Waagen, Vierhebel-Waagen und Sechshebel-Waagen.
Man muss einfach die Waagschalen dazwischen leer lassen.
Bei 11 oder allgemein
einer ungeraden Anzahl Kugeln kmen wir mit einer entsprechenden Waage mit
einer Wgung durch, weil wir dann nicht gleichzeitig eine unterste und eine
oberste Waagschale htten.
3.3
Eine Aufgabe zum Eckenschwerpunkt
Einem beliebigen
Dreieck ![]() setzen wir auf
den Seiten drei zueinander hnliche Dreiecke
setzen wir auf
den Seiten drei zueinander hnliche Dreiecke ![]() ,
, ![]() und
und ![]() an (Abb. 10).
Die Dreiecke drfen nach au§en oder nach innen angesetzt werden.
an (Abb. 10).
Die Dreiecke drfen nach au§en oder nach innen angesetzt werden.
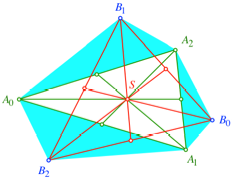
Abb. 10: Ansetzen
hnlicher Dreiecke
Dann haben die beiden
Dreiecke ![]() und
und ![]() denselben
Schwerpunkt S.
denselben
Schwerpunkt S.
Beweis: Wir interpretieren
die Punkte als komplexe Zahlen in der Gau§schen Zahlenebene. Zunchst ist dann:
![]()
Weiter gilt wegen der
hnlichkeit der angesetzten Dreiecke:
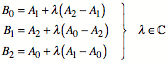
Fr den Schwerpunkt T des Dreieckes ![]() erhalten wir:
erhalten wir:
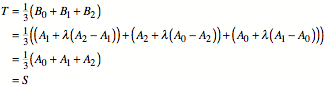
3.4
Der Kantenschwerpunkt
Wir konzentrieren uns
zunchst auf zwei der drei Kanten (Abb. 11).
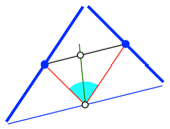
Abb. 11: Zwei der drei
Kanten
Die beiden Kanten haben
je ihren Mittelpunkt als Schwerpunkt. Wir haben nun aber in diesen Punkten
unterschiedliche Massen, da die Kanten ungleich lang sind. Der Schwerpunkt
dieser beiden Kanten muss also so gefunden werden, dass die beteiligten
Hebelarme im umgekehrten Verhltnis zu den Seitenlngen stehen.
Nun sind die beiden
Seitenlngen im selben Verhltnis wie die dazu parallelen Seitenlngen des
Mittendreiecks. Die Winkelhalbierende des Winkels zwischen diesen beiden Seiten
teilt die dritte Seite des Mittendreiecks im gewnschten Verhltnis. Da diese
Winkelhalbierende auch durch den Schwerpunkt (Mittelpunkt) der dritten Seite
geht, ist sie eine Schwerlinie bezglich der Kanten. Der Kantenmittelpunkt ist
daher der Schnittpunkt der drei Winkelhalbierenden des Mittendreieckes, also
dessen Inkreismittelpunkt.
Dieser Punkt ist in der
Regel vom Ecken- und Flchenschwerpunkt verschieden.
Frage: Gibt es au§er
dem gleichseitigen Dreieck noch andere Dreiecke, bei denen der
Kantenschwerpunkt mit dem Eckenschwerpunkt zusammenfllt?
4
Schwerpunkte beim Viereck
4.1
Eckenschwerpunkt
Der Eckenschwerpunkt E eines Vierecks ![]() ergibt sich als
Schnittpunkt der Geraden
ergibt sich als
Schnittpunkt der Geraden ![]() und
und ![]() (Abb. 12). Dabei
ist
(Abb. 12). Dabei
ist ![]() der Mittelpunkt
der Strecke
der Mittelpunkt
der Strecke ![]() . Vorstellung: Wir denken uns eine Mobile mit gleichen Massen
in den Eckpunkten, den Jochen zweiter Ordnung
. Vorstellung: Wir denken uns eine Mobile mit gleichen Massen
in den Eckpunkten, den Jochen zweiter Ordnung ![]() und
und ![]() sowie dem Joch
erster Ordnung
sowie dem Joch
erster Ordnung ![]() . Der Mittelpunkt von
. Der Mittelpunkt von ![]() ist der
Aufhngepunkt des Mobile, also der Eckenschwerpunkt. Diesen erhalten wir aber
auch ber das Mobile mit den Jochen
ist der
Aufhngepunkt des Mobile, also der Eckenschwerpunkt. Diesen erhalten wir aber
auch ber das Mobile mit den Jochen ![]() und
und ![]() sowie dem Joch
sowie dem Joch ![]() . Der Schnittpunkt der beiden Joche ersten Grades ist also
der Eckenschwerpunkt E.
. Der Schnittpunkt der beiden Joche ersten Grades ist also
der Eckenschwerpunkt E.
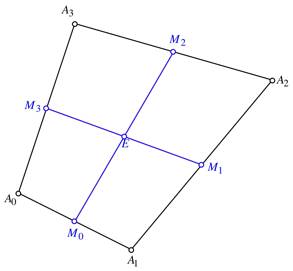
Abb. 12:
Eckenschwerpunkt
Frage: Wie verhlt sich
die Verbindungsstrecke der Mittelpunkte der beiden Diagonalen ![]() und
und ![]() ?
?
Frage: Wie finden wir
den Eckenschwerpunkt eines allgemeinen Tetraeders?
4.2
Flchenschwerpunkt
Den Flchenschwerpunkt F finden wir ebenfalls mit einer Mobile-berlegung.
Mit einer Diagonale teilen wir das Viereck in zwei Dreiecke und verjochen dann
deren Flchenschwerpunkte. Im Dreieck ist aber der Flchenschwerpunkt gleich
dem Eckenschwerpunkt. Zunchst zeichnen wir den Stern der Abbildung 13.
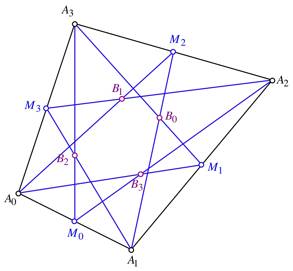
Abb. 13: Stern
Der in der Abbildung 13
eingezeichnete Punkt ![]() ist der
Schwerpunkt des Dreiecks
ist der
Schwerpunkt des Dreiecks ![]() . Entsprechend fr die anderen Punkte
. Entsprechend fr die anderen Punkte ![]() . Daher ist der Schnittpunkt der Joche
. Daher ist der Schnittpunkt der Joche ![]() und
und ![]() der
Flchenschwerpunkt F (Abb. 14).
der
Flchenschwerpunkt F (Abb. 14).
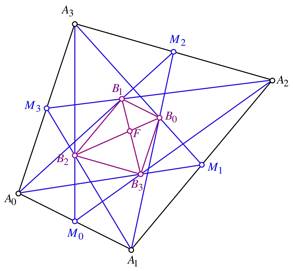
Abb. 14:
Flchenschwerpunkt
Der Flchenschwerpunkt F ist also der Diagonalenschnittpunkt des Viereckes ![]() . Dieses Viereck hat es in sich. So ist zum Beispiel die
Seite
. Dieses Viereck hat es in sich. So ist zum Beispiel die
Seite ![]() parallel zur
Seite
parallel zur
Seite ![]() und ein Drittel
so lang. Diese folgt aus der Teilungseigenschaft 1:2 des Dreiecksschwerpunktes
sowie Strahlenstzen. Das Viereck
und ein Drittel
so lang. Diese folgt aus der Teilungseigenschaft 1:2 des Dreiecksschwerpunktes
sowie Strahlenstzen. Das Viereck ![]() ist also das
Bild des Ausgangsvierecks
ist also das
Bild des Ausgangsvierecks ![]() bei einer
zentrischen Streckung mit dem Faktor
bei einer
zentrischen Streckung mit dem Faktor ![]() . Bei dieser Streckung wir der Diagonalenschnittpunkt D des Vierecks
. Bei dieser Streckung wir der Diagonalenschnittpunkt D des Vierecks ![]() auf den
Flchenschwerpunkt F abgebildet.
Das Zentrum der Streckung teilt also die Strecke DF innen im Verhltnis 3:1.
auf den
Flchenschwerpunkt F abgebildet.
Das Zentrum der Streckung teilt also die Strecke DF innen im Verhltnis 3:1.
Der Mittelpunkt ![]() der Strecke
der Strecke ![]() liegt auf der
Geraden
liegt auf der
Geraden ![]() (Strahlenstze)
und wird bei der zentrischen Streckung auf den Punkt
(Strahlenstze)
und wird bei der zentrischen Streckung auf den Punkt ![]() abgebildet. Das
Zentrum der Streckung liegt also auf der Geraden
abgebildet. Das
Zentrum der Streckung liegt also auf der Geraden ![]() . Ebenso liegt das Zentrum auf der Geraden
. Ebenso liegt das Zentrum auf der Geraden ![]() . Das Zentrum der Streckung ist daher der Eckenschwerpunkt E. Somit haben wir den Sachverhalt:
. Das Zentrum der Streckung ist daher der Eckenschwerpunkt E. Somit haben wir den Sachverhalt:
Im allgemeinen Viereck
liegen der Diagonalenschnittpunkt D, der
Eckenschwerpunkt E und der
Flchenschwerpunkt F auf einer
Geraden. Der Punkt E teilt die
Strecke DF im Verhltnis 3:1
(Abb. 15).
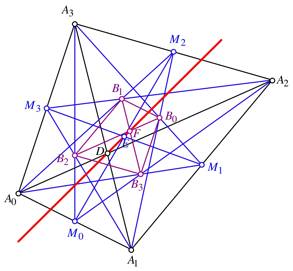
Abb. 15: Die Gerade
Der Kantenschwerpunkt
liegt nicht auf dieser Geraden.
ber Vierecke, in denen
Kanten- und Flchenschwerpunkt bereinstimmen, siehe [Meixner / Metsch 2004].
Frage: Wie lsst sich
die Schnittpunkteigenschaft der Abbildung 16 erklren?
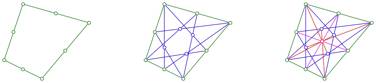
Abb. 16: Ein Schnittpunkt
4.3 Anstze zur Parkettierung
Spiegeln des Vierecks ![]() an den
Mittelpunkten der Seiten des Vierecks fhrt zu einer Beinahe-Parkettierung
(Abb. 17). Die Spiegelbilder sitzen passgenau. An den Ecken des
Ausgangsvierecks
an den
Mittelpunkten der Seiten des Vierecks fhrt zu einer Beinahe-Parkettierung
(Abb. 17). Die Spiegelbilder sitzen passgenau. An den Ecken des
Ausgangsvierecks ![]() entstehen
unterschiedlich gro§e Parallelogramme.
entstehen
unterschiedlich gro§e Parallelogramme.
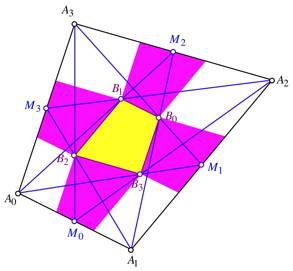
Abb. 17: Unterteilung des Vierecks
4.4
Eine Aufgabe zum Eckenschwerpunkt
Einem beliebigen
Viereck ![]() setzen wir auf
den Seiten vier zueinander hnliche Dreiecke
setzen wir auf
den Seiten vier zueinander hnliche Dreiecke ![]() ,
, ![]() ,
, ![]() und
und ![]() an (Abb. 18).
Die Dreiecke drfen nach au§en oder nach innen angesetzt werden.
an (Abb. 18).
Die Dreiecke drfen nach au§en oder nach innen angesetzt werden.
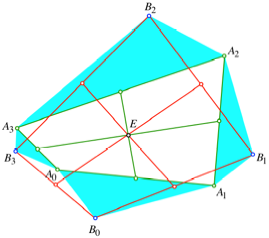
Abb. 18: Ansetzen von
Dreiecken
Dann haben die beiden
Vierecke ![]() und
und ![]() denselben
Eckenschwerpunkt E.
denselben
Eckenschwerpunkt E.
Frage: Wie lsst sich
das beweisen?
Frage: Gibt es eine
Verallgemeinerungsmglichkeit?
4.5
Ein merkwrdiges Viereck
In einem beliebigen
Dreieck ABC zeichnen wir den
Inkreismittelpunkt ![]() und die drei
Ankreismittelpunkte
und die drei
Ankreismittelpunkte ![]() (Abb. 19). So
entsteht ein nicht konvexes Viereck
(Abb. 19). So
entsteht ein nicht konvexes Viereck ![]() .
.
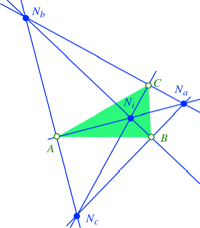
Abb. 19: Ein Viereck im
Dreieck
Dann ist der
Eckenschwerpunkt des Viereckes ![]() der
Umkreismittelpunkt U des Dreiecks ABC
(Abb. 20).
der
Umkreismittelpunkt U des Dreiecks ABC
(Abb. 20).
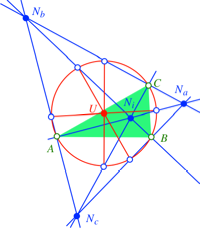
Abb. 20: Umkreis des
Dreiecks
Beweisskizze: Die
inneren und u§eren Winkelhalbierenden des Dreieckes ABC bilden ein Dreieck ![]() mit
Hhenschnittpunkt
mit
Hhenschnittpunkt ![]() . Der Umkreis des Dreiecks ABC ist der Feuerbachkreis des Dreiecks
. Der Umkreis des Dreiecks ABC ist der Feuerbachkreis des Dreiecks ![]() . Die Mittelpunkte der Strecken
. Die Mittelpunkte der Strecken ![]() ,
, ![]() und
und ![]() respektive der
Strecken
respektive der
Strecken ![]() ,
, ![]() , und
, und ![]() liegen diametral
auf dem Feuerbachkreis. Daraus ergibt sich die Behauptung.
liegen diametral
auf dem Feuerbachkreis. Daraus ergibt sich die Behauptung.
Literatur
[Meixner / Metsch 2004] Meixner, T. / Metsch, K.: ber Vierecke, in denen Kanten- und Flchenschwerpunkt bereinstimmen. Math. Semesterber. 51, (2004) S. 131-145.
Hans Walser
Mathematisches Institut
Universitt Basel
Rheinsprung 21
CH 4051 Basel
Tel. +4161 267 26 87
hwalser at bluewin dot ch