Hans Walser
Arbeitskreis Geometrie
Herbsttagung 14. – 16. September 2012, Saarbrcken
Tagungsthema: Begriffsbilden im Geometrieunterricht
Vergessene Vierecke
Zusammenfassung
Es werden drei Vierecke vorgestellt, die im
blichen Begriffskanon, etwa dem Haus der Vierecke,
offenbar vergessen worden sind. Sie haben nicht einmal einen Namen. Eines der
drei Vierecke hat Beziehungen zu Pythagoras (Quadratsummen), Briefumschlgen,
Faltgeometrie und Wegoptimierung im Viereck.
1
Drei Fragen und eine Lehrerfrage
á
Aus welchen Vierecken lsst sich ein
Briefumschlag falten?
á
In welchem Viereck ist ![]() ?
?
á
In
welchem Viereck hat es zwei gleich lange optimale Wegenetze? (Abb.1)
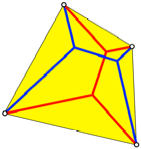
Abb. 1:
rot = blau?
á
Lehrerfrage:
In welchem Viereck sind die beiden Mittenlinien gleich lang?
2
Klassische Beispiele von Begriffssystemen
á
Ein Viereck ist ein Viereck ist ein
Viereck: Das Haus der
Vierecke zur Begriffsbildung
und als Kanon? — Es kann bei Schlerinnen und Schlern den Anschein einer
vollstndigen bersicht erwecken, eines Kanons, au§erhalb desselben nicht mehr
zulssig ist.
á
Carl von Linn: Systema naturae
á
Mendelejew: Periodensystem
á
IUC notation: Bandornamente
á
Benjamin Samuel Bloom: Lernzieltaxonometrie
Begriffssysteme
sollten erst eingefhrt werden, wenn sie sich von der Sache her aufdrngen.
3
Kindersprache und Schulsprache
Kindersprache:
Viereck, Langeck
Schulsprache:
Quadrat, Rechteck
Kindersprache:
Dornrschen, Stachelbeeren
Schulsprache:
Die Rosen haben Stacheln, die Stachelbeerbsche haben Dornen.
4
Orthogonale Diagonalen
Das
Viereck mit orthogonalen Diagonalen ist die allgemeine Lsung zu den Eingangsfragen.
4.1
Mittenlinien
Bei einem
beliebigen Viereck ist das Seitenmittenviereck ein Parallelogramm, dessen
Seiten parallel zu den Diagonalen liegen. Die Mittenlinien sind die Diagonalen
dieses Parallelogramms.
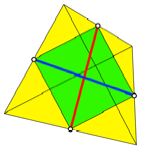
Abb. 2:
Seitenmittenparallelogramm ein Rechteck
Genau bei
orthogonalen Diagonalen ist das Seitenmittenparallelogramm ein Rechteck und
seine Diagonalen sind gleich lang (Abb. 2).
In diesem
Fall ist der Flcheninhalt des Viereckes das halbe Produkt der beiden Diagonalenlngen.
4.2
Briefumschlag
Aus
welchen Vierecken lsst sich ein Briefumschlag falten?
Sicher geht es bei einem Rhombus: Wenn wir die vier Ecken in die Mitte einfalten, entsteht ein Briefumschlag (von den Klebefalzen wird abgesehen).
Gibt es
andere Papier-Vierecke, mit denen sich berlappungsfrei und lckenlos ein
Briefumschlag herstellen lsst?
Ist dies
insbesondere mit einem Rechteck mglich?
Jedenfalls
knnen wir einen Briefumschlag falten, wenn die Diagonalen des ursprnglichen
Papier-Viereckes orthogonal sind (Abb. 3). Der Umriss des Briefumschlages ist
das Kantenmittenrechteck.
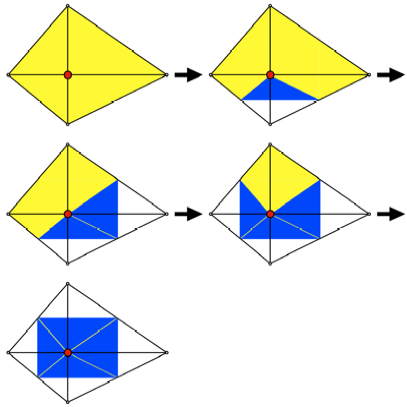
Abb. 3:
Viereck mit orthogonalen Diagonalen
Die Ecken
des Papier-Viereckes kommen im Diagonalenschnittpunkt zusammen. Geht es auch,
wenn die Diagonalen nicht orthogonal sind?
4.3
Alternierende Quadratsumme
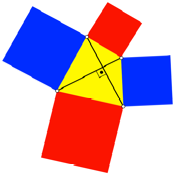
Abb. 4:
rot = blau
Bei
orthogonalen Diagonalen ergeben sich im Viereck vier rechtwinklige Dreiecke.
Bei alternierender Anwendung des Satzes von Pythagoras neutralisieren sich die
Kathetenquadrate.
4.4 Wegenetze im Viereck
Wir
treffen die etwas naive Annahme, dass der Ausbaustandard unabhngig vom (erwarteten)
Verkehrsaufkommen ist. Die grne Verbindungsstrecke zwischen den beiden
Verzweigungspunkten (Abb. 5) soll also gleich wie die anderen Strecken gebaut
werden, obwohl es sinnvoll wre, diesen Flaschenhals etwas breiter (und zur
Kostonoptimierung etwas krzer) zu bauen.
4.4.1 Beliebige Wegenetze
Wie kann die gesamte Lnge eines beliebigen Wegenetzes (Abb. 5) in einem allgemeinen Viereck visualisiert werden?
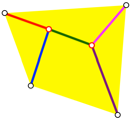
Abb. 5: Wegenetz im Viereck
Der Trick (oder ist es eine Methode?) besteht darin, geeignete Dreiecke um 60¡ herauszudrehen (Abb. 6). Dadurch entsteht ein Polygonzug, der gleich lang ist wie das gesamte Wegenetz. Die Endpunkte dieses Polygonzuges sind Ecken von nach au§en angesetzten gleichseitigen Dreiecken.
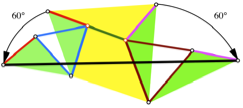
Abb. 6: Gesamtlnge
und minimale Gesamtlnge
Diese
Endpunkte sind - bei gegebener Netztopologie - invariant; die Minimallnge des
gesamten Netzes ergibt sich daher durch die Strecke, welche diese Endpunkte
verbindet (Abb. 7).
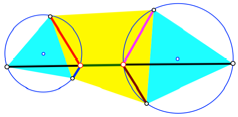
Abb. 7: Verzweigungspunkte
Die Verzweigungspunkte finden sich dann durch die Umkreise der beiden gleichseitigen Dreiecke, welche auch Ortsbogen fr 120¡ sind.
4.4.2 Die zweite Lsung
Wenn wir die beiden gleichseitigen Dreiecke an den anderen beiden Vierecksseiten aufsetzen, ergibt sich eine zweite Lsung mit einer anderen Netztopologie. Dieses Netz hat in der Regel eine andere Gesamtlnge. Unsere Konstruktionen liefern also nicht in jedem Fall das Minimalnetz, sondern allenfalls blo§ ein relatives Minimalnetz, das hei§t das Minimalnetz bei gegebener Netztopologie.
4.4.3
Welche Lsung ist die bessere?
Zur
Klrung der Frage, welche der beiden Lsungen die bessere ist, gengt es
offenbar, an den Vierecksseiten gleichseitige Dreiecke anzusetzen und die Verbindungen
gegenberliegender Au§enspitzen zur vergleichen (Abb. 8).
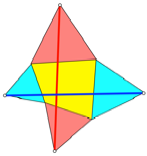
Abb. 8:
rot = blau?
Mehr dazu
im folgenden Abschnitt.
4.5
Ansetzen von hnlichen gleichschenkligen
Dreiecken
Wir
bearbeiten einen allgemeinen Fall, indem wir den Seiten eines beliebigen Vierecks
hnliche gleichschenklige Dreiecke ansetzen, und suchen dann einen Zusammenhang
zwischen der roten und der blauen Strecke.
Wir
verwenden die Vektoren und Bezeichnungen der Abbildung 9.
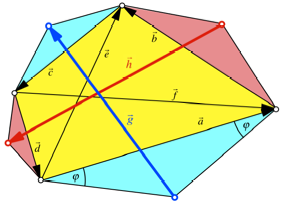
Abb. 9:
Ansetzen von gleichschenkligen Dreiecken
Die
gleichschenkligen Dreiecke haben den Basiswinkel ![]() . Fr positives
. Fr positives ![]() sind die
gleichschenkligen Dreiecke au§en anzusetzen, fr negatives
sind die
gleichschenkligen Dreiecke au§en anzusetzen, fr negatives ![]() innen. Fr
innen. Fr ![]() sind die rote
und die blaue Strecke Verbindungslinien gegenberliegender Seitenmitten des
Vierecks.
sind die rote
und die blaue Strecke Verbindungslinien gegenberliegender Seitenmitten des
Vierecks.
Mit
einiger Rechnung finden wir:
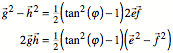
Fr ![]() hei§t das
folgendes:
hei§t das
folgendes:
Genau
wenn die Diagonalen des Viereckes orthogonal sind, haben die rote und die blaue
Strecke die gleiche Lnge.
Genau
wenn die Diagonalen des Viereckes gleich lang sind, stehen die rote und die
blaue Strecke rechtwinklig aufeinander.
4.5.1
Orthogonale Diagonalen
Genau wenn
die Diagonalen des Viereckes orthogonal sind, haben die rote und die blaue
Strecke die gleiche Lnge (Abb. 10). Gem§ dem Abschnitt ber die alternierende
Quadratsumme gilt zudem, dass die Flchensumme der roten gleichschenkligen Dreiecke
gleich der Flchensumme der blauen gleichschenkligen Dreiecke ist.
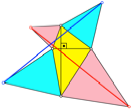
Abb. 10:
rot = blau
Genau in
den Vierecken mit orthogonalen Diagonalen sind also auch die beiden optimalen
Wegenetze gleich lang, was mit ![]() gezeigt werden
kann.
gezeigt werden
kann.
4.5.2
Gleich lange Diagonalen
Genau
wenn die Diagonalen des Viereckes gleich lang sind, stehen die rote und die
blaue Strecke rechtwinklig aufeinander (Abb. 11).
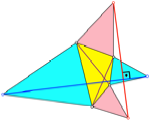
Abb. 11:
rot senkrecht blau
Dies ist
sozusagen die duale Situation zu den Vierecken mit orthogonalen Diagonalen.
5
Der Sonderfall
Wegen
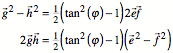
folgt fr
![]() : Bei einem beliebigen Startviereck sind die rote und die
blaue Strecke gleich lang und orthogonal (Abb. 12).
: Bei einem beliebigen Startviereck sind die rote und die
blaue Strecke gleich lang und orthogonal (Abb. 12).
Die
Au§enecken der Figur bilden also ein Viereck mit orthogonalen und gleich langen
Diagonalen. Dies ist ein naher Verwandter des Quadrates.
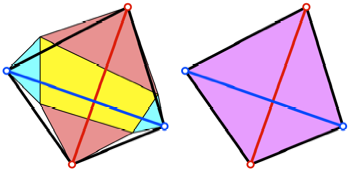
Abb. 12:
Viereck mit orthogonalen und gleich langen Diagonalen
Literatur
[Haag 2003] Haag, Wilfried: Wege zu geometrischen Stzen. Stuttgart: Klett 2003. ISBN 3-12-720120-6