Hans Walser

Das DIN-Format

Lehrerinnen- und Lehrertag

Basel, Mittwoch, 11. Februar 2015

Zusammenfassung

Das DIN-Format ist mehr als ein Stück Papier und die Quadratwurzel aus Zwei. Wir treffen auf Spiralen, Grenzpunkte, die gleichtemperierte 12-Ton-Stimmung, das Silberne Rechteck, Faltprobleme und Legespiele nach Fröbel. Explizit werden Faltaufgaben besprochen, die nur mit einem Papierblatt in einem DIN-Format möglich sind. Insbesondere kommen das regelmäßige Achteck sowie Kantenmodelle von Würfel und Tetraeder zur Sprache.

1 Wurzel aus zwei

Wenn wir ein DIN A4 Papier längs der kurzen Mittellinie falten, ergibt sich ein doppellagiges DIN A5 Papier. Dieses hat nun dieselbe Form (Ähnlichkeit), also dieselben Seitenverhältnisse wie das DIN A4 Papier, wie durch Anlegen an eine gemeinsame Diagonale nachgeprüft werden kann.

DIN A4 und DIN A5

Mit der Schmalseite 1 und der Langseite x für das DIN A4 Rechteck erhalten wir aus der Ähnlichkeit:

Dieses Seitenverhältnis kann durch Falten nachgeprüft werden (Abb. 2). Dabei benützen wir den Sachverhalt, dass im Quadrat die Diagonalen-Länge das der Seitenlänge ausmacht.

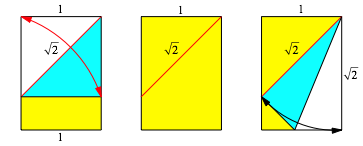
Kontrolle durch Falten

Beim Abschneiden eines Quadrates vom DIN-Rechteck (etwa beim Zuschneiden von Origami-Papier) bleibt ein Rechteck mit dem Seitenverhältnis übrig. Dies ist das so genannte Silberne Rechteck. Es hat ähnliche Eigenschaften wie das Goldene Rechteck (vgl. Walser 2013).

2 Ausschöpfen des A0-Rechteckes

2.1 Die klassische Art

Wir können mit einem Set von DIN-Rechtecken A1, A2, A3, ... ein A0-Rechteck ausschöpfen. Die Rechtecke sind im Wechsel im Quer- und Hochformat.

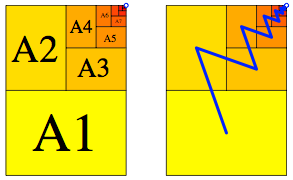
Ausschöpfung des A0-Rechteckes

Wenn wir die Mitten aufeinanderfolgender Rechtecke verbinden, ergibt sich eine Zickzack-Linie, welche in den Grenzpunkt rechts oben mündet.

2.2 Spiralförmige Anordnung

Wir können das Set von Rechtecken A1, A2, A3, ... aber auch spiralförmig anordnen.

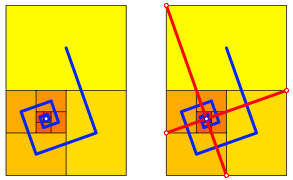
Spiralförmige Anordnung

Der Grenzpunkt ergibt sich durch Einzeichnen geeigneter Halbdiagonalen.

Der Grenzpunkt hat „Drittelkoordinaten“.

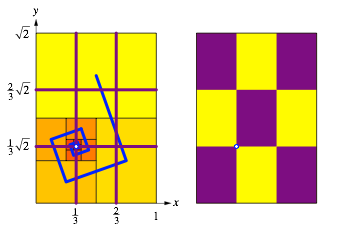
Drittel bei den Koordinaten

Das kann wie folgt eingesehen werden: Wenn auf der Höhe des Grenzpunktes von links her einfahren, treffen wir nur Hochformat-Rechtecke, und zwar der Reihe nach A4, A8, A12, A16, ... . Diese haben im angegebenen Koordinatensystem die Breiten , , , , ... . Für die x-Koordinate des Grenzpunktes ergibt sich daher die geometrische Reihe:

Ein violettes Rechteck hat das Seitenverhältnis des DIN-Formates. Es bedeckt einen Neuntel des A0-Rechteks. Welchen DIN-Code hat es?

Dazu vergleichen wir mit den Flächenanteilen im DIN-System.

Wir sehen, dass unser violettes Rechteck zwischen A3 und A4 liegt, gefühlsmäßig näher an A3. Rechnerisch erhalten wir:

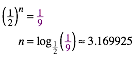
3 Historisches

Wilhelm Ostwald (1853-1932). Walter Porstmann (1886-1959)

3.1 Wilhelm Ostwald

Der Nobelpreisträger Wilhelm Ostwald (1853-1932, Nobelpreis für Chemie 1909, entwickelte 1911 ein System von Papierformaten, das er als Weltformat bezeichnete (Ostwald 1911). Geometrische Grundlage ist das Rechteck mit dem Seitenverhältnis , also wie beim heutigen DIN-Rechteck. Das System wurde längenmäßig auf das metrische System bezogen, indem das kleinste Rechteck (Weltformat I) die kurze Seite 1cm aufwies.

3.2 Walter Porstmann

Der Ingenieur, Mathematiker und Normungstheoretiker Walter Porstmann (1886-1959, war zeitweise Assistent von Wilhelm Ostwald. Er engagierte sich für ein System, das nicht längenmäßig, sondern flächenmäßig mit dem metrischen System verbunden ist, also . So entstand das heute noch verwendete DIN-System.

4 Die DIN-Idee. Andere Figuren

Gibt es andere Figuren, die in zwei kongruente, zur Ausgangsfigur ähnliche Teilfiguren zerlegbar sind?

Die Frage ist allgemein gehalten, es ist nicht von Halbieren die Rede, sondern nur von Zerlegen.

4.1 DIN-Parallelogramm

Wir können die DIN-Rechtecke zu Parallelogrammen verscheren.

Parallelogramme

Die Teilparallelogramme sind ungleichsinnig ähnlich zum Startparallelogramm.

4.2 Das rechtwinklig-gleichschenklige Dreieck

Das naheliegende Beispiel ist das rechtwinklig-gleichschenklige Dreieck.

Das rechtwinklig-gleichschenklige Dreieck

Es gibt im rechtwinklig-gleichschenkligen Dreieck ebenfalls eine spiralförmige Anordnung. Der Grenzpunkt führt zu Fünfteln.

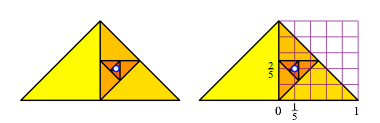
Spiralförmige Anordnung

Die Figur kann auch aus einem halben Origami Papier durch fortlaufendes Falten erreicht werden.

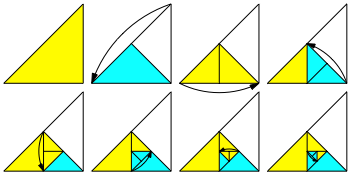
Faltprozess

Faltmodell

Die Thaleskreise der Teildreiecke verlaufen durch den Grenzpunkt, ebenso eine Auswahl von Seitenhalbierenden.

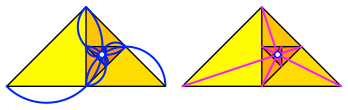
Thaleskreise. Seitenhalbierende

4.3 Sprung in den Raum

4.3.1 DIN-Quader

Wird ein Quader mit dem Kantenverhältnis halbiert, ergeben sich zwei Quader mit dem Kantenverhältnis . Diese sind ähnlich zum ursprünglichen Quader. Die folgende Abbildung zeigt einen DIN-Quader mit dem Kantenverhältnis im Vergleich zum Einheitswürfel.

Die folgende Abbildung zeigt eine Anordnung eines DIN-Quader-Sets analog zur klassischen Anordnung eines Sets von DIN-Rechtecken.

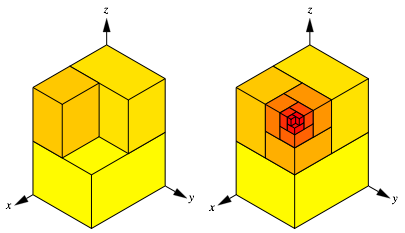
Anordnung

Während bei Rechtecken nur zwischen Querformat und Hochformat unterschieden werden kann, brauchen wir hier drei Anaordnungsformate. Dazu dient das beigefügte Koordinatensystem. Der erste Quader hat seine längsten Kanten in der x-Richtung, der zweite Quader hat seine längsten Kante in der y-Richtung und der dritte Quader in der z-Richtung. Der vierte Quader hat seine längsten Kanten wiederum in der x-Richtung.

Als Stimmungsbild reale DIN-Quader.

DIN-Kisten

4.3.2 DIN-Hyperquader

Im vierdimensionalen Raum ergeben sich durch

oder in anderer Schreibweise

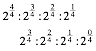
die Kanten zweier aufeinanderfolgender 4d-DIN-Hyperquader. George Pólya (1887-1985) hätte in dieser Situation allerdings von einer Verallgemeinerung durch Verwässerung gesprochen.

4.3.3 Gleichtemperierte 12-Ton-Stimmung

Wir verwässern weiter zum 12d-DIN-Hyperquader.

Das haben wir zwar noch nie gesehen, aber schon gehört. Es sind die Frequenzverhältnisse der Gleichtemperierte 12-Ton-Stimmung.

5 Das Silberne Rechteck

5.1 Ansetzen oder Abschneiden

Wir können zu einem DIN-Rechteck an der Schmalseite ein Quadrat ansetzen oder von einem DIN-Rechteck ein Quadrat abschneiden.

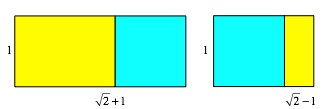
Quadrat ansetzen oder Quadrat abschneiden

Die folgende Abbildung zeigt das Summen- und das Differenzrechteck.

Summenrechteck und Differenzrechteck

Wir erhalten ein Summenrechteck mit dem Seitenverhältnis beziehungsweise ein Differenzrechteck mit dem Seitenverhältnis .

Wegen haben diese beiden Rechtecke dasselbe Seitenverhältnis. Ein solches Rechteck wird mit dem leicht esoterischen Namen Silbernes Rechteck bezeichnet, da es einige Eigenschaften ähnlich denen des Goldenen Rechtecks mit dem Seitenverhältnis des Goldenen Schnittes hat. Über den Goldenen Schnitt siehe (Walser 2013).

5.2 Eigenschaften des Silbernen Rechtecks

Wir können zum Beispiel vom Silbernen Rechteck zwei Quadrate abschneiden, und dann bleibt ein Silbernes Restrechteck übrig.

Zwei Quadrate abschneiden

Der Prozess kann iteriert werden, theoretisch ad infinitum.

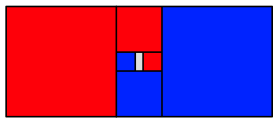
Iteration des Abschneidens

Wir können die Quadrate mit Viertelkreisen füllen. So entstehen zwei Spiralen.

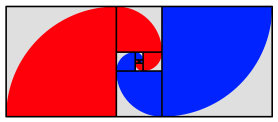
Spiralen

Wir können vier rechtwinklige-gleichschenklige Dreiecke so auslegen, dass ein Silbernes Umrissrechteck und ein Silbernes Lochrechteck entstehen.

Silberne Rechtecke als Umriss und als Loch

Auch dies kann iteriert werden.

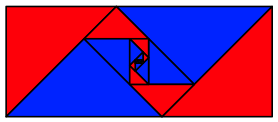
Iteration

5.3 Diagonalenschnittwinkel im Silbernen Rechteck

Die folgende Abbildung zeigt einen Beweis ohne Worte für den Diagonalenschnittwinkel 45° im Silbernen Rechteck. Den Beweis verdanke ich Renato Pandi.

Diagonalenschnittwinkel im Silbernen Rechteck

Der 45°-Winkel ist auch der Zentriwinkel im regelmäßigen Achteck.

6 Das regelmäßige Achteck

Das Silberne Rechteck erscheint im regelmäßigen Achteck.

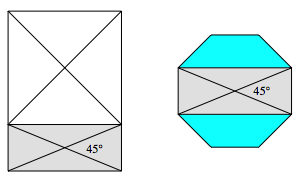
Silbernes Rechteck im regelmäßigen Achteck

Flächenmäßig macht das Silberne Rechteck genau die Hälfte des Achtecks aus. Dies kann mit einem Zerlegungsbeweis eingesehen werden.

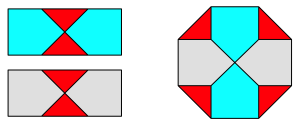
Zerlegungsbeweis

Der Zerlegungsbeweis kann noch subtiler gemacht werden, so dass ein Stern erscheint.

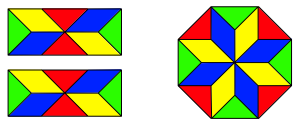
Zerlegungsbeweis mit Stern

Das erinnert an die Legespiele nach Fröbel.

Legespiel nach Fröbel

Mit denselben Bauteilen können auch zwei flächenmäßig halb so große Achtecke ausgelegt werden.

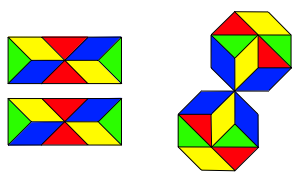
Zwei Achtecke

Wenn wir beim Stern zusätzlich zwei rechtwinklig gleichschenklige Dreiecke ansetzen passt die Figur in ein DIN-Rechteck.

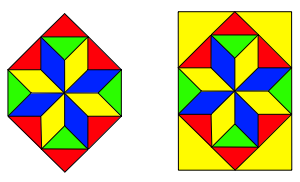
Einpassen ins DIN-Rechteck

Auf Grund dieser Figur kann aus einem DIN-Rechteck ein regelmäßiges Achteck durch Falten hergestellt werden.

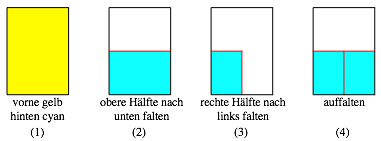
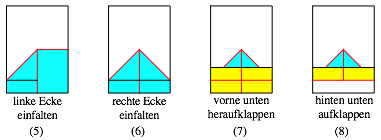
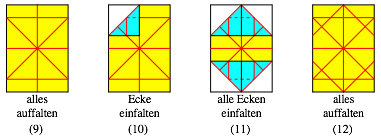
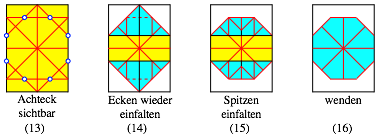
Falten eines Achteckes

7 Würfel und Tetraeder

7.1 Kantenmodell des Würfels

Als Baumaterial dient Papier im DIN A6-Format. Geeignet ist Papier der Stärke 80 g/m², das vom Format A4 auf A6 zugeschnitten wird. Ebenfalls geht es mit dünnen Karteikarten.

Für jede Kante braucht es ein Papier.

Für den Faltprozess verwenden wir eine etwas festere A6-Karte als Faltlehre. Wir legen diese Faltlehre diagonal auf ein A6-Papier und falten die vorstehenden Ecken des darunterliegenden Papiers nach vorne über die Faltlehre. Dann entfernen wir die Faltlehre. Der Umriss des Papiers ist nun ein Rhombus mit dem spitzen Winkel .

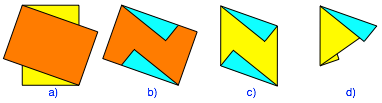
Faltvorgang

Nun falten wir die untere Spitze des Rhombus nach hinten unter die obere Spitze. Diese letzte Faltlinie wird zu einer Kante des Würfels. Was an dieser Kante noch vorsteht, kann zurückgebogen oder abgeschnitten werden. Damit haben wir unser Bauteil. Es hat die Form eines doppellagigen gleichschenkligen Dreiecks mit zwei Verbindungslaschen zum Einschieben in die Nachbarteile.

Die folgende Abbildung zeigt ein geöffnetes Bauteil von innen. Die Spitzen der beiden Rhomben-Hälften müssen vor dem Zusammenbau des Modells noch aufeinander gelegt werden. Diese Spitzen kommen alle in den Mittelpunkt des Würfels zu liegen. Die Seiten der Rhomben werden zu halben Raumdiagonalen des Würfels.

Wir benötigen 12 Bauteile. Beginnend mit drei verschieden farbigen A4-Papieren, die wir zu A6-Papieren vierteln, erhalten wir drei Sätze von je vier gleichfarbigen Bauteilen. Damit können wir den jeweils vier parallelen Würfelkanten dieselbe Farbe zuordnen.

Bauteil

Und nun kommt das Interessante, der Zusammenbau. Wir schieben jeweils eine Verbindungslasche zwischen die beiden gleichschenkligen Dreiecke des Nachbarbauteils. Dabei achten wir darauf, dass an jeder halben Raumdiagonale des Würfels drei Bauteile in den drei verschiedenen Farben zusammen kommen. Parallele Würfelkanten haben dieselbe Farbe.

Kantenmodell des Würfels

Es empfiehlt sich, den Zusammenbau schrittweise mit Büroklammern zu fixieren. An jeder Ecke des Würfels ergeben sich schließlich drei Büroklammern.

Wenn alles sitzt, können die Büroklammern schrittweise entfernt und durch eine Heftklammer mit dem Tacker ersetzt werden. Dabei hat man den Ehrgeiz, dass die Klammern symmetrisch eingebracht werden.

7.2 Kantenmodell des Tetraeders

Beim regelmäßigen Tetraeder haben wir den Ergänzungswinkel von auf 180°, also 109.4712°, als Winkel zwischen den vom Zentrum aus zu den Ecken verlaufenden Strecken. Daher kann analog zum Kantenmodell des Würfels ein Kantenmodell des Tetraeders gebaut werden.

Kantenmodell des Tetraeders

Literatur

Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.