Hans Walser

Maßstab 1:1

Tag der Mathematik

Karl-Franzens-Universität Graz

Donnerstag, 5. Februar 2015

Zusammenfassung

Es werden exemplarisch geometrische Beispiele aus der Ausbildung Studierender in Geomatik, Kartografie, Vermessungswesen und Geografie vorgestellt. Viele Beispiele mit räumlichen und sphärischen Überlegungen sind für Schulunterricht und Begabtenförderung geeignet.

1 Längen oder Winkel?

1.1 Die Mutter aller Karten

Werden geografische Länge und Breite als geometrische Längen in einem kartesischen Koordinatensystem abgetragen, ergibt sich die so genannte Plattkarte. Diese Technik soll auf die Phönizier zurückgehen. Die Abbildung 1 zeigt die heute bekannte Welt in der Plattkarte.

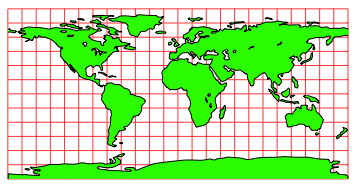
Abb. 1: Plattkarte

1.2 Parameterdarstellung der Kugel

Die Abbildung 2 illustriert die einfachste Parameterdarstellung der Einheitskugel. Hier erscheinen geografische Länge und Breite als Winkel.

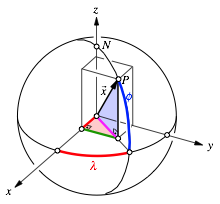
Abb. 2: Parameterdarstellung der Kugel

Wir erhalten mit in kartesischen Koordinaten:

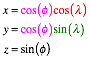
Oder vektoriell:

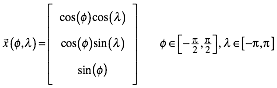
Der Parameterbereich entspricht der Plattkarte (Abb. 3).

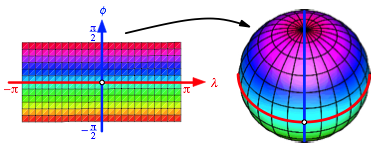
Abb. 3: Plattkarte als Parameterbereich

In der Abbildung 4 sind die Umrisse der Kontinente eingetragen.

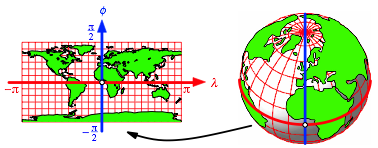
Abb. 4: Plattkarte

Für die Kartografen geht die Überlegung natürlich nicht von links nach rechts, sondern umgekehrt von rechts nach links, von der Realität zur Karte.

Jede Parametrisierung der Kugel, und es gibt deren viele, liefert eine Karte, wenn der Parameterbereich mit den geografischen Daten gefüllt wird.

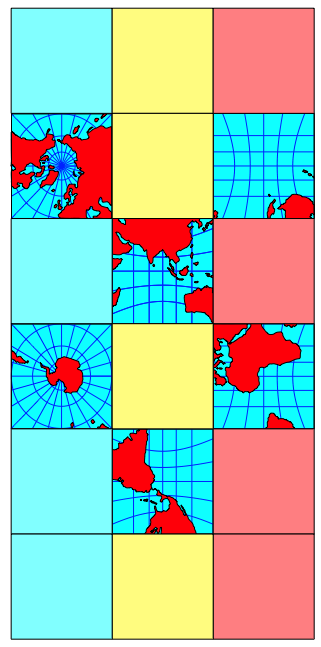
1.3 Plattkarte im Hochformat

Frage eines Studierenden: Können wir in der Parameterdarstellung die Ausmaße des Parameterrechteckes vertauschen? Wir arbeiten dann mit der Parameterdarstellung:

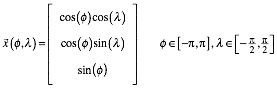
Das Parameterrechteck ist jetzt im Hochformat statt im Querformat.

Nun, zunächst ändert sich gar nichts; ein Computer zeichnet von den Farben abgesehen genau dieselbe Kugel wie vorhin (Abb. 5).

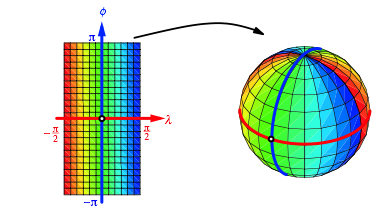
Abb. 5: Parameterrechteck Hochformat

Und nun stellt sich die Frage: Wie sind die äußeren Teile der üblichen Plattkarte abzuschneiden und neu anzusetzen, damit sich die dem Hochformat entsprechende Karte ergibt (Abb. 6)?

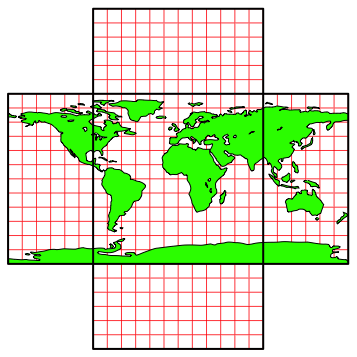
Abb. 6: Abschneiden und Ansetzen?

Antwort: Die vier Teile müssen spiegelbildlich angesetzt werden (Abb. 7). Um das einzusehen, überlege man sich, wie sich die Meridiane auf der „Vorderseite“ (eurozentrisch gedacht) über die Pole hinaus auf die „Rückseite“ fortsetzen. Aus dem Meridian für 30°E wird der Meridian für 150°W. Die Meridiane überkreuzen sich in den Polen.

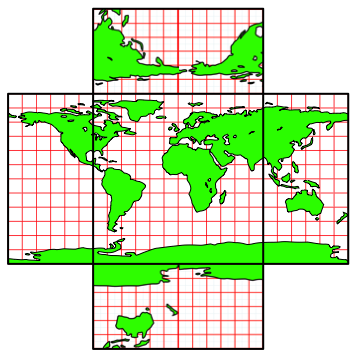
Abb. 7: Ansetzen

Die Abbildung 8 zeigt die Welt im Hochformat.

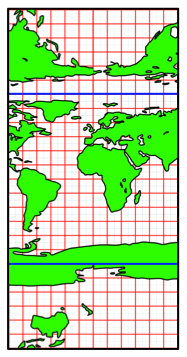
Abb. 8: Die Welt im Hochformat

Wenn wir die Karte auf den Kopf stellen und den Pazifik studieren, stellen wir fest, dass sich beispielsweise Japan und Kalifornien je auf der „falschen“ Seite befinden. Spiegelbildliche Karten sind für uns ungewohnt; falsch sind sie aber nicht. Das Beispiel illustriert vielmehr, wie sehr wir uns an bestimmte Standards in der Kartendisposition gewöhnt haben.

2 Immer gerade aus

2.1 Geodätische Linien

... so geh hübsch sittsam und lauf nicht vom Wege ab!

Abb. 9: Immer der Nase nach

Eine geodätische Linie ist eine Kurve auf einer Oberfläche, bei der subjektiv immer geradeaus gefahren wird. Sie hat also keine Seitenkrümmung nach links oder rechts. Auf der Ebene sind die geodätischen Linien natürlich die üblichen Geraden. Auf der Kugel sind es die Großkreise. Geodätische Linien können durch Abrollen eines (schmalen) Streifens approximiert werden.

2.2 Großkreise statt Geraden

Wenn wir uns auf der Kugel subjektiv „gerade aus“ bewegen, bewegen wir uns auf einem Kreis, welcher denselben Radius und denselben Mittelpunkt hat wie die Kugel. Solche Kreise heißen Großkreise oder Orthodromen. Ihre Trägerebene geht durch den Kugelmittelpunkt.

Großkreise spielen eine wichtige Rolle in der sphärischen Geometrie; sie übernehmen die Rolle der Geraden der ebenen Geometrie. Die kürzeste Verbindung zweier Punkte auf der Kugeloberfläche, gemessen auf der Kugeloberfläche (also nicht in einem geradlinigen Tunnel), ist ein Großkreisbogen.

Der Äquator und alle Meridiane sind Großkreise, nicht aber die übrigen Breitenkreise, welche so genannte Kleinkreise sind. Es gibt aber auch „schräge“ Großkreise, welche den Äquator in einem Winkel schneiden. Die Abbildung 10 zeigt drei solche schräge Großkreise, welche den Äquator unter Winkeln schneiden, in einer allgemeinen Ansicht sowie in einer speziellen Lage mit Sicht von vorne. In dieser speziellen Lage erscheinen die Großkreise als Strecken.

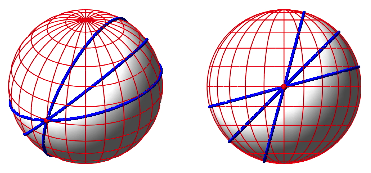
Abb. 10: Großkreise

2.3 Großkreis auf der Plattkarte

Wie sieht der kürzeste Bogen mit den Endpunkten , auf der Plattkarte aus (Abb. 11)?

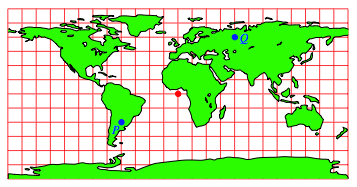
Abb. 11: Kürzeste Verbindung?

Die Abbildung 12 zeigt die Situation auf der Kugel:

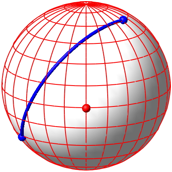
Abb. 12: Situation auf der Kugel

Zunächst ist man versucht, in der Plattkarte eine Strecke von P nach Q einzuzeichnen (Abb. 13).

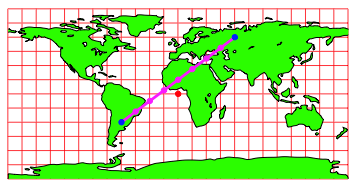
Abb. 13: Ist die Idee richtig?

Das ist aber eine falsche Idee, wie wir durch Abzählen der Netzvierecke einsehen können (Abb. 14).

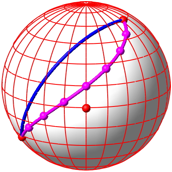
Abb. 14: Eine falsche Idee

Tatsächlich sieht der Großkreisbogen auf der Plattkarte gemäß Abbildung 15 aus:

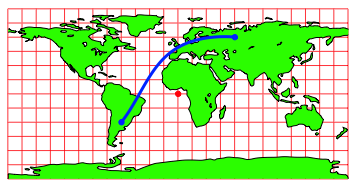
Abb. 15: Großkreisbogen auf Plattkarte

2.4 Großkreise als Geraden auf der Karte?

Auf der Plattkarte erscheinen nur die Meridiane und der Äquator gerade. Die übrigen Großkreise werden gekrümmt dargestellt (Abb. 15).

Gibt es Karten, auf denen alle Großkreise als Geraden erscheinen?

Anekdote: Bei der Planung der Eisenbahn St. Petersburg - Moskau (Nikolaibahn, gebaut 1842 – 1851) wurde lange um die Linienführung gestritten. Zar Nikolaus I. (1825 – 1855) beendete den Streit, indem er auf einer Karte eine gerade Linie zwischen St. Petersburg und Moskau einzeichnete. Ist diese Linienführung optimal?

2.5 Gnomonische Projektion

Die gnomonische Projektion ist eine Zentralprojektion vom Kugelmittelpunkt aus auf eine Tangentialebene. Da Großkreise in einer Ebene durch den Kugelmittelpunkt liegen, ist ihre Projektion die Schnittgerade der Kreisebene mit der Projektionsebene.

2.5.1 Gnomonische Projektion auf die Tangentialebene im Nordpol

In den Abbildungen 16 und 17 wird auf die Tangentialebene im Nordpol projiziert.

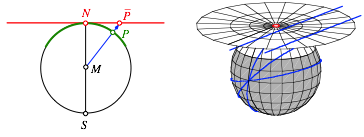
Abb. 16: Tangentialebene im Nordpol

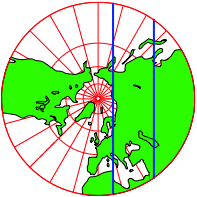
Abb. 17: Gnomonische Projektion

2.5.2 Gnomonische Äquatorialprojektion

Die Abbildung 18 zeigt eine gnomonische Äquatorialprojektion. Die Projektionsebene berührt in einem Äquatorpunkt.

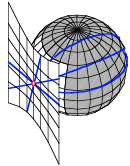
Abb. 18: Gnomonische Äquatorialprojektion

Die Breitenkreise erscheinen in dieser Karte als Hyperbeln (Abb. 19). Warum?

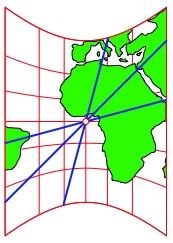
Abb. 19: Gnomonische Äquatorialprojektion

2.5.3 Würfelwelt

Durch Zentralprojektion vom Kugelmittelpunkt aus auf den Umwürfel der Kugel erhalten wir sechs gnomonische Karten.

Im Anhang und auf der Website Würfelwelt ist eine Bastelvorlage mit drei Streifen angegeben aus denen eine Würfelkarte (Abb. 20) geflochten werden kann.

Abb. 20: Flechtwürfel

3 Maßstab eins zu eins

Gibt es eine Karte im Maßstab 1:1 ? — Die Antwort ist ein salomonisches Jein.

Wir arbeiten exemplarisch mit einer Plattkarte von 40 cm Breite und 20 cm Höhe (Abb. 21). Für die Erde nehmen wir eine Kugel mit dem Umfang 40 000 km an.

Am Äquator haben wir daher den Maßstab 1 : 100 000 000, und das gilt in allen Richtungen. Auf den Meridianen haben wir ebenfalls den Maßstab 1 : 100 000 000, aber das gilt nur in der Süd-Nord-Richtung. Weil die Breitenkreise kürzer sind als der Äquator, haben wir auf den Breitenkreisen in West-Ost-Richtung einen größeren Maßstab. Für 60°N ist der Breitenkreis wegen genau halb so lang wie der Äquator, somit haben wir auf diesem Breitenkreis in der West-Ost-Richtung einen doppelt so großen Maßstab, also 1 : 50 000 000.

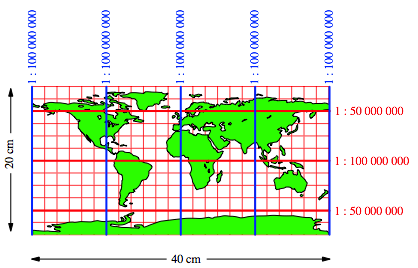
Abb. 21: Maßstäbe

Gegen die Pole zu wird der Maßstab in West-Ost-Richtung immer größer und geht gegen Unendlich. Somit haben wir zwischen dem Äquator und den Polen je eine geografische Breite, auf welcher der Maßstab in West-Ost-Richtung genau 1 : 1 ist.

Das ist allerdings sehr nahe an den Polen. Da die Bilder der Breitenkreise auf unserer Karte die Länge 40 cm haben, suchen wir den Breitenkreis, der in Wirklichkeit den Umfang 40 cm und den Radius 6.37 cm hat. Da an den Polen die Kugel praktisch eben ist, haben wir es mit Kreisen um die Pole mit dem Radius 6.37 cm zu tun.

Zwischen diesen Kreisen und den Polen mit wächst der Maßstab in West-Ost-Richtung von 1 auf Unendlich. In Süd-Nord-Richtung haben wir nach wie vor den Maßstab 1 : 100 000 000.

Auf der Plattkarte sind die Maßstäbe also richtungsabhängig. Zwischen den Extremen mit dem Maximum in West-Ost-Richtung und dem Minimum in Süd-Nord-Richtung variieren die Maßstäbe stetig. Das kann durch eine Ellipse, der so genannten Verzerrungsellipse (Tissotsche Indikatrix), dargestellt werden. Die Abbildung 22 zeigt die Verzerrungsellipsen für die Plattkarte.

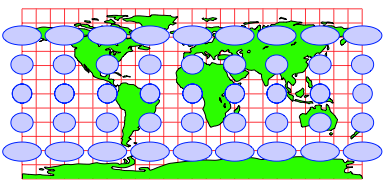
Abb. 22: Verzerrungsellipsen

Die Verzerrungsellipsen kann man sich auch so entstanden denken: Wir bilden einen wirklichen Kreis auf der Erde, zum Beispiel einen runden Swimming Pool, mit ab.

Die Verzerrungsellipsen sind alle gleich hoch, weil wir in der Süd-Nord-Richtung immer denselben Maßstab haben.

In Punkten auf dem Äquator sind die Verzerrungsellipsen Kreise, weil wir dort und nur dort in allen Richtungen denselben Maßstab haben.

Leider gibt es keine Karten, welche in allen Punkten und in allen Richtungen immer denselben Maßstab haben.

4 Das Theorema egregium

Die Tatsache, dass es keine verzerrungsfreie Karte gibt, war empirisch den Kartografen schon immer bekannt. Gauß gab mit seinem Theoerema egregium den Beweis dazu.

Abb. 23: Carl Friedrich Gauß, 1777 – 1855

Das Theorema egregium von Gauß besagt, dass zwei Flächen, welche eine isometrische, also verzerrungsfreie, Abbildung aufeinander zulassen, dieselbe Flächenkrümmung haben.

Zur Gaußschen Flächenkrümmung kommen wir so: Wir denken uns in einem Flächenpunkt eine zur Fläche senkrechte Stange (Normale) und schneiden die Fläche mit einer Ebene durch diese Normale. Zur Schnittkurve zeichnen wir den dazu passenden Krümmungskreis, der sich am besten an die Schnittkurve anschmiegt. Der Kehrwert des Krümmungskreisradius’ ist die Normalschnittkrümmung. Diese Normalschnittkrümmung variiert, wenn wir die Ebene um die Stange drehen (außer auf einer Kugeloberfläche). Dann nehmen wir das Produkt der maximalen und der minimalen Normalschnittkrümmung. Das ist die Flächenkrümmung. Drei Beispiele:

Da Kugel (Erdkugel) und Ebene (Kartenblatt) unterschiedliche Flächenkrümmungen haben, gibt es keine verzerrungsfreie Karte.

Interessant ist, dass die Zylinderfläche, welche anschaulich als „krumm“ gesehen wird, die Flächenkrümmung null hat. Deshalb kann sie in die Ebene abgewickelt werden. Bei allen so genannten Zylinderkarten, wozu auch die Plattkarte gehört, wird davon Gebrauch gemacht.

5 Flächentreu und winkeltreu

Es gibt also keine verzerrungsfreie Karte. Hingegen gibt es flächentreue Karten, bei denen die Flächenverhältnisse unverzerrt sind, und winkeltreue Karten, bei denen die Winkel unverzerrt sind. Die Plattkarte ist weder flächen- noch winkeltreu.

Flächentreue Karten werden als äquivalent (equivalent), winkeltreue Karten als konform (conformal) bezeichnet.

5.1 Flächentreue Karten

5.1.1 Die flächentreue Karte von Archimedes – Lambert

Die Abbildung 24 zeigt die Karte zusammen mit den Verzerrungsellipsen.

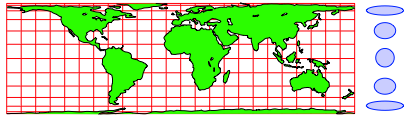
Abb. 24: Flächentreue Karte von Archimedes – Lambert

Das Auseinanderziehen in West-Ost-Richtung in Polnähe wird kompensiert durch ein Zusammenpressen in Süd-Nord-Richtung. Die Verzerrungsellipsen werden gegen die Pole hin immer länger, aber entsprechend immer weniger hoch. Die Fläche bleibt konstant.

Der Abstand zwischen den Breitenkreisen wird gegen die Pole hin verkürzt dargestellt.

Das konstruktive Vorgehen ist in Abbildung 25 dargestellt. Der Kartenträger ist ein Zylinder um den Äquator. Ein Kugelpunkt P wird von der Erdachse aus horizontal auf den Zylinder projiziert. Abwickeln des Zylinders ergibt die Karte.

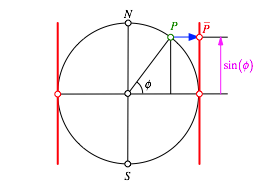
Abb. 25: Konstruktion der flächentreuen Karte

Im Unterschied zur Plattkarte wird jetzt in Süd-Nord-Richtung nicht mehr die geografische Breite abgetragen, sondern nur noch .

5.1.2 Die flächentreue Karte von Mercator – Sanson

Die Idee ist, von der Plattkarte ausgehend die zu großen Maßstäbe in der West-Ost-Richtung durch Einbrutzeln zu kompensieren (Abb. 26). An den Polen wird sogar auf einen Punkte eingebrutzelt.

Die Meridiane werden zu Sinuskurven verbogen. Die äußersten Sinuskurven haben die Amplitude und damit an den Polen eine Steigung zur Vertikalen.

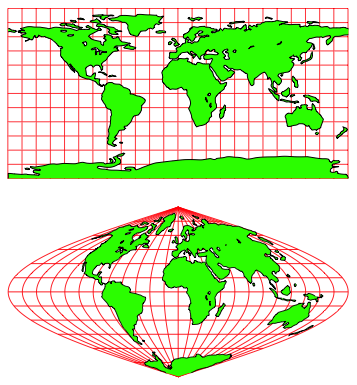
Abb. 26: Einbrutzeln an den Polen. Karte von Mercator – Sanson

5.1.3 Erinnerung an die Schule

Im Unterricht wir der Flächeninhalt eines Kreises bei bekanntem Kreisumfang gemäß Abbildung 27 hergeleitet.

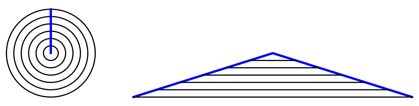
Abb. 27: Kreis und Kreisfläche

Wir denken uns einen Kreis aus 2d-Zwiebelschalen und schneiden von oben her bis in die Mitte ein. Dann fallen die Schalen auseinander und bilden ein flächengleiches gleichschenkliges Dreieck mit der Grundlinie und der Höhe r. Daraus ergibt sich der Flächeninhalt .

Die Schenkel des Dreiecks haben gegenüber der Vertikalen eine Steigung . Wir können also die Mercator – Sanson-Karte (Abb. 26) bündig einpassen (Abb. 28).

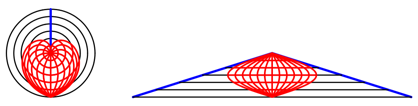
Abb. 28: Einpassen der Mercator – Sanson-Karte

Nun machen wir den Prozess wieder rückwärts und erhalten in der Kreisscheibe eine neue Karte. Diese ist herzförmig und ebenfalls flächentreu (Abb. 29, 30).

5.1.4 Die flächentreue Herzkarte von Stab – Werner

Die Abbildungen 29 und 30 zeigen die flächentreue Karte von Stab – Werner (1514). In der Abbildung 29 erscheinen die Bilder dreier „schräger“ Großkreise.

Abb. 29: Flächentreue Karte von Stab – Werner

Abb. 30: Flächentreue Karte von Stab – Werner

6 Winkeltreue Karten

6.1 Gerhard Mercator

Das Ziel von Mercator war, eine winkeltreue Seekarte für die aufkommende Hochseeschifffahrt herzustellen. Noch heute werden in der Hochseeschifffahrt fast ausschließlich Mercator-Karten (Abb. 32) verwendet. Die Mercator-Karte ist auch Grundlage fast aller offiziellen Karten ist.

Abb. 31: Gerhard Mercator, 1512 – 1594

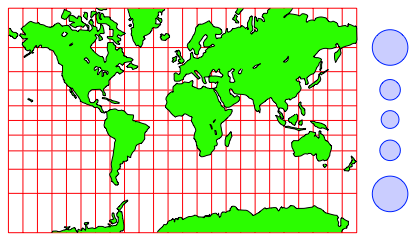
Abb. 32: Winkeltreue Mercator-Karte

Im Unterschied zur flächentreuen Karte (Abb. 24) sind die Abstände zwischen den Bildern der Breitenkreise gegen die Pole zu nicht verdichtet sondern gespreizt und zwar so sehr dass sich die Pole im Unendlichen befinden. Die reale Karte ist also oben und unten abgeschnitten, was bei der Darstellung von Grönland sofort auffällt.

Es wird so stark gespreizt, dass die Maßstäbe in Süd-Nord-Richtung jeweils gleich groß werden wie in West-Ost-Richtung. Wir haben also lokal isometrische Abbildungen. Daher die Winkeltreue. Die Verzerrungsellipsen sind Kreise, die aber gegen die Pole zu immer größer werden. Wir haben global keinen gemeinsamen Maßstab.

6.2 Loxodromen

Wie fahren wir, wenn wir in einem Schiff mit konstantem Kurs fahren (Autopilot mit Kreiselkompass)? Der Winkel zu den Meridianen ist also immer derselbe. In einer Mercator-Karte erscheint diese Kurve daher als Gerade. Solche Kurven heißen Loxodromen („Schräglaufende“). Die Abbildung 33 zeigt eine Loxodrome für einen Kurs von 80°.

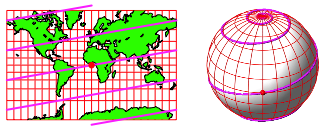
Abb. 33: Loxodrome. Kurs 80°

Die Loxodromen winden sich spiralförmig um die Pole. In der Umgebung der Pole sind es approximativ logarithmische Spiralen. Bei einer stereografischen Projektion (Zentralprojektion) von einem der beiden Pole auf die Tangentialebene im anderen Pol ergibt sich exakt eine logarithmische Spirale. Über Spiralen siehe [Heitzer 1998].

Loxodromen sind keine Großkreise und daher auch nicht kürzeste Verbindungen. Für Kurse in der Nähe von ±90° weichen sie aber nicht stark von den Großkreisbögen ab. Aus praktischen Gründen werden daher in See- und Luftfahrt Loxodromen verwendet.

6.3 Die schöne Kugel

Wir überlagern nun die Mercator-Karte mit einem Quadratraster, der oben und unten ins Unendliche reicht (Abb. 34) und rückübertragen den Raster auf die Kugel.

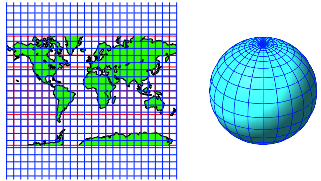
Abb. 34: Quadratraster auf Kugel

Damit erhalten wir einen „Quadratraster“ auf der Kugel.

Eine Loxodrome mit dem Kurs von 45° kann fährt nun den Diagonalen der Quadrate nach (Abb. 35).

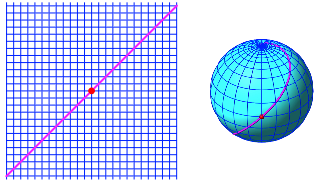
Abb. 35: Diagonalen

Anhang