Hans Walser

Puzzle

SLA-Tagung

15. November 2014, Bern

Zusammenfassung

Es kommen verschiedene Aspekte der Zerlegungsgleichheit zur Sprache: Varianten zu Pythagoras, Gegensatz von Methode und Kreativität, Fragen der Beweiskraft, Symmetrie, Optimierung, rationale und irrationale Rechtecke, Farben und Ästhetik.

1 Der Klassiker

Die Abbildung 1 zeigt einen klassischen Zerlegungsbeweis des Satzes von Pythagoras.

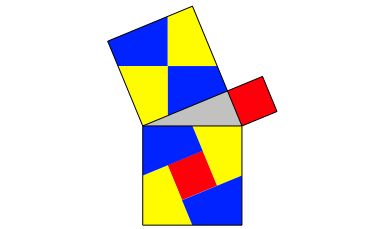
Abb. 1: Klassischer Zerlegungsbeweis zu Pythagoras

2 Aufsetzen von Dreiecken und Vielecken

Nun gilt der Satz von Pythagoras aber auch, wenn wir zum Beispiel regelmäßige Dreiecke an den Seiten des rechtwinkligen Dreiecks ansetzen (Abb. 2).

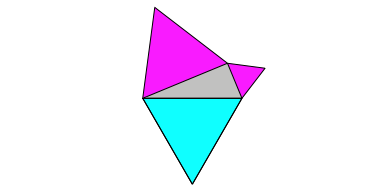
Abb. 2: Zyan = Magenta

Die Abbildung 3 zeigt eine passende Zerlegung.

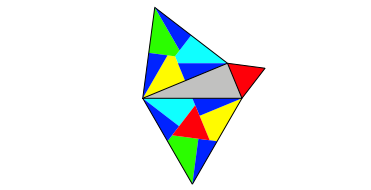
Abb. 3: Zerlegung

Statt Dreiecke können wir beliebige regelmäßige Vielecke ansetzen (Abb. 4 bis 8).

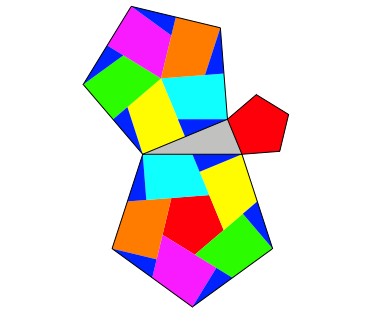
Abb. 4: Fünfecke

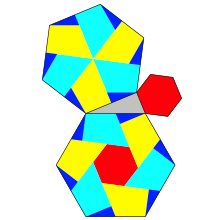
Abb. 5: Sechsecke

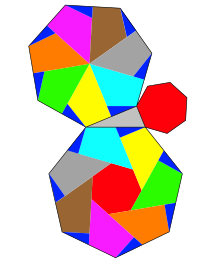
Abb. 6: Siebenecke

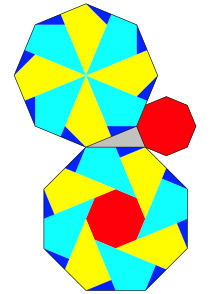
Abb. 7: Achtecke

Wir erkennen ein einheitliches Muster. Natürlich können wir auch Quadrate nach diesem Muster ansetzen (Abb. 8).

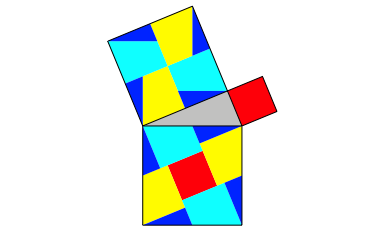
Abb. 8: Quadrate

Die Figur hat einige Verwandtschaft mit dem Klassiker der Abbildung 1.

3 Pythagoreische Dreiecke

Pythagoreische Dreiecke sind besonders einfach. Wir illustrieren das am Beispiel des so genannten „Lehrerdreiecks“ mit dem Seitenverhältnis 3:4:5.

Zunächst können wir die angesetzten regelmäßigen Dreiecke durch kongruente kleine regelmäßige Dreiecke ausschöpfen (Abb. 9). Dabei wird man wohl versuchen, eine kombinatorisch „schöne“ Färbung zu erreichen.

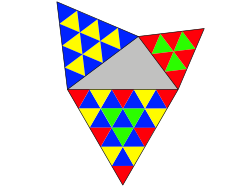
Abb. 9: Das Lehrerdreieck

Wir können die kleinen Dreiecke zu größeren Figuren zusammenfassen (Abb. 10).

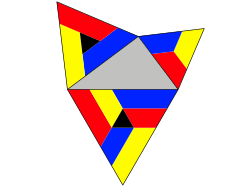
Abb. 10: Größere Puzzle-Teile

Wird auf Symmetrie verzichtet, kann die Anzahl der Teile noch mehr eingeschränkt werden (Abb. 11).

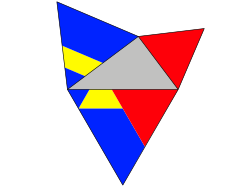
Abb. 11: Asymmetrische Lösung

4 Quadrat und Dreieck

Ein Quadrat und ein flächengleiches Dreieck sind zerlegungsgleich. Die Abbildung 12 zeigt eine klassische Zerlegung (Dudeney, 1903).

Abb. 12: Quadrat und Dreieck

Das Beispiel lässt sich als Gelenkmodell darstellen (Abb. 13).

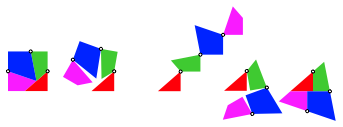
Abb. 13: Gelenkmodell

Die Abbildung 14 zeigt eine weniger elegante Lösung, dafür ist die Basislinie des Dreieckes parallel zu der des Quadrates.

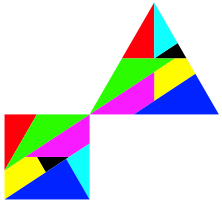
Abb.14: Quadrat und Dreieck

Die Teile in der höhenmäßig oberen Hälfte des Dreieckes müssen beim Einpassen in das Quadrat um 180° gedreht werden (Punktspiegelung). Die übrigen Teile können parallel verschoben werden.

Im Beispiel der Abbildung 15 muss nur das rote Dreieck auf die Spitze gestellt werden.

Abb. 15: Das rote Teil muss umgedreht werden

Im Beispiel der Abbildung 16 müssen die Teile in der rechten Hälfte des Dreieckes vor dem Einpassen ins Quadrat umgewendet werden.

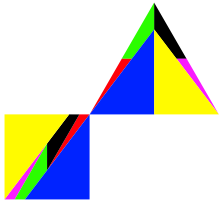
Abb. 16: Umwenden erforderlich

5 Zerlegungsgleichheit und Flächengleichheit

Zerlegungsgleiche Figuren sind trivialerweise flächengleich. Man kann umgekehrt zeigen, dass flächengleiche Polygone auch zerlegungsgleich sind (Satz von W. Wallace - F. W. Bolyai (1832) – P. Gerwien (1833)). Insbesondere sind ein Quadrat und ein flächengleiches gleichseitiges Dreieck zerlegungsgleich (Abb. 12 bis 16).

Eine analoge Aussage gilt im Raum nicht. Zwar sind zerlegungsgleiche Polyeder natürlich volumengleich, aber umgekehrt sind volumengleiche Polyeder nicht immer zerlegungsgleich. Insbesondere sind ein Würfel und ein volumengleiches regelmäßiges Tetraeder (Abb. 17) nicht zerlegungsgleich.

Abb. 17: Würfel und Tetraeder

Die Frage der Zerlegungsgleichheit von Tetraedern wurde von Hilbert als drittes Problem gestellt und von M. W. Dehn (1902) beantwortet. B. F. Kagan (1903) vereinfachte den Beweis. H. Hadwiger (1954) gab eine Verallgemeinerung auf höhere Dimensionen.

Abb. 18: Hugo Hadwiger (1908-1981)

Weitere Bearbeitungen gehen auf D. Benko (2007) und W. Ch. Wittmann (2012) zurück.

6 Zerlegungsgleiche Dreiecke und Polygone

Das Grundverfahren bei Flächenumformungen besteht darin, Dreiecke mit gleicher Höhe und gleicher Grundlinie zu bearbeiten. Die Abbildung 19 zeigt, wie das mit Zerlegungen bewerkstelligt werden kann.

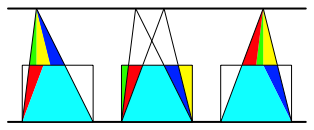
Abb. 19: Zerlegungsgleiche Dreiecke

Sind mehrere Schritte dieser Art erforderlich, ist die bisherige Unterteilung jeweils weiter zu unterteilen. Dies führt bald einmal zu einer großen Anzahl von Puzzle-Teilen. Die Abbildung 20 zeigt eine Illustration des Kathetensatzes. Dabei wurde darauf geachtet, dass die beiden Kathetenquadrate wie auch die beiden Hypotenusenrechtecke jeweils punktsymmetrisch zerschnitten werden.

Abb. 20: Kathetensatz

Es ist mir nicht gelungen, bei der Färbung mich auf vier Farben zu beschränken. Die Schwierigkeit besteht darin, dass jedes Puzzleteil an zwei Orten vorkommt. Man muss also sozusagen auf zwei Hochzeiten gleichzeitig tanzen.

7 Anzahl Farben

Die Abbildung 21 gibt ein einfaches Beispiel, bei welchem zwingend fünf Farben benötigt werden.

Abb. 21: Fünf Farben

Für die Figur links würden gemäß dem Vierfarbensatz vier Farben reichen, man könnte das hellblaue Rechteck ebenfalls gelb färben. Das ist aber nicht kompatibel mit der Figur rechts, weil wir dann zwei gelbe Teile mit gemeinsamer Kante hätten. Umgekehrt könnt man in der Figur rechts das grüne (oder das rote) Rechteck gelb färben, was aber mit der Figur links nicht kompatibel ist.

8 Technisches

Für das Zeichnen habe ich gute Erfahrungen gemacht mit einer Grafiksoftware, welche über einen Vertex-snapper verfügt. Das heißt, man kann Puzzleteile verschieben, bis ein Eckpunkt an einem Eckpunkt eines anderen Puzzleteils einrastet.

9 Optimierung

Zu flächengleichen Polygonen gibt es verschiedene gemeinsame Zerlegungen. Das folgende Beispiel soll Vor- und Nachteile verschiedener gemeinsamer Zerlegungen illustrieren.

Wir bearbeiten ein regelmäßiges Dreieck und ein dazu flächengleiches regelmäßiges Sechseck.

Diese Figuren können zunächst wie folgt gefunden werden. Wir gehen von einer regelmäßigen Kreisteilung in zwölf Teile aus und ergänzen zu Dreieck und Sechseck gemäß Abbildung 22.

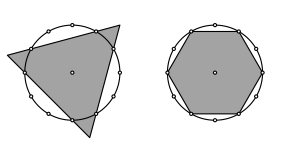
Abb. 22: Dreieck und Sechseck

Wenn wir vom Einheitskreis ausgehen, hat das Dreieck einen Inkreisradius (Abb. 23) und damit eine Seitenlänge . Für den Flächeninhalt ergibt sich .

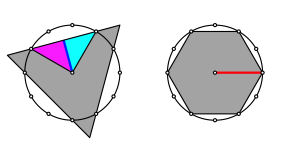
Abb. 23: Flächenberechnung

Das Sechseck hat den Umkreisradius 1 und damit ebenfalls den Flächeninhalt .

Die Abbildung 24 zeigt nun eine gemeinsame Zerlegung.

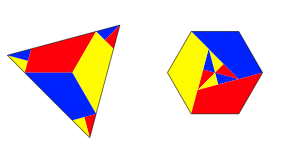
Abb. 24: Gemeinsame Zerlegung

Unter der Website Zerlegungsgleichheit finden wir eine andere Zerlegung (Abb. 25). Dies ist die beste bis anhin bekannte Zerlegung.

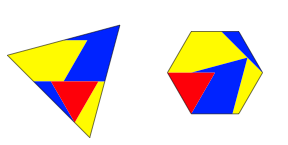
Abb. 25: Zweite Zerlegung

Nachfolgend eine Gegenüberstellung der beiden Zerlegungen.

Zerlegung	Abbildung 24	Abbildung 25
Anzahl Teile total	9	5
Anzahl Formen	2 bzw. 3 je nachdem, ob spiegelbildliche Formen separat gezählt werden	5
Anzahl Farben	3	3
Symmetrie	Zyklische Symmetrie	Keine Symmetrie

Die Zerlegung der Abbildung 24 benötigt insgesamt mehr Puzzleteile, kommt aber mit weniger Puzzleformen aus. Zudem haben die Zerlegungen sowohl des Dreieckes wie des Sechseckes eine zyklische Symmetrie.

10 Zuverlässigkeit von Zerlegungsbeweisen

Die vier in einem Quadratraster gegebenen Puzzleteile der Abbildung 26 können wir scheinbar sowohl zu einem Quadrat wie auch zu einem Rechteck zusammensetzen (Abb. 27).

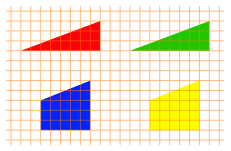
Abb. 26: Puzzleteile

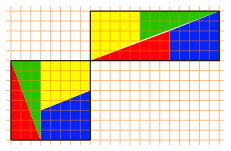
Abb. 27: Quadrat und Rechteck

Nun hat aber das Quadrat die Seitenlänge 8, also den Flächeninhalt 46, das Rechteck die Länge 13 und die Höhe 5 und damit den Flächeninhalt 65. Tatsächlich sehen wir, dass beim Rechteck die Sache nicht ganz aufgeht. Wir haben längs einer Diagonalen einen feinen Zwischenraum. Dies ist ein Parallelogramm mit dem Flächeninhalt 1.

Die Seitenlängen 8 beziehungsweise 13 und 5 sind drei aufeinanderfolgende Fibonacci-Zahlen. Die Abbildung 28 zeigt ein analoges Beispiel mit den drei Fibonacci-Zahlen 13, 21 und 8.

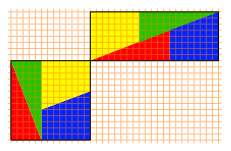
Abb. 28: Quadrat und Rechteck

In diesem Beispiel hat das Quadrat den Flächeninhalt 13² = 169, das Rechteck den Flächeninhalt 21´8 = 168. Im Rechteck haben wir längs der Diagonalen eine Überlappung welche aber von Auge nicht mehr wahrgenommen werden kann.

Allgemein gilt bei drei aufeinander folgenden Fibonacci-Zahlen die schon Kepler bekannte Relation:

Wir dividieren durch den Term links und erhalten:

Beim Grenzübergang n ® ¥ verschwindet der Fehlerterm und wir erhalten:

Dabei ist der Goldene Schnitt (Walser 2013).

Geometrisch haben wir die Situation der Abbildung 29. Diese Figur findet sich im Prinzip bereits bei Euklid Elemente, zweites Buch, §11. Es wird dort auch eine Konstruktion des Goldenen Schnittes angegeben. Der Goldene Schnitt (bei Euklid Stetige Teilung genannt) folgt aber explizit erst im sechsten Buch.

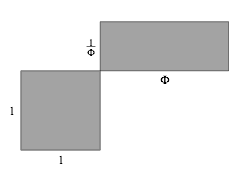
Abb. 29: Quadrat und Rechteck

Die Figur findet sich auch in einem Bild von Jo Niemeyer (Abb. 30).

Abb. 30: Jo Niemeyer. 531 ohne Titel. Acryl auf Leinwand auf Holz. 2014

Für die Ausmaße im Goldenen Schnitt gibt es nun eine saubere gemeinsame Zerlegung (Abb. 31).

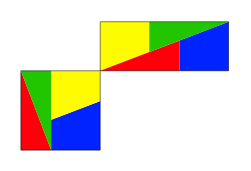
Abb. 31: Zerlegungsgleichheit

Die beteiligen Dreiecke müssen bei dieser Zerlegung um 90° gedreht werden.

11 Rational und irrational

Wir versuchen nun, in der Situation der Abbildung 29 eine Zerlegung mit größtmöglichen Rechtecken zu finden.

Zunächst können wir je ein so genanntes Goldenes Rechteck entfernen (Abb. 32).

Abb. 32: Gemeinsames Goldenes Rechteck

Die grauen Restfiguren sind interessant: Wir haben nun rechts oben ein Restquadrat und links unten ein Restrechteck, das zum ursprünglichen Rechteck rechts oben ähnlich ist.

Nach dem nächsten Schritt (Abb. 33) wiederholt sich in den Restfiguren sogar positionsmäßig die ursprüngliche Situation.

Abb. 33: Rest entspricht der ursprünglichen Situation

Das heißt aber, dass wir unendlich viele Schritte für unsere gemeinsame Zerlegung benötigen. Dies ist letztlich eine Folge der Irrationalität des Goldenen Schnittes. Demgegenüber zeigt die Abbildung 34 ein Beispiel mit einem rationalen Seitenverhältnis.

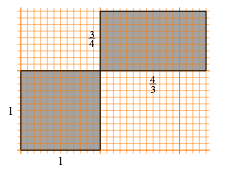
Abb. 34: Rationale Seitenverhältnisse

Schon nach dem ersten Schritt des Abtrennens des größtmöglichen gemeinsamen Rechteckes wiederholt sich die Situation nicht mehr (Abb. 35).

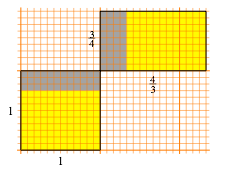
Abb. 35: Erster Abbauschritt

Tatsächlich kommen wir in endlich vielen Schritten zu einer gemeinsamen Rechteckzerlegung (Abb. 36).

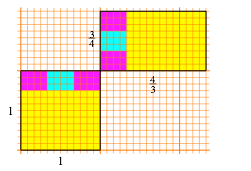
Abb. 36: Zerlegung in Rechtecke

12 Auf der schiefen Bahn

Es gibt eine weitere Art, in der Situation der Abbildung 29 eine gemeinsame Zerlegung zu finden. Als Vorbereitung benötigen wir die parallelen schrägen Linien der Abbildung 37. Die Parallelität lässt sich mit Strahlensätzen nachweisen.

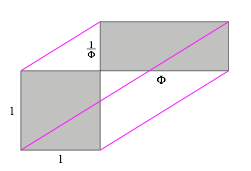
Abb. 37: Die schiefe Bahn

Die Abbildung 38 zeigt nun die ersten Schritte der gemeinsamen Zerlegung. Die blauen Dreiecke sind je die Hälften des misslungenen Versuches der Abbildung 32.

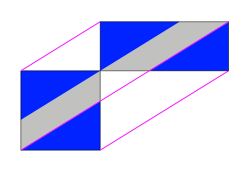
Abb. 38: Erste Schritte

Mit einer geeigneten waagerechten oder senkrechten Halbierung der Restparallelogramme finden wir nun die gemeinsame Zerlegung (Abb. 39).

Abb. 39: Gemeinsame Zerlegung

Dieses Verfahren lässt sich auf flächengleiche Parallelogramme mit gleichen Winkeln verallgemeinern (Abb. 40).

Abb. 40: Verallgemeinerung

13 Farben und Ästhetik

In den Beispielen wurden meistens „reine“ RGB-Farben verwendet. Dadurch werden die Abbildungen etwas gar bunt.

Im Titelbild, das geometrisch der Abbildung 39 entspricht, wurden die Farben etwas „entschärft“.

Dank

Ich danke Jo Niemeyer, Funchal/Portugal, für die Foto der Abbildung 30 sowie weitere Ratschläge in der Farbgebung.

Literatur

Aigner, M., Ziegler, G. (2009): Das Buch der Beweise. Springer, Berlin.

Benko, D. (2007): A New Approach to Hilbert’s Third Problem. Amer. Math. Monthly 114 (2007), 665-676.

Boltianskii, V. G. (1978): Hilbert’s Third Problem. V. H. Winston & Sons, Washington D.C.

Dehn, M. (1900): Über raumgleiche Polyeder. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II, 345-354.

Dehn, M. (1902): Über den Rauminhalt. Math. Annalen 55, 465-478.

Frederickson, Greg N. (1997): Dissections: plane & fancy. Cambridge University Press.

Frederickson, Greg N. (2002): Hinged Dissections. Swinging & Twisting. Cambridge University Press. ISBN 0-521-81192-9. http://www.cs.purdue.edu/homes/gnf/book2.html

Hadwiger, Hugo (1949/50): Zum Problem der Zerlegungsgleichheit der Polyeder. Archiv der Math. 2, 441-444.

Hadwiger, Hugo (1954): Zum Problem der Zerlegungsgleichheit k-dimensionaler Polyeder. Math. Annalen, Bd. 127, 170-174.

Kagan, B. (1903): Über die Transformation der Polyeder. Math. Annalen 57, 421-424.

Lindgren, Harry (1972): Geometric Dissections. Revised and enlarged by Greg Frederickson. New York: Dover.

Walser, Hans (6. Auflage) (2013). Der Goldene Schnitt. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Wittmann, Erich CH. (2012): Elementarisierung von Benkos Lösung des 3. Hilbertschen Problems. Elem. Math. 67, 45-50.

Websites

Hinged Dissections (Abgerufen 17. 8. 2014)
http://www.cs.purdue.edu/homes/gnf/book2.html

Puzzles (Abgerufen 17. 8. 2014)
http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Puzzles/index.html

Zerlegungsgleichheit (Abgerufen 17. 8. 2014)
http://mathworld.wolfram.com/Dissection.html

Version 16. Oktober 2014, 07:27 Uhr