Hans Walser

 

 

Vom Strahlensatz zum Strahlensatz

Motive und PhŠnomene

 

GDM Jahresversammlung 2015

Basel

9. – 13. Februar 2015

 

Zusammenfassung

Ausgehend von einem didaktischen Fehler ergibt sich eine Gedankenreise, welche beim Strahlensatz beginnt und Ÿber verschiedene Stationen wie Parabel, projektive Geometrie, Symmetrie, Faltgeometrie und rechte Winkel wieder zum Strahlensatz fŸhrt.

 

1        Faltgeometrie

Auf der RŸckseite eines Blattes (Querformat) tragen wir am unteren Rand zwei mal drei Marken ein (Abb. 1a). Dann wenden wir das Blatt und wŠhlen einen Punkt (Abb. 1b).

 

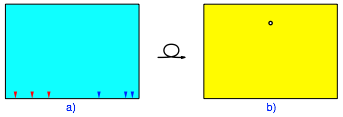
Abb. 1: Zwei mal drei Marken. Punkt wŠhlen

 

Nun falten wir die erste Markierung auf den Punkt ein und wieder zurŸck (Abb. 2).

 

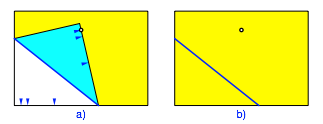
Abb. 2: Erster Faltschritt

 

Nun falten wir die zweite Markierung auf den Punkt ein und wieder zurŸck (Abb. 3).

 

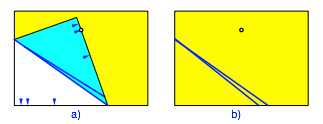
Abb. 3: Zweiter Faltschritt

 

Schlie§lich erhalten wir zwei Scharen von je drei Faltlinien (Abb. 4a). Die wechselseitigen Schnittpunkte teilen jeweils auf jeder Schar im gleichen VerhŠltnis (Abb. 4b). Das ist auch das VerhŠltnis der ursprŸnglich gewŠhlten Marken (Abb. 1a).

 

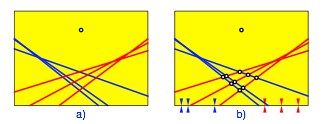
Abb. 4: Faltlinien. TeilverhŠltnisse

 

Diese Situation erinnert an den Strahlensatz.

2        Strahlensatz

In der Strahlensatzfigur (Abb. 5) haben wir aber einerseits eine Schar von parallelen Geraden und andererseits eine Schar von Geraden durch einen Punkt. Das sind begrifflich asymmetrische Vorgaben. Die Satzaussage ist aber symmetrisch: in beiden Geradenscharen sind je entsprechende TeilverhŠltnisse gleich.

 

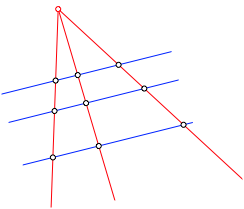
Abb. 5: Strahlensatzfigur

 

Die Faltfigur der Abbildung 4b ist begrifflich symmetrisch. Ebenso erhalten wir eine begrifflich symmetrische Figur mit Winkeleisen (Abb. 6). Dazu verfahren wir wie folgt.

3        Winkeleisen

 

         

Abb. 6: Winkeleisen: Anschlagwinkel und Spenglerwinkel

 

Wir beginnen mit einem Punkte F und einer nicht durch F verlaufenden Geraden t. Nun passen wir gemŠ§ Abbildung 7 zwei Sets von je drei rechten Winkeln (rote und blaue ãWinkeleisenÒ) ein so, dass die Scheitel der rechten Winkel auf t liegen und jeweils ein Schenkel durch F verlŠuft. Die anderen Schenkel schneiden sich wechselseitig.

 

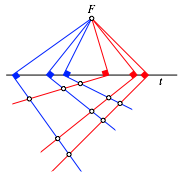
Abb. 7: Winkeleisen

 

Diese Schnittpunkte unterteilen die roten Schenkel im gleichen VerhŠltnis. Im Beispiel der Abbildung 7 ist es das VerhŠltnis 2:1. Ebenso unterteilen sie die blauen Schenkel im gleichen VerhŠltnis. Im Beispiel der Abbildung 7 ist es das VerhŠltnis 5:2.

Wir sind geneigt in unserem Anschauungsraum die Figur rŠumlich zu interpretieren. Dann allerdings haben wir das GefŸhl, dass die auf uns zukommende Ebene nach unten hŠngt. Das hŠngt damit zusammen, dass die Figur keine perspektivische Darstellung ist.

4        Beweis

Wir legen ein Koordinatensystem gemŠ§ der Abbildung 8 zugrunde. Als x-Achse wŠhlen wir die Gerade t. Der Punkt F habe die Koordinaten F(0, 1). Wir wŠhlen exemplarisch einen roten Winkel mit dem Scheitelpunkt (a, 0) und einen blauen Winkel mit dem Scheitelpunkt (b, 0).

 

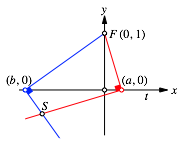
Abb. 8: Koordinaten

 

Der zweite rote Schenkel hat die Gleichung , der zweite blaue Schenkel die Gleichung . FŸr den Schnittpunkt S der beiden Schenkel ergeben sich die Koordinaten . Summe und Produkt, die beiden einfachen Gottesgaben.

Die drei roten Winkel und die drei blauen Winkel der Abbildung 1 nummerieren wir mit  beziehungsweise . Die Scheitel dieser Winkel seien bei  beziehungsweise .

Der Punkt  als Schnittpunkt des i-ten roten Schenkels mit dem j-ten blauen Schenkel hat die Koordinaten .

Nun berechnen wir das TeilverhŠltnis auf dem i-ten roten Schenkel:

FŸr die Strecke  erhalten wir:

 

 

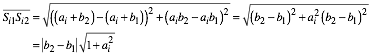
Analog ergibt sich fŸr die Strecke :

 

Bei der VerhŠltnisbildung kŸrzt sich der Wurzelfaktor heraus:

 

Wir sehen, dass das TeilverhŠltnis unabhŠngig vom Index i ist, das hei§t, es ist auf allen roten Schenkeln gleich. Es ist zudem gleich dem TeilverhŠltnis der Scheitel der drei blauen Winkel.

Aus SymmetriegrŸnden gilt das Analoge fŸr die TeilverhŠltnisse auf den blauen Schenkeln.

Im Abschnitt 14.1 eine Beweisvariante, die mit Sehnenvierecken arbeitet.

5        Link zum Strahlensatz

Wir modifizieren die Figur der Abbildung 7, indem wir mit dem Punkt F gegen die Gerade t streben.

Die beiden Winkelscharen behandeln wir aber ungleich, um die fŸr den Strahlensatz nštige Asymmetrie zu erreichen. Bei den blauen Winkeln lassen wir die Scheitelpunkte auf t fest. Diese Winkel werden also gedreht. Bei den roten Winkeln lassen wir die Richtungen fest. Diese Winkel werden parallel verschoben.

Da die TeilverhŠltnisse bei den Winkelscheiteln sich nicht verŠndern, bleiben auch die TeilverhŠltnisse auf den Schenkeln invariant.

Die Abbildung 9 illustriert diesen Modifikationsprozess in mehreren Schritten. Im Grenzfall mit F auf t stehen die blauen Schenkel senkrecht auf t, sind also untereinander parallel. Die roten Schenkel verlaufen durch F. Wir haben den gewšhnlichen Strahlensatz.

 

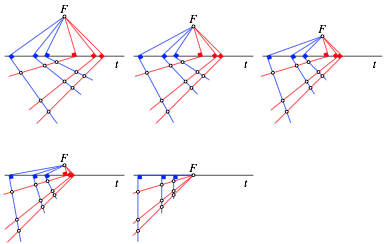
Abb. 9: Modifikation

 

6        Motivation

Auf einem Arbeitsblatt (8. Schuljahr) ist zu lesen:

 

Eigenschaften der Trapeze

¥         Jedes Trapez hat ein Paar gegenŸberliegender paralleler Seiten.

¥         Beide Mittellinien halbieren sich.

 

Da wurde moniert, das sei zwar fachlich richtig, aber didaktisch falsch. Die erste Zeile sei definierend fŸr die Trapeze, die zweite Zeile gelte aber fŸr jedes Viereck (Abb. 10a). Vielleicht sollte hier speziell auf die Mittellinien hingewiesen werden, weil eine davon nachher fŸr die FlŠchenformel gebraucht wird.

 

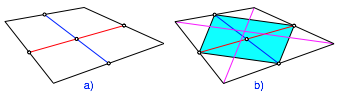
Abb. 10: Mittellinien halbieren sich

 

Die Halbierungseigenschaft kann Ÿber das diagonalenparallele Parallelogramm nachgewiesen werden, welches durch die Seitenmitten des allgemeinen Viereckes aufgespannt wird (Abb. 10b).

Dieser didaktische ãFehlerÒ erwies sich als sehr anregend: was ist, wenn Mitte und halbieren durch Drittel und dritteln ersetzt wird?

7        Dritteln

Dritteln sich Drittellinien gegenseitig?

Der Sonderfall des Trapezes erweist sich als einfach, da wir den Strahlensatz anwenden kšnnen (Abb. 11a).

 

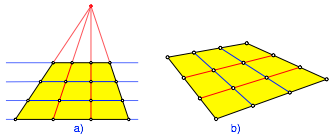
Abb. 11: Sonderfall Trapez. Allgemeines Viereck

 

Wir vermuten aufgrund der Zeichnung (Abb. 11b), dass sich auch im allgemeinen Fall die Drittellinien gegenseitig dritteln. Wie ist es mit anderen TeilverhŠltnissen?

Im Abschnitt 14.2 ein elementarer Beweis fŸr die Drittelung im allgemeinen Viereck.

Die Abbildung 12 zeigt die Situation bei Viertelung und Achtelung. Wir kšnnen Parallelogramme einpassen.

 

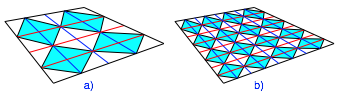
Abb. 12: Viertel-Linien und Achtel-Linien

 

Die Parallelogramme liegen allerdings nicht schšn in einer Flucht.

8        Zwischenspiel: Perspektive

Die Abbildung 13 zeigt das projektive Bild eines Schachbrettes, ein so genanntes Moebiusnetz.

 

Abb. 13: Schachbrett und Weg des LŠufers

 

Im Unterschied zur Abbildung 12 sind die blauen Vierecke keine Parallelogramme. DafŸr sind sie ãstimmigÒ.

9        Beweis fŸr den allgemeinen Fall

Wir teilen zwei gegenŸberliegende Seiten des Vierecks im VerhŠltnis λ, die beiden anderen Seiten im VerhŠltnis μ. Wir verbinden dann die Teilpunkte gegenŸberliegender Seiten. Zu zeigen ist: diese Verbindungslinien teilen sich gegenseitig in den VerhŠltnissen λ und μ. Wir verwenden die Bezeichnungen der Abbildung 14.

 

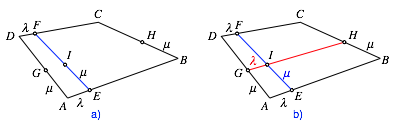
Abb. 14: Beweisidee

 

ZunŠchst teilen wir die Seiten AB und DC im gleichen VerhŠltnis λ. Es ist also:

 

In der Abbildung 14 ist λ = 0.2.

Dann teilen wir die Strecken AD, BC und EF im gleichen VerhŠltnis μ:

 

In der Abbildung 14 ist μ = 0.45.

Zu zeigen ist: Die Punkte G, I und H sind kollinear, also

 

Das ist eine Vektorerei. Es ist:

 

 

Weiter ist:

 

 

Und weiter:

 

 

Somit ist:

 

Somit sind die Punkte G, I und H kollinear.

10    Viereckraster

FŸr ganze Zahlen λ und μ erhalten wir ein Viereckraster wie folgt. Wir verlŠngern die Viereckseiten und tragen Vielfache der SeitenlŠngen ab (Abb. 15a).

 

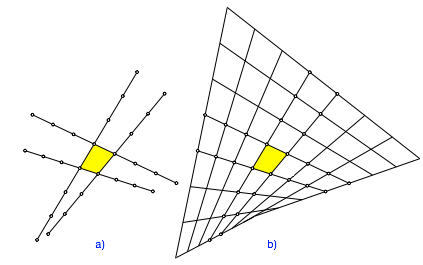
Abb. 15: Erster Schritt. ErgŠnzung zum Viereckraster

 

Anschlie§end ergŠnzen wir zum Viereckraster (Abb. 15b). Jede Rasterlinie der einen Schar wird von den Rasterlinien der anderen Schar in gleichmŠ§igen AbstŠnden geschnitten.

Wir sehen, dass sich beim †berschneiden der Linien was Spannendes anbahnt.

11    Parabel

Wenn wir das Viereckraster fortsetzen, Ÿberschneiden sich die Rasterlinien. Als Enveloppe entsteht eine Kurve (Abb. 16). Die Kurve sieht aus wie eine Parabel, es kšnnte aber auch eine Ellipse sein. Was nun?

 

Abb. 16: Parabel

 

12    Sichtumkehr: Beginn mit Parabel

Wir zeichnen zweimal drei Tangenten an eine Parabel und bestimmen exemplarisch die TeilverhŠltnisse zwischen den wechselseitigen Schnittpunkten (Abb. 17).

 

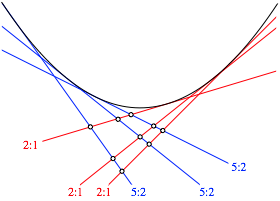
Abb. 17: Tangenten an Parabel

 

Wenn wir dasselbe Spielchen mit einem Kreis machen (Abb. 18a), haben wir zwar wieder Winkeleisen wie in der Abbildung 7, aber keine konstanten TeilverhŠltnisse. Mit einer Ellipse kann es daher auch nicht funktionieren, das sich eine Ellipse mit einer affinen Abbildung unter Erhaltung der TeilverhŠltnisse auf einen Kreis abbilden lŠsst.

 

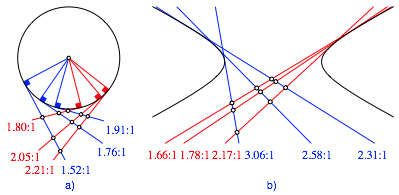
Abb. 18: Mit dem Kreis und Hperbel funktioniert es nicht

 

Auch mit der Hyperbel (Abb. 18b) ist nichts zu wollen.

Die Parabel, der Exot unter den Kegelschnitten, ist also der interessante Fall.

13    Zirkel und Lineal

Die Kegelschnitte kšnnen punktweise mit Zirkel und Lineal konstruiert werden. FŸr die Parabel benštigen wir eine Gerade (Leitlinie) und einen Punkt (Brennpunkt). Die Abbildung 19 illustriert exemplarisch die Konstruktionen von zwei Punkten. Die jeweils gleichfarbigen AbstŠnde sind gleich gro§.

 

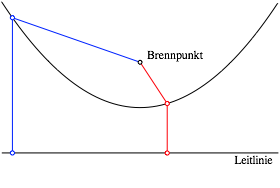
Abb. 19: Konstruktion von Parabelpunkten

 

Die Tangenten ergeben sich als Mittelsenkrechte (Abb. 20).

 

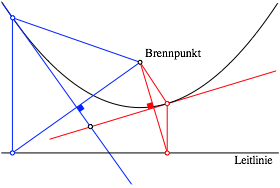
Abb. 20: Tangenten als Mittelsenkrechte

 

In unserem Beispiel aus der Faltgeometrie (Abb. 4) spielen der Punkt die Rolle des Brennpunktes und die untere Papierkante die Rolle der Leitlinie.

Die rechten Winkel in der Abbildung 20 liegen auf der Scheiteltangente der Parabel (Abb. 21). Dabei erkennen wir auch wieder die Winkeleisen der Abbildung 7.

 

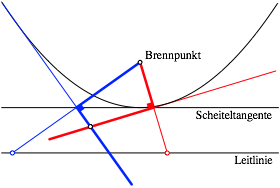
Abb. 21: Scheiteltangente und Winkeleisen

 

Damit schlie§t sich der Gedankenkreis.

14    ErgŠnzungen und Variationen

Im Folgenden einige ErgŠnzungen, die mir von Kolleginnen und Kollegen zugekommen sind.

14.1  Sehnenvierecke

Der im Abschnitt 4 vorgestellte Beweis lŠsst sich auch mit Sehnenvierecken durchfŸhren. Die Idee dazu verdanke ich Emese Vargyas, Mainz.

Die Abbildung 22 entspricht der Abbildung 8; das Koordinatensystem ist weggelassen. Wegen der rechten Winkel bei A und B ist das Viereck SAFB ein Sehnenviereck (Abb. 22a). In der Abbildung 22b ist zusŠtzlich das Sehnenviereck CAFB eingezeichnet.

In diesem Viereck gilt . Dabei ist s auch der Abstand von S von der Geraden

AB.

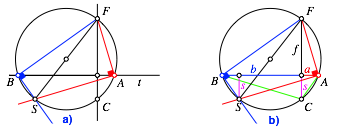
Abb. 22: Sehnenviereck

 

In der Abbildung 23 sind nun drei blaue rechte Winkel eingetragen.

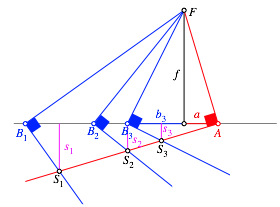
Abb. 23: Drei blaue rechte Winkel

 

Dabei gilt:

 

Somit ist auch:

 

 

Das TeilverhŠltnis auf dem roten Schenkel ist also unabhŠngig von der Position des Punktes A.

FŸr diese †berlegungen benštigen wir die gewšhnlichen StrahlensŠtze.

14.2  Dritteln

Der Nachweis, dass sich Drittellinien gegenseitig dritteln (Abb. 11b) lŠsst sich mit folgender †berlegung von Hans Humenberger, Wien, fŸhren.

 

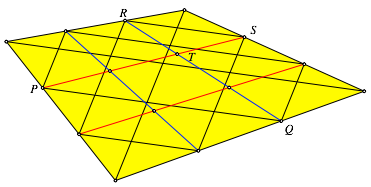
Abb. 24: Drittellinien

 

Die schwarzen Linien in der Abbildung 24 sind parallel zu den Viereckdiagonalen. Auf Grund der gewšhnlichen StrahlensŠtze ist die Strecke PQ doppelt so lang wie die Strecke RS. Daher drittelt der Schnittpunkt T die Strecken PS und QR (ãX-FigurÒ). Analog fŸr die Ÿbrigen Schnittpunkte der roten und blauen Strecken.

 

Last modified: 20. Februar 2015