Hans Walser

 

 

Ein namenloses PhŠnomen

 

Arbeitskreis Geometrie der GDM

SaarbrŸcken

11. – 13. September 2015

 

Zusammenfassung

Ein Faltspiel und ein Spiel mit rechten Winkelhaken fŸhren beide zu einem symmetrischen PhŠnomen, welches im Lehrplan nicht kodifiziert ist. Der (asymmetrische) Strahlensatz erweist sich als Grenzfall.

Die †berlegungen wurden angeregt durch einen didaktischen Fehler in einem Arbeitsblatt fŸr das 8. Schuljahr. 

 

 

1        Eine Warum-Litanei

1.1      Die Litanei

Im Folgenden einige PhŠnomene, die zum Nachdenken anregen:

á           Warum braucht es fŸr die Berechnung der HypotenusenlŠnge den Umweg Ÿber die KathetenflŠchen?

á           Warum ist der Satz des Pythagoras asymmetrisch?

á           Warum ist der Strahlensatz asymmetrisch?

á           Warum fehlt beim 1d-Kreis-Inhalt das ¹?

á           Warum ist das 3d-Analogon zum Quadrat nicht eindeutig?

1.2      Kommentare

Warum braucht es fŸr die Berechnung der HypotenusenlŠnge den Umweg Ÿber die KathetenflŠchen? – Diese Frage wurde mir von einem SchŸler gestellt. Ich kann sie nicht beantworten.

Warum ist der Satz des Pythagoras asymmetrisch? – Wir haben ein Hypotenusenquadrat, aber zwei Kathetenquadrate.

Genau in einem Viereck mit orthogonalen Diagonalen sind die beiden Summen der QuadratflŠchen Ÿber gegenŸberliegenden Seiten gleich gro§ (Abb. 1).

 

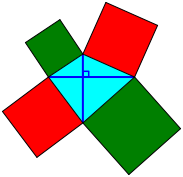
Abb. 1: Rot gleich GrŸn

 

Warum ist der Strahlensatz asymmetrisch? – Diese Frage wird im Folgenden diskutiert aber nicht beantwortet.

Warum fehlt beim 1d-Kreis-Inhalt das ¹? – FŸr den 2d-Kreis haben wir den FlŠcheninhalt , fŸr die 3d-Kugel den Volumeninhalt . Der 1d-ãKreisÒ, also das Intervall, das vom Mittelpunkt aus auf beiden Seiten die LŠnge r aufweist, hat den LŠngeninhalt 2r. Die Kreiszahl ¹ fehlt. Das Problem ãlšstÒ sich bei der Berechnung der Inhalte von Hyperkugeln hšherer Dimensionen. Die Tabelle 1 gibt die Formeln.

 

Dimension

Inhaltsformel

0

-

1

2

3

4

5

6

7

Tab. 1: Inhaltsformeln

 

Allgemein gilt: 

FŸr gerade Dimension n ist der Inhalt . (FŸr die Dimension 0 gilt also der Inhalt .)

FŸr ungerade Dimension n ist der Inhalt .

Bemerkung: Der ParitŠtsunterschied kann mit Hilfe der Gamma-Funktion ŸberbrŸckt werden. Wir erhalten den Inhalt .

Warum ist das 3d-Analogon zum Quadrat nicht eindeutig? – Wenn wir uns an den Quadratseiten orientieren, erhalten wir als rŠumliches Analogon den WŸrfel. Wenn wir uns an den Quadratdiagonalen orientieren, ergibt sich das regulŠre Oktaeder (Abb. 2).

 

Abb. 2: Analoga des Quadrates

 

2        Faltgeometrie

Auf der RŸckseite eines Blattes (Querformat) tragen wir am unteren Rand zwei mal drei Marken ein (Abb. 3a). Dann wenden wir das Blatt und wŠhlen einen Punkt (Abb. 3b).

 

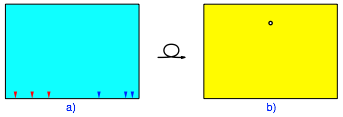
Abb. 3: Zwei mal drei Marken. Punkt wŠhlen

 

Nun falten wir die erste Markierung auf den Punkt ein und wieder zurŸck (Abb. 4).

 

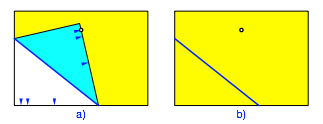
Abb. 4: Erster Faltschritt

 

Nun falten wir die zweite Markierung auf den Punkt ein und wieder zurŸck (Abb. 5).

 

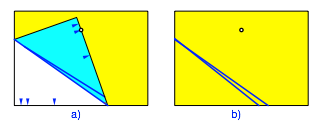
Abb. 5: Zweiter Faltschritt

 

Schlie§lich erhalten wir zwei Scharen von je drei Faltlinien (Abb. 6a). Die wechselseitigen Schnittpunkte teilen jeweils auf jeder Schar im gleichen VerhŠltnis (Abb. 6b). Das ist auch das VerhŠltnis der ursprŸnglich gewŠhlten Marken (Abb. 3a).

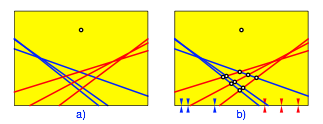
Abb. 6: Faltlinien. TeilverhŠltnisse

 

Diese Situation erinnert an den Strahlensatz.

3        Strahlensatz

In der Strahlensatzfigur (Abb. 7) haben wir aber einerseits eine Schar von parallelen Geraden und andererseits eine Schar von Geraden durch einen Punkt. Das sind begrifflich asymmetrische Vorgaben. Die Satzaussage ist aber symmetrisch: in beiden Geradenscharen sind je entsprechende TeilverhŠltnisse gleich.

 

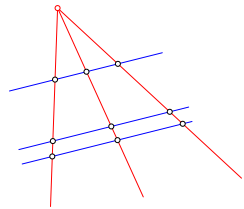
Abb. 7: Strahlensatzfigur

 

Die Faltfigur der Abbildung 6b ist begrifflich symmetrisch. Ebenso erhalten wir eine begrifflich symmetrische Figur mit Winkeleisen (Abb. 8). Dazu verfahren wir wie folgt.

4        Winkeleisen

 

         

Abb. 8: Winkeleisen: Anschlagwinkel und Spenglerwinkel

 

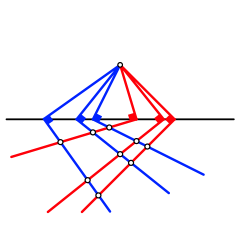
Wir beginnen mit einem Punkt F und einer nicht durch F verlaufenden Geraden t. Nun passen wir gemŠ§ Abbildung 9 zwei Sets von je drei rechten Winkeln (rote und blaue ãWinkeleisenÒ) ein so, dass die Scheitel der rechten Winkel auf t liegen und jeweils ein Schenkel durch F verlŠuft. Die anderen Schenkel schneiden sich wechselseitig.

 

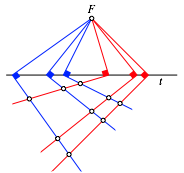
Abb. 9: Winkeleisen

 

Diese Schnittpunkte unterteilen die roten Schenkel im gleichen VerhŠltnis. Im Beispiel der Abbildung 9 ist es das VerhŠltnis 2:1. Ebenso unterteilen sie die blauen Schenkel im gleichen VerhŠltnis. Im Beispiel der Abbildung 9 ist es das VerhŠltnis 5:2.

Wir sind geneigt in unserem Anschauungsraum die Figur rŠumlich zu interpretieren. Dann allerdings haben wir das GefŸhl, dass die auf uns zukommende Ebene nach unten hŠngt. Das hŠngt damit zusammen, dass die Figur keine perspektivische Darstellung ist.

5        Beweis

Wir legen ein Koordinatensystem gemŠ§ der Abbildung 10 zugrunde. Als x-Achse wŠhlen wir die Gerade t. Der Punkt F habe die Koordinaten F(0, 1). Wir wŠhlen exemplarisch einen roten Winkel mit dem Scheitelpunkt (a, 0) und einen blauen Winkel mit dem Scheitelpunkt (b, 0).

 

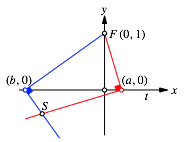
Abb. 10: Koordinaten

 

Der zweite rote Schenkel hat die Gleichung , der zweite blaue Schenkel die Gleichung . FŸr den Schnittpunkt S der beiden Schenkel ergeben sich die Koordinaten . Summe und Produkt, die beiden einfachen Gottesgaben.

Die drei roten Winkel und die drei blauen Winkel der Abbildung 1 nummerieren wir mit  beziehungsweise . Die Scheitel dieser Winkel seien bei  beziehungsweise .

Der Punkt  als Schnittpunkt des i-ten roten Schenkels mit dem j-ten blauen Schenkel hat die Koordinaten .

Nun berechnen wir das TeilverhŠltnis auf dem i-ten roten Schenkel:

FŸr die Strecke  erhalten wir:

 

 

 

Analog ergibt sich fŸr die Strecke :

 

 

Bei der VerhŠltnisbildung kŸrzt sich der Wurzelfaktor heraus:

 

 

Wir sehen, dass das TeilverhŠltnis unabhŠngig vom Index i ist, das hei§t, es ist auf allen roten Schenkeln gleich. Es ist zudem gleich dem TeilverhŠltnis der Scheitel der drei blauen Winkel.

Aus SymmetriegrŸnden gilt das Analoge fŸr die TeilverhŠltnisse auf den blauen Schenkeln.

Im Abschnitt 14 eine Beweisvariante, die mit Sehnenvierecken arbeitet.

6        Link zum Strahlensatz

Wir modifizieren die Figur der Abbildung 9, indem wir mit dem Punkt F gegen die Gerade t streben.

Die beiden Winkelscharen behandeln wir aber ungleich, um die fŸr den Strahlensatz nštige Asymmetrie zu erreichen. Bei den blauen Winkeln lassen wir die Scheitelpunkte auf t fest. Diese Winkel werden also gedreht. Bei den roten Winkeln lassen wir die Richtungen fest. Diese Winkel werden parallel verschoben.

Da die TeilverhŠltnisse bei den Winkelscheiteln sich nicht verŠndern, bleiben auch die TeilverhŠltnisse auf den Schenkeln invariant.

Die Abbildung 11 illustriert diesen Modifikationsprozess in mehreren Schritten. Im Grenzfall mit F auf t stehen die blauen Schenkel senkrecht auf t, sind also untereinander parallel. Die roten Schenkel verlaufen durch F. Wir haben den gewšhnlichen Strahlensatz.

 

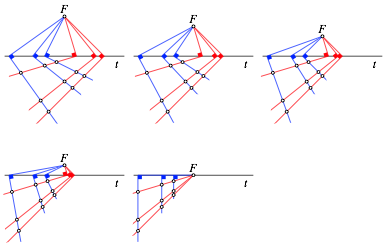
Abb. 11: Modifikation

 

7        Motivation

Auf einem Arbeitsblatt (8. Schuljahr) ist zu lesen:

 

Eigenschaften der Trapeze

¥         Jedes Trapez hat ein Paar gegenŸberliegender paralleler Seiten.

¥         Beide Mittellinien halbieren sich.

 

Da wurde moniert, das sei zwar fachlich richtig, aber didaktisch falsch. Die erste Zeile sei definierend fŸr die Trapeze, die zweite Zeile gelte aber fŸr jedes Viereck (Abb. 12a). Vielleicht sollte hier speziell auf die Mittellinien hingewiesen werden, weil eine davon nachher fŸr die FlŠchenformel gebraucht wird.

 

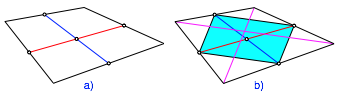
Abb. 12: Mittellinien halbieren sich

 

Die Halbierungseigenschaft kann Ÿber das diagonalenparallele Parallelogramm nachgewiesen werden, welches durch die Seitenmitten des allgemeinen Viereckes aufgespannt wird (Abb. 12b).

Dieser didaktische ãFehlerÒ erwies sich als sehr anregend: was ist, wenn Mitte und halbieren durch Drittel und dritteln ersetzt wird?

8        Dritteln

Dritteln sich Drittellinien gegenseitig?

Der Sonderfall des Trapezes erweist sich als einfach, da wir den Strahlensatz anwenden kšnnen (Abb. 13a).

 

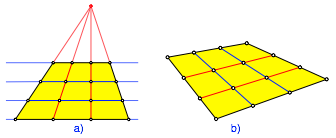
Abb. 13: Sonderfall Trapez. Allgemeines Viereck

Wir vermuten aufgrund der Zeichnung (Abb. 13b), dass sich auch im allgemeinen Fall die Drittellinien gegenseitig dritteln. Dies kann gemŠ§ einer Mitteilung von Hans Humenberger, Wien, wie folgt gezeigt werden (Abb. 14).

 

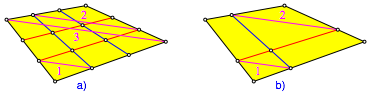
Abb. 14: Beweisfigur

 

Wir fŸhren gemŠ§ Abbildung 14a eine Diagonale und dazu parallele Strecken ein. Diese haben auf Grund des Strahlensatzes die angegebenen LŠngenverhŠltnisse. Die Abbildung 14b zeigt, dass diese zur Drittelung beim angegebenen Punkt fŸhrt. FŸr die anderen Schnittpunkte im Viereck kann analog Ÿberlegt werden.

Nun ist es allerdings so, dass diese Idee nicht auf Viertelung, FŸnftelung, ... Ÿbertragen werden kann.

9        Beweis fŸr den allgemeinen Fall

Wir teilen zwei gegenŸberliegende Seiten des Vierecks im VerhŠltnis λ, die beiden anderen Seiten im VerhŠltnis μ. Wir verbinden dann die Teilpunkte gegenŸberliegender Seiten. Zu zeigen ist: diese Verbindungslinien teilen sich gegenseitig in den VerhŠltnissen λ und μ. Wir verwenden die Bezeichnungen der Abbildung 15.

 

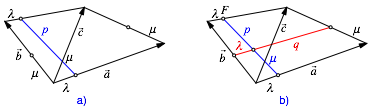
Abb. 15: Beweisidee

 

FŸr die eingezeichnete blaue Strecke p erhalten wir die Parameterdarstellung:

 

 

FŸr die eingezeichnete rote Strecke q erhalten wir die Parameterdarstellung:

 

 

Der Schnittpunkte ergibt sich offensichtlich fŸr  und . Das war zu zeigen.

Bemerkung 1: Der Vektor  misst die Abweichung des Viereckes vom Parallelogramm. Im Parallelogramm ist die TeilverhŠltniseigenschaft trivial.

Bemerkung 2: Die EinschrŠnkungen  und  beziehen sich auf die eingezeichneten Strecken, sind aber fŸr den Beweisgang unerheblich. Sie werden im Folgenden weggelassen.

10    Viereckraster

FŸr ganze Zahlen λ und μ erhalten wir ein Viereckraster wie folgt. Wir verlŠngern die Viereckseiten und tragen Vielfache der SeitenlŠngen ab (Abb. 16a).

 

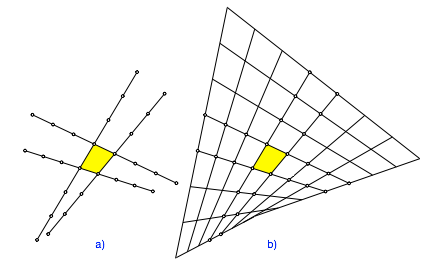
Abb. 16: Erster Schritt. ErgŠnzung zum Viereckraster

 

Anschlie§end ergŠnzen wir zum Viereckraster (Abb. 16b). Jede Rasterlinie der einen Schar wird von den Rasterlinien der anderen Schar in gleichmŠ§igen AbstŠnden geschnitten.

Wir sehen, dass sich beim †berschneiden der Linien was Spannendes anbahnt.

 

11    Parabel

Wenn wir das Viereckraster fortsetzen, Ÿberschneiden sich die Rasterlinien. Als Enveloppe entsteht eine Kurve (Abb. 17). Die Kurve sieht aus wie eine Parabel, es kšnnte aber auch eine Ellipse sein. Was nun?

 

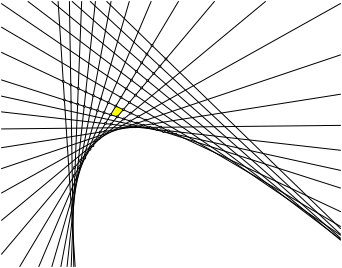
Abb. 17: Parabel

 

12    Sichtumkehr: Beginn mit Parabel

Wir zeichnen zweimal drei Tangenten an eine Parabel und bestimmen exemplarisch die TeilverhŠltnisse zwischen den wechselseitigen Schnittpunkten (Abb. 18).

 

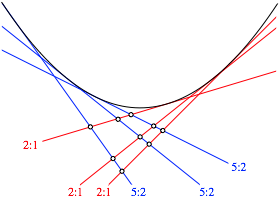
Abb. 18: Tangenten an Parabel

 

Wenn wir dasselbe Spielchen mit einem Kreis machen (Abb. 19a), haben wir zwar wieder Winkeleisen wie in der Abbildung 9, aber keine konstanten TeilverhŠltnisse. Mit einer Ellipse kann es daher auch nicht funktionieren, das sich eine Ellipse mit einer affinen Abbildung unter Erhaltung der TeilverhŠltnisse auf einen Kreis abbilden lŠsst.

 

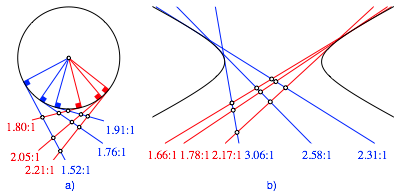
Abb. 19: Mit dem Kreis und der Hyperbel funktioniert es nicht

 

Auch mit der Hyperbel (Abb. 19b) ist nichts zu wollen.

Die Parabel, der Exot unter den Kegelschnitten, ist also der interessante Fall.

13    Zirkel und Lineal

Die Kegelschnitte kšnnen punktweise mit Zirkel und Lineal konstruiert werden. FŸr die Parabel benštigen wir eine Gerade (Leitlinie) und einen Punkt (Brennpunkt). Die Abbildung 20 illustriert exemplarisch die Konstruktionen von zwei Punkten. Die jeweils gleichfarbigen AbstŠnde sind gleich gro§.

 

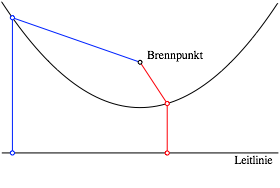
Abb. 20: Konstruktion von Parabelpunkten

 

Die Tangenten ergeben sich als Mittelsenkrechte (Abb. 21).

 

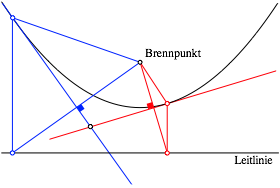
Abb. 21: Tangenten als Mittelsenkrechte

 

In unserem Beispiel aus der Faltgeometrie (Abb. 6) spielen der Punkt die Rolle des Brennpunktes und die untere Papierkante die Rolle der Leitlinie.

Die rechten Winkel in der Abbildung 21 liegen auf der Scheiteltangente der Parabel (Abb. 22). Dabei erkennen wir auch wieder die Winkeleisen der Abbildung 9.

 

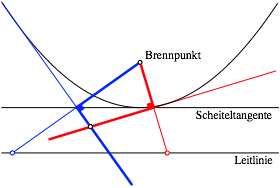
Abb. 22: Scheiteltangente und Winkeleisen

 

Damit schlie§t sich der Gedankenkreis.

 

14    Sehnenvierecke

Der im Abschnitt 5 vorgestellte Beweis lŠsst sich auch mit Sehnenvierecken durchfŸhren. Die Idee dazu verdanke ich Emese Vargyas, Mainz.

Die Abbildung 23 entspricht der Abbildung 10; das Koordinatensystem ist weggelassen. Wegen der rechten Winkel bei A und B ist das Viereck SAFB ein Sehnenviereck (Abb. 23a). In der Abbildung 23b ist zusŠtzlich das Sehnenviereck CAFB eingezeichnet.

In diesem Sehnenvierck gilt . Dabei ist s auch der Abstand von S von der Geraden AB.

 

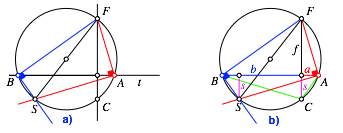
Abb. 23: Sehnenviereck

 

In der Abbildung 24 sind nun drei blaue rechte Winkel eingetragen.

 

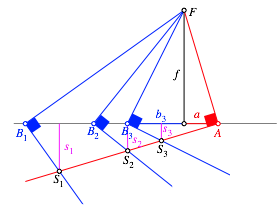
Abb. 24: Drei blaue rechte Winkel

 

Dabei gilt:

 

 

Somit ist auch:

 

 

Das TeilverhŠltnis auf dem roten Schenkel ist also unabhŠngig von der Position des Punktes A.

FŸr diese †berlegungen benštigen wir die gewšhnlichen StrahlensŠtze.

 

Last modified: 16. Juni 2015