Hans Walser

Das DIN-Format und der Raum

Hochrheinseminar Waldshut

Freitag, 14. November 2014, 15-16.30 Uhr

Musiksaal des Hochrhein-Gymnasiums Waldshut

Zusammenfassung

Das bekannte DIN Format, zum Beispiel Papier im Format DIN A4 oder DIN A6, hat viele interessante geometrische Eigenschaften. Diese Papiere können auch für den Bau räumlicher Modelle verwendet werden. Zudem lässt sich die Idee des DIN Formates auf andere Figuren übertragen.

1 Diagonalen

Wir beginnen mit zwei Papieren im DIN A4 Format und falten eines zum DIN A5 Format. Dann zeichnen wir in beiden die Diagonale von links unten nach rechts oben und legen sie so aufeinander, dass die Ecken links unten bündig sind. Dann liegen die Diagonalen in einer Flucht.

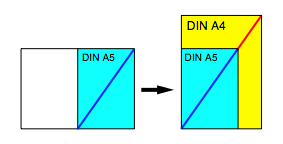
Es passt

Nun vergleichen wir mit dem in den USA gebräuchlichen Papierformat US Letter. Dieses Papier ist im Vergleich zu DIN A4 etwas weniger hoch, dafür etwas breiter.

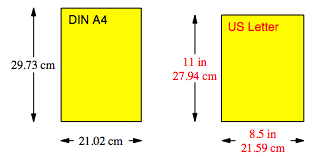
DIN A4 und US Letter

Zur Erinnerung: 1 in (inch) = 2.54 cm

Im US Letter Format stimmen die Diagonalen nicht überein.

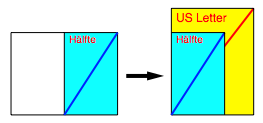
Diagonalen passen nicht aufeinander

2 Länge und Breite

2.1 DIN Format

Die Tabelle zeigt Länge (Höhe) und Breite aufeinanderfolgender DIN Formate. Es wurde auch das Verhältnis Länge zu Breite angegeben. Wir sehen, dass da, abgesehen von kleinen Mess- und Rundungsfehlern, immer dieselbe Verhältniszahl herauskommt. Das heißt, dass die DIN Formate alle dieselbe Form haben. Lediglich die Größe ändert, sie werden immer kleiner.

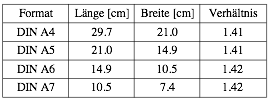
Ausmaße im DIN Format

Was für eine Zahl ist diese Verhältniszahl?

Dazu folgende Rechnungen:

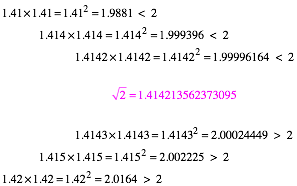
Die Zahl ist die Quadratwurzel aus 2 oder kurz „Wurzel 2“. Das ist die Zahl, welche mit sich selber multipliziert genau 2 ergibt. Diese Zahl ist recht interessant. Sie hat unendlich viele Dezimalstellen und keine Periode (Wiederholungen) in den Dezimalstellen.

2.2 US Letter

Die Tabellen geben die Ausmaße für das US Letter Format zunächst in cm und dann in inch.

Ausmaße im US Letter Format

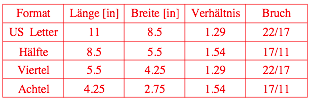
Ausmaße in inch

Wir sehen, dass wir im Wechsel zwei verschiedene Verhältniszahlen haben. Die Formen ändern sich. Das US Letter Format ist zunächst kurz und breit, die Hälfte davon aber ein langer Lulatsch.

Die beiden Verhältniszahlen lassen sich aber als schöne Brüche darstellen. Die Elftel haben eine Periodenlänge 2:

Bei den Siebzehnteln ist die Sache spannender: die Periodenlänge ist 16. Das kann man nicht mehr mit dem Taschenrechner, man muss von Hand arbeiten. Es ergibt sich:

3 Quadrat und Quadratdiagonale

Durch Falten erhalten wir ein Quadrat mit einer Diagonalen.

Quadrat mit einer Diagonale

Die lange Seite des DIN Papieres ist gleich lang wie die Quadratdiagonale. Beim US Letter Papier passt es nicht.

Bei DIN A4 passt es, bei US Letter nicht

Nun schneiden wir das Quadrat ab. Wir werden es später noch brauchen können. Mit vier Reststücken (Teamwork) können wir ein regelmäßiges Achteck bauen, wenn wir die Stücke immer diagonal aufeinanderlegen.

Quadrat. Achteck aus 4 Reststücken

4 Spirale

Wir schneiden ein Set von DIN Papieren zu. Dies geschieht durch fortlaufendes flächenmäßiges Halbieren.

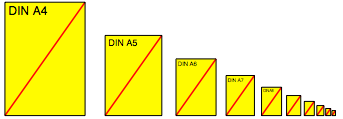
Set von DIN Papieren

Wir können die Papiere so anordnen, dass sie in ein DIN A3 Format passen.

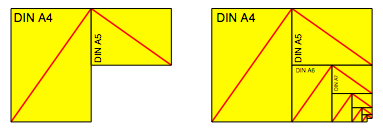
Ausfüllen eines DIN A3 Formates

Wir können die Papiere aber auch spiralförmig anordnen.

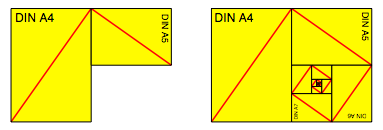
Eckige Spirale

Das Zentrum der Spirale ergibt sich durch Dritteln. Das ist merkwürdig, weil wir bis jetzt immer flächenmäßig halbiert haben.

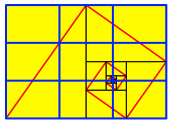
Zentrum bei Dritteln

5 Die DIN Idee

Die Grundidee des DIN Formates besteht darin, dass wir ein Papier in zwei Teile zerlegen können, welche die gleich Form haben wir das Startpapier.

Gibt es andere Figuren, welche in zwei Teile zerlegt werden können, so dass die Form erhalten bleibt?

5.1 Das halbe Quadrat

Wir zerschneiden unser Quadrat längs der Diagonalen. Dadurch erhalten wir zwei so genannte rechtwinklig gleichschenklige Dreiecke.

Das rechtwinklig gleichschenklige Dreieck können wir nun zerlegen in zwei kleinere rechtwinklig gleichschenklige Dreiecke. Eines der beiden kleinen Dreiecke können wir weiter zerlegen und so weiter.

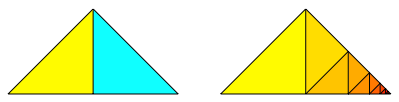
Halbes Quadrat

Es gibt auch eine spiralförmige Anordnung. Das Zentrum der Spirale liegt bei Fünfteln.

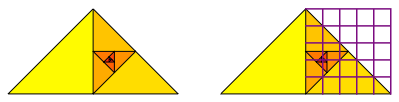
Spirale

Wir können in beiden Fällen die Thaleskreise einzeichnen.

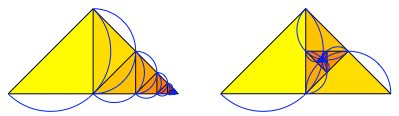
Thaleskreise

Die Spirale können wir auch erfalten. Dazu starten wir mit einem großen rechtwinklig gleichschenkligen Papier. Besonders schön wird es, wenn das Papier auf seinen zwei Seiten ungleich gefärbt ist.

Faltmodell

5.2 DIN Kisten

Statt mit zweidimensionalen rechteckigen Papieren arbeiten wir nun mit dreidimensionalen Kisten (Quadern). Für die Seitenverhältnisse brauchen wir nun kubische Wurzeln aus 2.

Es ist:

Die kubische Wurzel aus 2 hat ebenfalls unendlich viele Dezimalstellen und nie eine Periode.

Durch volumenmäßiges Halbieren einer Kiste erhalten wir zwei Kisten von der gleichen Form von der nächsten Generation.

Wir können das Kistenset aufeinander stapeln.

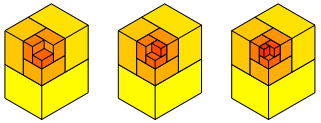
Kisten nach der DIN Idee

Auch hier können wir nach einer Spirale fragen. Das Interessante ist, dass sie bereits da ist. Man muss sie nur sehen.

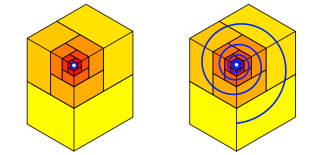
Spirale

Es handelt sich um eine räumliche Spirale nach Art einer Wasserschnecke. Von oben sieht sie wie eine ebene Spirale aus, aber in der Seitenansicht sehen wir, dass sie sich in den Raum hineinschraubt.

Wasserschnecke

Die Foto zeigt eine versteinerte Schnecke aus dem Jura.

Versteinerte Schnecke

6 Wir falten ein Achteck

Wir arbeiten mit einem DIN A4 Papier. Die Abbildung zeigt die einzelnen Faltschritte.

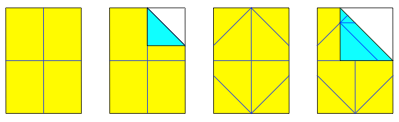
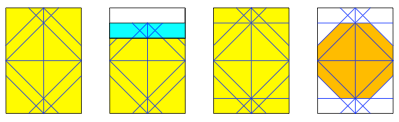
Faltschritte für das Achteck

Die Foto zeigt Vorder- und Rückseite des Faltmodells.

Achteck als Faltmodell

Wenn wir denselben Faltprozess mit einem Papier im US Letter Format durchführen, erhalten wir zwar auch ein Achteck mit gleichen Winkeln, aber die Seiten sind im Wechsel kurz oder lang. Es ist kein regelmäßiges Achteck.

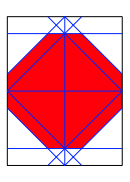
Achteck aus US Letter

7 Würfel und Tetraeder

7.1 Kantenmodell des Würfels

Als Baumaterial dient Papier im DIN A6 Format. Geeignet ist Papier der Stärke 80 g/m², das vom Format DIN A4 auf DIN A6 zugeschnitten wird. Ebenfalls geht es mit dünnen Karteikarten.

Für jede Kante braucht es ein Papier.

Für den Faltprozess verwenden wir eine etwas festere DIN A6 Karte als Faltlehre. Wir legen diese Faltlehre diagonal auf ein DIN A6 Papier und falten die vorstehenden Ecken des darunterliegenden Papiers nach vorne über die Faltlehre. Dann entfernen wir die Faltlehre. Der Umriss des Papiers ist nun ein Rhombus mit dem spitzen Winkel .

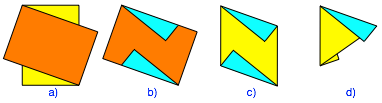
Faltvorgang

Nun falten wir die untere Spitze des Rhombus nach hinten unter die obere Spitze. Diese letzte Faltlinie wird zu einer Kante des Würfels. Was an dieser Kante noch vorsteht, kann zurückgebogen oder abgeschnitten werden. Damit haben wir unser Bauteil. Es hat die Form eines doppellagigen gleichschenkligen Dreiecks mit zwei Verbindungslaschen zum Einschieben in die Nachbarteile.

Die folgende Abbildung zeigt ein geöffnetes Bauteil von innen. Die Spitzen der beiden Rhomben-Hälften müssen vor dem Zusammenbau des Modells noch aufeinander gelegt werden. Diese Spitzen kommen alle in den Mittelpunkt des Würfels zu liegen. Die Seiten der Rhomben werden zu halben Raumdiagonalen des Würfels.

Wir benötigen 12 Bauteile. Beginnend mit drei verschieden farbigen DIN A4 Papieren, die wir zu DIN A6 Papieren vierteln, erhalten wir drei Sätze von je vier gleichfarbigen Bauteilen. Damit können wir den jeweils vier parallelen Würfelkanten dieselbe Farbe zuordnen.

Bauteil

Und nun kommt das Interessante, der Zusammenbau. Wir schieben jeweils eine Verbindungslasche zwischen die beiden gleichschenkligen Dreiecke des Nachbarbauteils. Dabei achten wir darauf, dass an jeder halben Raumdiagonale des Würfels drei Bauteile in den drei verschiedenen Farben zusammen kommen. Parallele Würfelkanten haben dieselbe Farbe.

Kantenmodell des Würfels

Es empfiehlt sich, den Zusammenbau schrittweise mit Büroklammern zu fixieren. An jeder Ecke des Würfels ergeben sich schließlich drei Büroklammern.

Wenn alles sitzt, können die Büroklammern schrittweise entfernt und durch eine Heftklammer mit dem Tacker ersetzt werden. Dabei hat man den Ehrgeiz, dass die Klammern symmetrisch eingebracht werden.

7.2 Kantenmodell des Tetraeders

Beim regelmäßigen Tetraeder haben wir den Ergänzungswinkel von auf 180°, also 109.4712°, als Winkel zwischen den vom Zentrum aus zu den Ecken verlaufenden Strecken. Daher kann analog zum Kantenmodell des Würfels ein Kantenmodell des Tetraeders gebaut werden.

Kantenmodell des Tetraeders

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Last modified 17. Oktober 2014