Berhrungen
Hans Walser
17.-19. Mrz 2016
19. Forum fr Begabungsfrderung in Mathematik
FH Sdwestfalen in Soest
Mit einfachen Modellen und/oder dynamischer Geometriesoftware lassen sich verschiedene klassische Berhrprobleme verblffend einfach angehen.
Zur Sprache kommen Inkreise, das Problem des Apollonius, Tangentenvierecke in der Ebene und im Raum, Parittsfragen.
1 Gr§ter Sehwinkel
1.1 Das Problem
Ein
Fahrzeug fhrt auf einer Stra§e in Richtung von x an einem Verkehrsschild der Breite b vorbei, das im Abstand a
von der Fahrtrichtung steht (Abb. 1). Wann ist der Sehwinkel ![]() ,
unter dem das Schild erscheint, am gr§ten? (Rhenbeck 2015), [Sehwinkelproblem]
,
unter dem das Schild erscheint, am gr§ten? (Rhenbeck 2015), [Sehwinkelproblem]
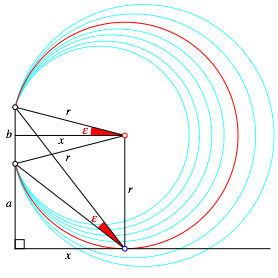
Abb. 1: Optimaler Sehwinkel
1.2 Lsung mit Berhrung
Unter allen Ortsbogen ber der Strecke b suchen wir den kleinsten (entspricht dem gr§ten Winkel), der die Fahrtrichtung gerade noch erreicht, also tangential dazu ist.
Dieser
Ortsbogen hat den Radius ![]() und kann daher sehr einfach konstruiert
werden. Damit ist die Aufgabe konstruktiv gelst.
und kann daher sehr einfach konstruiert
werden. Damit ist die Aufgabe konstruktiv gelst.
2 Inkreis im Dreieck
2.1 Winkelhalbierende
Der Inkreis wird in der Regel mit Winkelhalbierenden konstruiert.
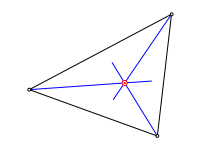
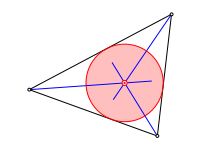
Winkelhalbierende und Inkreis
Es geht aber auch ohne Winkelhalbierende.
2.2 Kegel und Lochschablone
Wir stlpen eine Lochschablone des Dreiecks ber einen geraden Kreiskegel. Am Anschlag zeigt sich der Inkreis.

Kegel und Lochschablone
2.3 Schlie§ungsfigur
Wir zeichnen Kreisbgen ins Dreieck. Die Figur schlie§t sich nach sechs Schritten.
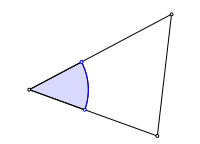
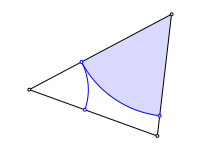

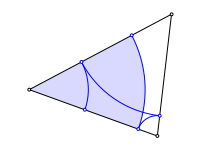

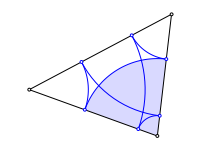
Schlie§ungsfigur
Die sechs Punkte auf den Dreiecksseiten liegen auf einem Kreis. Dieser ist konzentrisch zum Inkreis.
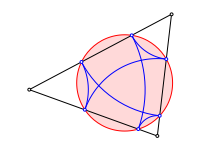
Sechspunktekreis
2.4 Besserer Startpunkt
Wir verschieben den Startpunkt etwas.
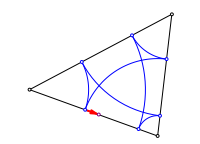
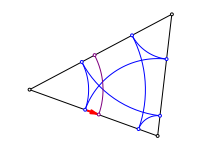
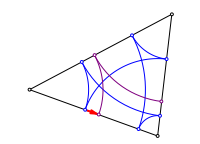
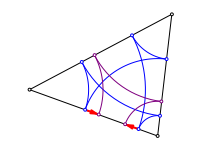
Die Knigskinder kommen sich nher
Nach drei Schritten haben wir dieselbe Verschiebung in der entgegengesetzten Richtung. Die beiden Punkte nhern sich an.
Beim Startpunkt in der Mitte schlie§t sich die Figur schon nach drei Schritten. Es ergeben sich die Berhrpunkte des Inkreises.
Diese Denkweise wurde von Adam Ries (1492/93-1559) als regula falsi (Regel des falschen Ansatzes) kultiviert.
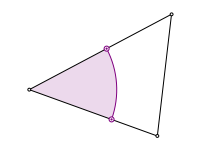
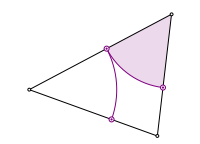
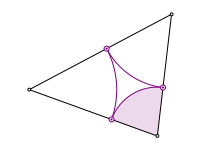
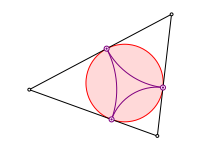
Optimaler Startpunkt. Inkreis
2.5 Zwischenspiel: Gleichdick
Wir beginnen mit einem Startpunkt au§erhalb einer Dreiecksseite und bgeln durch. Die Figur schlie§t sich wiederum nach sechs Schritten.


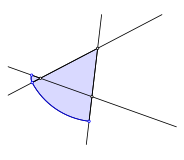
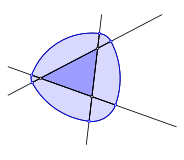
Startpunkt au§en
Die entstehende Figur ist ein Gleichdick. Sie hat berall denselben Durchmesser. Die Gleichdicke werden auch als Orbiforme (Kreisartige) bezeichnet. Der bekannteste Sonderfall ist das Reuleaux-Dreieck.
Die Mittelpunkte der Durchmesser auf den Dreiecksseiten sind die Berhrpunkte des Inkreises. Die Figurenfolge zeigt die Invarianz des Durchmessers.
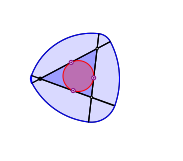
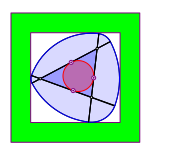
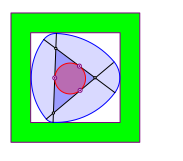
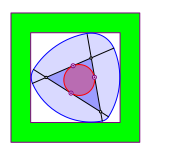
Gleichdick
2.6 Inkreis mit Hyperbeln
Wir zeichnen eine Hyperbel mit zwei Dreiecksecken als Brennpunkte, welche durch die dritte Ecke verluft. Dies geht auf drei Arten. Die drei Hyperbeln schneiden sich in einem Punkt und durchsetzen die Dreiecksseiten rechtwinklig. Die Schnittpunkte mit den Dreiecksseiten sind die Berhrpunkte des Inkreises. Beweise als bungsaufgabe.
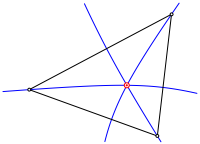
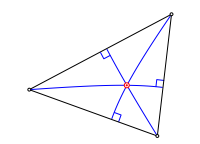
Hyperbeln
Der Schnittpunkt der drei Hyperbeln ist allerdings nicht das Zentrum des Inkreises, aber das Zentrum des Kreises, der die drei Kreisbgen der frheren Konstruktion berhrt.
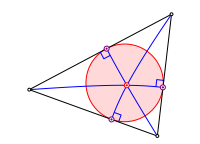
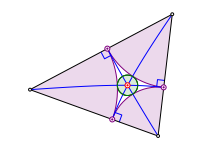
Inkreis und Innenkreis
2.7 Ellipsen
Exemplarisch arbeiten wir nun mit Ellipsen. Wir zeichnen zwei Ellipsen, die je zwei Dreiecksecken als Brennpunkte haben und durch die jeweilige dritte Ecke verlaufen.
Zustzlich zeichnen wir das Hyperbelpaar mit den beiden dritten Ecken als Brennpunkten und durch die erste Ecke.
Wir erhalten zwei Schnittpunkte und die Berhrpunkte eines Ankreises.
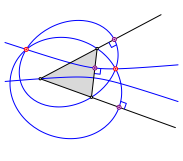
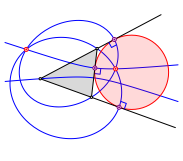
Ellipsen fhren zu einem Ankreis
2.8 Zwischenspiel: Problem des Apollonius
Apollonius von Perge (ca. 262 v. Chr. – ca. 190 v. Chr.): Zu drei Kreisen ist ein vierter Kreis gesucht, der die drei gegebenen Kreise berhrt.
Dazu zeichnen wir erst die Mittelpunkte der drei Minimalabstnde. Ein geeigneter Kreis um einen solchen Mittelpunkt berhrt zwei der drei gegebenen Kreise. Wir der Kreisradius etwas vergr§ert, wandert der Mittelpunkt auf der Hyperbel mit den Brennpunkten in den Zentren der beiden berhrten Kreise.
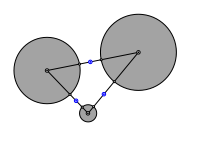
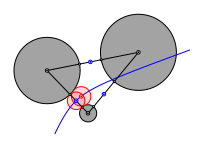
Minimalabstnde. Hyperbel
Die drei nach dieser berlegung konstruierten Hyperbeln schneiden sich in einem Punkt. Dieser ist der Mittelpunkt des gesuchten Kreises.
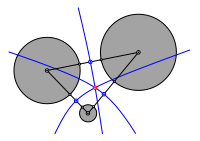
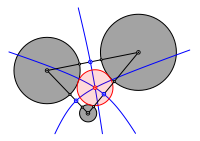
Problem des Apollonius
Diese Konstruktion geht auf Adriaan van Roomen (1561-1615) zurck.
Puritaner werden bei dieser Konstruktion die Nase rmpfen. Sie ist nicht mit Zirkel und Lineal durchfhrbar. Allerdings ist da zu bemerken, dass Konstruktionen mit ãZirkel und LinealÒ auch nur in unserer Vorstellung exakt sind. Die Konstruktion von van Roomen ist aber rein logisch vllig exakt. Mit heutigen technischen Mglichkeiten (DGS) ist auch ein hinreichend gute Zeichnung mglich.
Bei einer anderen Disposition der drei gegebenen Kreise muss auch mit Ellipsen gearbeitet werden.
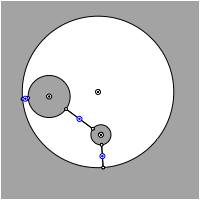
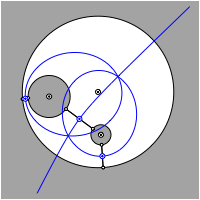
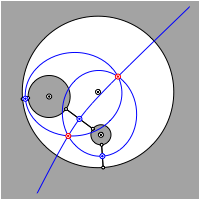
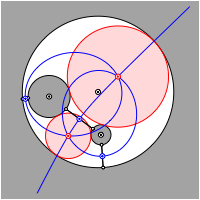
Konstruktion mit Ellipsen
3 Vierecke
3.1 WennÕs nicht geht, gehtÕs nicht
Wenn wir bei einem beliebigen Viereck Bgen einzeichnen und den Startpunkt verschieben, verschiebt sich der Endpunkt um gleich viel in der gleichen Richtung. Die Knigskinder kommen also nicht zusammen.

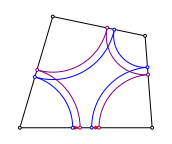
Die Knigskinder kommen sich nicht nher
3.2 Tangentenviereck
Wenn wir umgekehrt in einem Tangentenviereck Bgen einzeichnen, schlie§t sich die Bogenfigur bei beliebigen Startwerten nach vier Schritten.
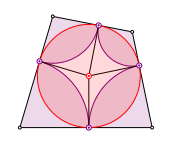
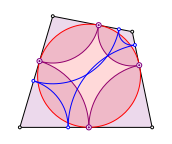
Tangentenviereck
Da die von einer Ecke ausgehenden Tangentenabschnitte jeweils gleich lang sind, erhalten wir fr ein Tangentenviereck die notwendige Bedingung, dass die Summe der Gegenseiten konstant ist.

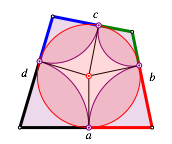
Summe der Gegenseiten konstant
Es gilt:
![]() (1)
(1)
quivalent dazu verschwindet die alternierende Seitensumme:
![]() (2)
(2)
Schlie§lich gibt es auch eine Differenzengleichheit:
![]() (3)
(3)
Man kann zeigen, dass diese notwendigen Bedingungen fr ein Tangentenviereck auch hinreichend sind. Die Bedingungen legen allerdings das Tangentenviereck noch nicht fest.
3.3 Gelenkmodelle
Ein Gelenkmodell, das einer dieser Bedingungen gengt, kann verformt werden. In jeder Situation ergibt sich ein Tangentenviereck.



Verformungen
Den gr§ten Inkreis und damit auch den gr§ten Flcheninhalt erhalten wir fr dasjenige Viereck, das auch einen Umkreis hat (Sehnentangentenviereck). Es handelt sich hier um eine Variante des isoperimetrischen Problems.
Die folgende Abbildung zeigt ein echtes Gelenkmodell in zwei verschiedenen Positionen. Die Tangentenviereckbedingung kann durch Abzhlen der Lochabstnde verifiziert werden.

Gelenkmodell
Die optimale Position finden wir, indem wir das Modell ber einen Kegel stlpen.


Optimale Lsung
Die Bedingung (2) (Verschwinden der alternierenden Seitensumme) gestattet, das Gelenkmodell wie ein Taschenmesser zusammenzuklappen.


Klappviereck
Wir knnen ein geschlossenes Papierband flachdrcken und erhalten so ein Gelenkmodell eines Tangentenviereckes.


Papierband flachdrcken
Dies fhrt schlie§lich zu einem Gelenkmodell aus Kartonstreifen, das nicht mit Scherengelenken arbeitet, sondern mit Bandscharnieren.


Modell aus Kartonstreifen
3.4 Vier Mnzen
Die Zentren von vier aneinandergeschobenen Mnzen bilden ein Tangentenviereck.

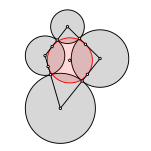
Vier Mnzen
3.5 Konstruktion mit einer Hyperbel
Die Bedingung (3) fhrt zu einer Konstruktion mit einer Hyperbel. Die beiden Brennpunkte und zwei Hyperbelpunkte bilden ein Tangentenviereck.

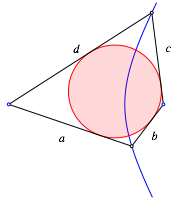
Konstruktion mit einer Hyperbel
3.6 Abstand von Berhrpunkten
Wir unterteilen ein Rechteck mit einer Diagonalen in zwei Dreiecke und zeichnen in jedem Teildreieck den Inkreis.
Wie gro§
ist der Abstand ![]() der beiden
Berhrpunkte auf der Diagonale?
der beiden
Berhrpunkte auf der Diagonale?
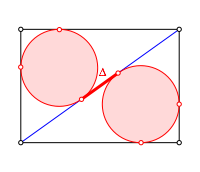
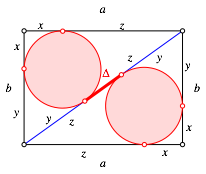
Abstand zwischen den Berhrpunkten?
Mit den angegebenen Bezeichnungen fr die Tangentenabschnitte ist zunchst:
![]() (4)
(4)
Weiter ist:
![]() (5)
(5)
Der gesucht Abstand ist also gleich der Differenz der Rechteckseiten.
In einem beliebigen Viereck knnen wir analog mit Tangentenabschnitten arbeiten.
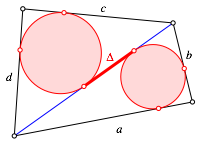
Beliebiges Viereck
Wir erhalten:
![]() (6)
(6)
Das hei§t
aber, dass in einem Tangentenviereck der Abstand ![]() verschwindet. Die Inkreise der beiden
Teildreiecke berhren sich.
verschwindet. Die Inkreise der beiden
Teildreiecke berhren sich.
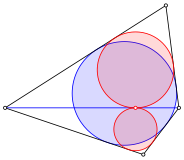
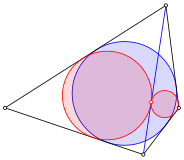
Der Abstand verschwindet
4 Im Raum: Tangententetraeder
Die folgende Abbildung zeigt ein Tetraeder mit einer Kugel, welche alle sechs Kanten des Tetraeders berhrt.
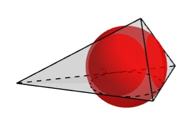
Tangententetraeder
Einzeichnen der Berhrungspunkte und Weglassen der Kantenberhrkugel fhrt zur Einsicht dass die Summen der Gegenkanten konstant sind.
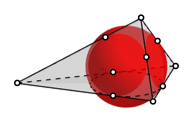
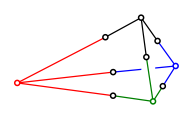
Summen der Gegenkanten konstant
Die folgende Abbildung zeigt die Abwicklung des Tangententetraeders.
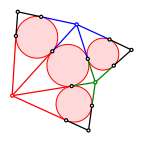
Abwicklung
Zwei Seitendreiecke mit einer gemeinsamen Kante bilden in der Abwicklung ein Tangentenviereck.
5 Fnfeck
5.1 Bogen
In einem beliebigen Fnfeck zeichnen wir die Eckenbogen ein.
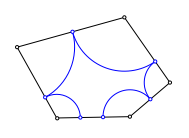

Im Fnfeck
Wir haben im Prinzip dieselbe Situation wie beim Dreieck. Trotzdem hat das Fnfeck nicht automatisch einen Inkreis. Es ist sozusagen erst die notwendige Bedingung dafr automatisch erfllt.
Die folgende Abbildung zeigt die Bgen fr ein Gelenkfnfeck. Es sind zustzlich die erwarteten Berhrungspunkte mit einer Musterttenklammer markiert. Diese Klammern sind also keine Gelenke.


Gelenkmodell
5.2 Tangentenfnfeck
Erst wenn wir das Gelenkmodell ber den Kegel strammstlpen, ergibt sich das Tangentenfnfeck.


Tangentenfnfeck
5.3 Tangentenpentagramm
Mit denselben Bauteilen des Gelenkmodells in derselben Reihenfolge und denselben Berhrungspunkten, aber mit doppeltem Umlauf, ergibt sich ein Tangentenpentagramm.

Weihnachten kommt bestimmt
6 Berechnungen
Wir fhren die Berechnungen exemplarisch am Fnfeck durch.
In einem ersten Schritt berechnen wir die Tangentenabschnitte, also die Radien der violetten Bgen.
Im zweiten Schritt berechnen wir den Inkreisradius des Tangentenfnfeckes.
6.1 Tangentenabschnitte
Wir verwenden die Bezeichnungen der folgenden Figur.
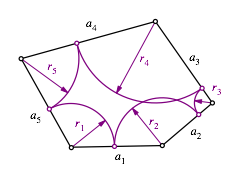
Bezeichnungen
Es ist:
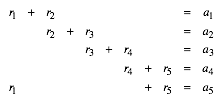 (7)
(7)
Durch alternierendes Addieren der Zeilen von (7) ergibt sich:
![]() (8)
(8)
Mit zyklischer Vertauschung erhalten wir:
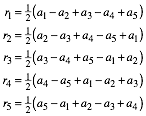 (9)
(9)
Das Gleichungssystem (7) hat die Koeffizientenmatrix:
 (10)
(10)
Fr die
Determinanten der quadratischen ![]() Matrix
links erhalten wir exemplarisch:
Matrix
links erhalten wir exemplarisch:
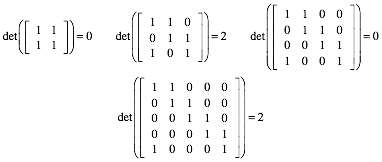 (11)
(11)
Es ergibt sich eine Fallunterscheidung gem§ der Paritt von n:
Fr ungerades n erhalten wir die Determinante 2. Dies kann zum Beispiel mit der Entwicklung nach der ersten Spalte gezeigt werden. Das Gleichungssystem ist regulr und hat genau eine Lsung.
Fr gerades n erhalten wir die Determinante 0. Die alternierende Zeilensumme verschwindet. Wir sind im singulren Fall. Wenn die alternierende Summe der Koeffizienten nicht verschwindet, haben wir keine Lsung. Sonst unendlich viele Lsungen.
6.2 Inkreisradius
Fr die Berechnung des Inkreisradius r arbeiten wir gem§ der folgenden Abbildung.
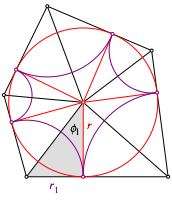
Berechnung
des Inkreisradius r
Es ist zunchst:
![]() (11)
(11)
Analog
fr die brigen Sektoren. Da jeder Winkel ![]() zweimal vorkommt,
ist:
zweimal vorkommt,
ist:
![]() (12)
(12)
Somit erhalten wir fr den Inkreisradius r die Bestimmungsgleichung:
![]() (13)
(13)
Im Beispiel unseres Gelenkmodells hei§t das:
![]() (14)
(14)
Mit CAS erhalten wir die Lsung:
![]() (15)
(15)
Das Pentagramm-Gelenkmodell hat die doppelte Umlaufszahl. Anstelle der Gleichung (14) erhalten wir daher:
![]() (16)
(16)
Diese Gleichung hat die Lsung:
![]() (17)
(17)
Literatur
Rhenbeck, Christian (2015): Sehwinkelproblem. MNU Der mathematische und naturwissenschaftliche Unterricht 68/5 (15. 9. 2015), S. 308-309.
Websites
[Sehwinkelproblem], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/S/Sehwinkelproblem/Sehwinkelproblem.htm
www.walser-h-m.ch/hans/Miniaturen/S/Sehwinkelproblem/Sehwinkelproblem.pdf
[Tangentenfnfeck], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/T/Tangentenfuenfeck/Tangentenfuenfeck.htm
www.walser-h-m.ch/hans/Miniaturen/T/Tangentenfuenfeck/Tangentenfuenfeck.htm
[Tangentensiebeneck], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/T/Tangentensiebeneck/Tangentensiebeneck.htm
www.walser-h-m.ch/hans/Miniaturen/T/Tangentensiebeneck/Tangentensiebeneck.pdf
[Tangententetraeder], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/T/Tangententetraeder/Tangententetraeder.htm
www.walser-h-m.ch/hans/Miniaturen/T/Tangententetraeder/Tangententetraeder.pdf
[Tangentenviereck als Gelenkmodell], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/T/Tang_Viereck_Gelenkmodell/Tang_Viereck_Gelenkmodell.htm
www.walser-h-m.ch/hans/Miniaturen/T/Tang_Viereck_Gelenkmodell/Tang_Viereck_Gelenkmodell.pdf
[Tangentenviereck mit Mnzen], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/T/Tang4eck_m_Muenzen/Tang4eck_m_Muenzen.htm
www.walser-h-m.ch/hans/Miniaturen/T/Tang4eck_m_Muenzen/Tang4eck_m_Muenzen.pdf
[Tangentenvierecke], abgerufen 20. 11. 2015
www.walser-h-m.ch/hans/Miniaturen/T/Tangentenvierecke/Tangentenvierecke.htm
www.walser-h-m.ch/hans/Miniaturen/T/Tangentenvierecke/Tangentenvierecke.pdf
Adresse des Autors:
Hans Walser
hwalseratbluewin.ch
www.walser-h-m.ch/hans/