Hans Walser, [20240409]
14-Eck
1 Worum es geht
Das regelmäßige Siebeneck und das regelmäßige 14-Eck lassen sich nicht mit Zirkel und Lineal konstruieren
Es gibt eine Einschiebekonstruktion für das regelmäßige 14-Eck
Rhombenfiguren
2 Konstruktionsvorgang
Wir beginnen mit einem rechtwinkligen Dreieck (Abb. 1), dessen eine Kathete recht kurz und die andere recht lang ist.

Abb. 1: Startdreieck
In diesem Dreieck tragen wir, bei der Ecke mit dem rechten Winkel beginnend, die Länge der kurzen Kathete sechsmal im Wechsel auf der Hypotenuse und der langen Kathete ab (Abb. 2). Zusammen mit der kurzen Kathete ergibt dies einen Zickzackweg mit sieben gleich langen Teilstrecken.
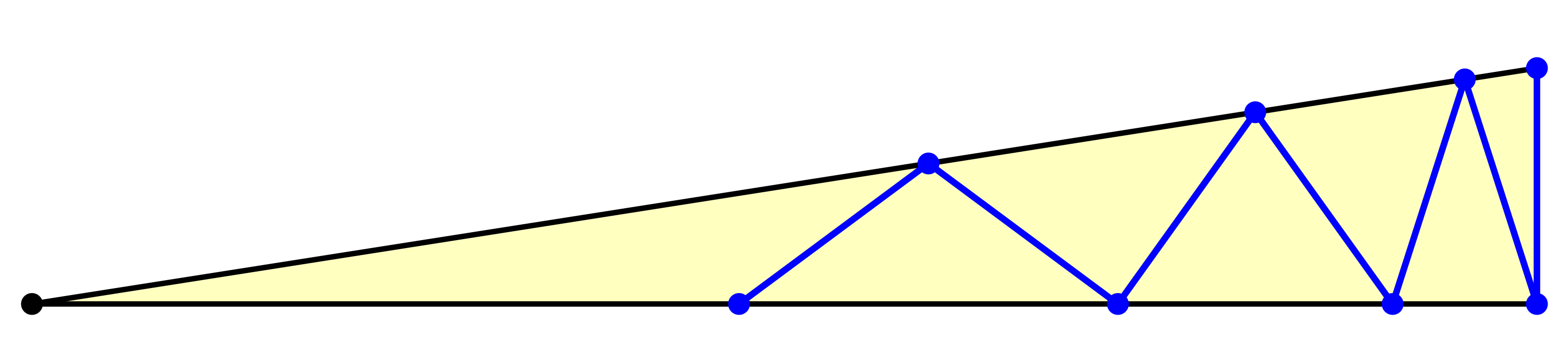
Abb. 2: Zickzackweg
Und nun kommt der Einschiebevorgang. Wir verkürzen die lange Kathete, bis das Ende des Zickzackweges auf die Dreiecksecke zu liegen kommt (Abb. 3).
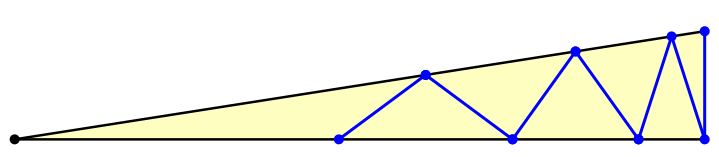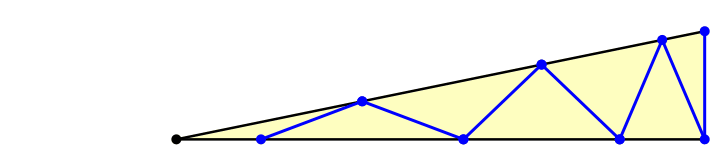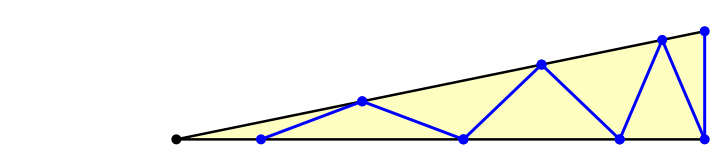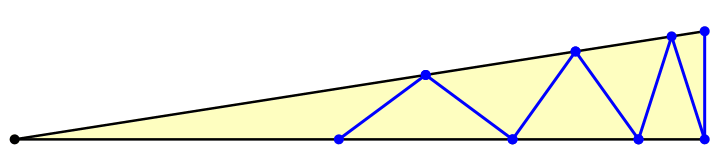
Abb. 3: Einschieben
Die Abbildung 4 zeigt die Endlage.
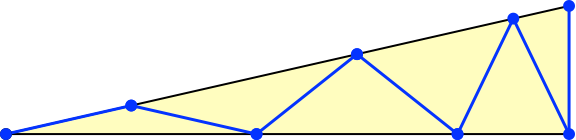
Abb. 4: Endlage
3 Winkelberechnung
In der Endlage misst der kleinere der beiden spitzen Dreieckswinkel π/14. Dies kann eingesehen werden wie folgt.
Den kleineren der beiden spitzen Dreieckswinkel bezeichnen wir mit β. Der Zickzackweg unterteil das rechtwinklige Dreieck in sechs gleichschenklige Dreiecke (Abb. 5).
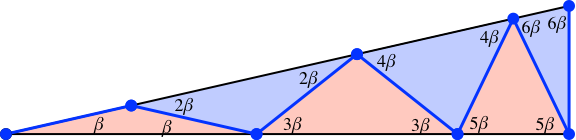
Abb. 5: Unterteilung in gleichschenklige Dreiecke
Für die Basiswinkel dieser gleichschenkligen Dreiecke erhalten wir der Reihe nach β, 2β, 3β, 4β, 5β, 6β. Es gilt folgende Regel: Basiswinkel eines Dreiecks = Summe der beiden Basiswinkel des vorhergehenden Dreiecks minus Basiswinkel des vorvorhergehenden Basiswinkels. Wir haben die Rekursion
fn+1 = 2fn – fn–1
mit den beiden Startwerten f0 = 0 und f1 = β.
Wir haben somit eine verallgemeinerte Fibonacci-Rekursion, welche merkwürdigerweise eine arithmetische Folge ergibt.
Die beiden spitzen Winkel des rechtwinkligen Dreiecks messen also β und 6β. Somit ist:
β + 6β = π/2
β = π/14
Damit sind wir auf der Butterseite.
4 Spiegeln
Wir spiegeln das rechtwinklige Dreieck an der langen Kathete (Abb. 6). Aus den gleichschenkligen Dreiecken werden Rhomben.
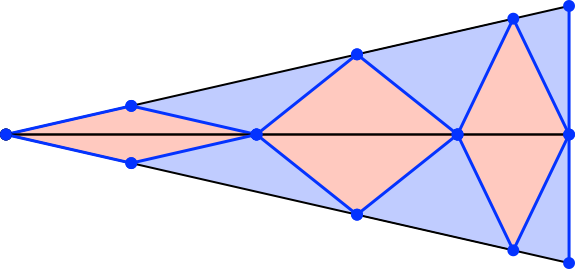
Abb. 6: Spiegeln
Weiterspiegeln (jetzt an der ehemaligen Hypotenuse) führt zu einem durch Rhomben unterteilten regelmäßigen 14-Eck (Abb. 7).

Abb. 7: Regelmäßiges 14-Eck
Lehrer Lämpel: Wenn wir nur jede zweite Ecke nehmen, haben wir ein regelmäßiges Siebeneck.
5 Das 14-Eck im 14-Eck
Wir erkennen halb so große 14-Ecke, eines davon ist in der Abbildung 8 markiert.

Abb. 8: 14-Eck im 14-Eck
Wir können dieses ausstanzen und verdreht wieder einsetzen (Abb. 9).

Abb. 9: Ausstanzen und verdreht einsetzen
Dies gibt Anlass zu einer Figurenfolge (Abb. 10).

Abb. 10: Figurenfolge
Weblinks
Hans Walser: Lineare
Fibonacci-Folge
https://walser-h-m.ch/hans/Miniaturen/L/Lineare_Fibonacci-Folge/Lineare_Fibonacci-Folge.html