1 Worum es geht

Eine Gleichmäßigkeitsbedingung in einer Figur mit einem regelmäßigen Sechseck und einem gleichseitigen Dreieck führt auf den Goldenen Schnitt.

Rationale Flächenbeziehung.

2 Das Dreieck im Sechseck

In ein regelmäßiges Sechseck zeichnen wir ein gleichseitiges Dreieck (Abb. 1). Eine Ecke des Dreiecks liegt in einer Ecke des Sechsecks. Eine zweite Ecke liegt auf der übernächsten Sechseckseite. Die dritte Ecke liegt dann auf einer Diagonalen des Sechsecks.

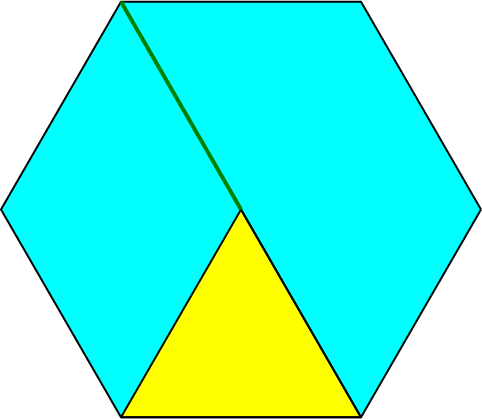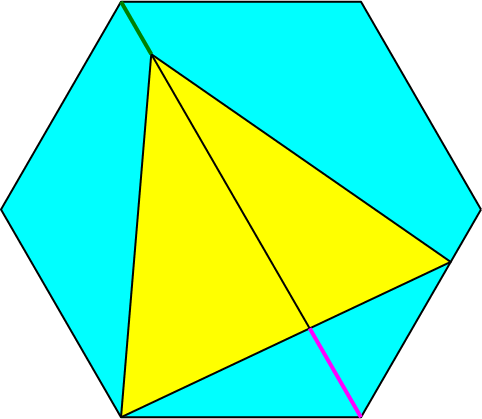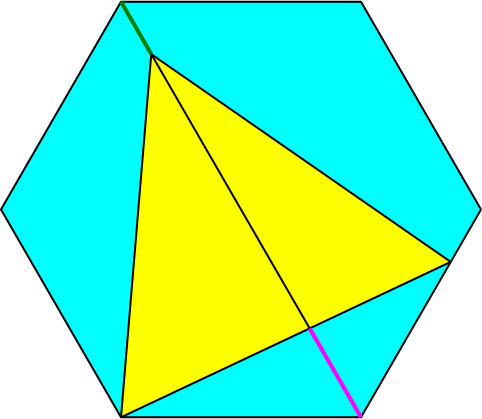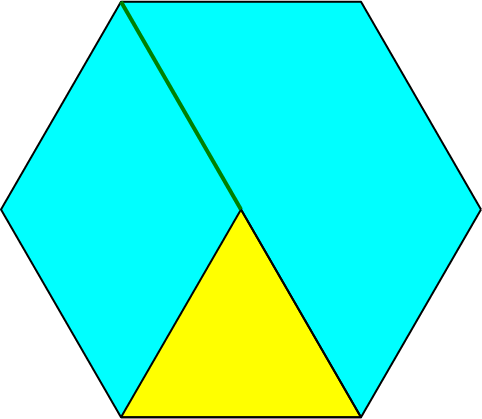
Abb. 1: Dreieck im Sechseck

3 Problemstellung

Für welche Position des Dreiecks sind der grüne und der magenta Diagonalenabschnitt (Abb. 1) gleich lang?

4 Bearbeitung

4.1 Der Goldene Schnitt

Die beiden Diagonalenabschnitte sind genau dann gleich lang, wenn die zweite Ecke des Dreiecks die Sechseckseite im Verhältnis des Goldenen Schnittes teilt (Abb. 2). Nachweis durch Rechnung. In der Abbildung 2 ist die das Teilverhältnis im Goldenen Schnitt durch Major (rot) und Minor (blau) dargestellt. Die beiden Diagonalenabschnitte sind gleich lang wie der Minor.

Abb. 2: Goldener Schnitt

Das Teilverhältnis des Goldenen Schnittes finden wir an verschiedenen Orten (Abb. 3).

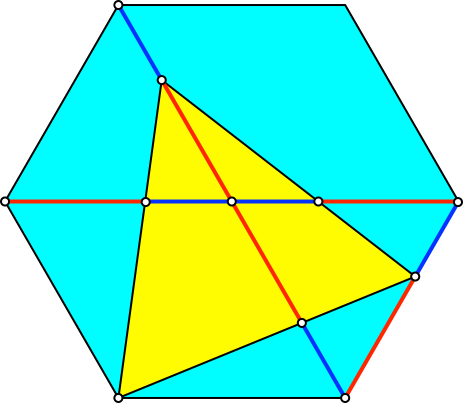
Abb. 3.1: Goldener Schnitt

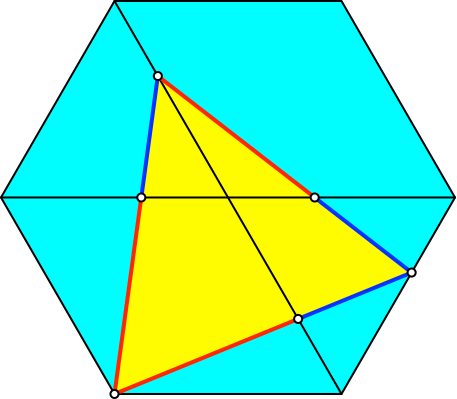
Abb. 3.2: Goldener Schnitt

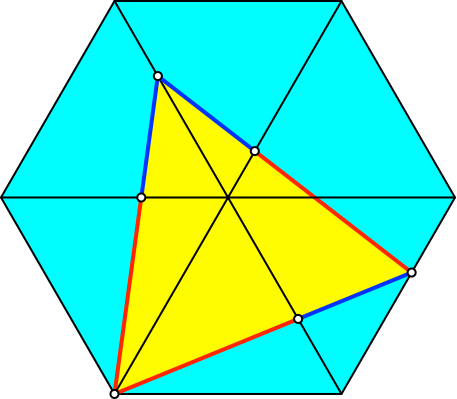
Abb. 3.3: Goldener Schnitt

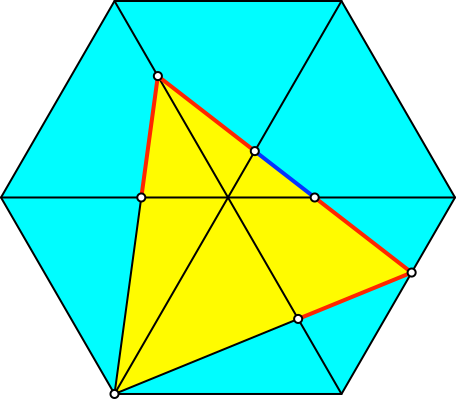
Abb. 3.4: Goldener Schnitt

4.2 Flächenverhältnis

Die Dreiecksfläche ist ein Drittel der Sechsecksfläche. Nachweis rechnerisch: Man zeigt mit dem Kosinus-Satz, dass die Dreiecksseite das √2-fache der Sechsecksseite ist. Damit ist die Dreiecksfläche doppelt so groß wie ein Teildreieck des Sechseckes, das einen Sechstel des Sechseckes ausmacht.

Die Abbildung 4 illustriert den Sachverhalt mit einer gemeinsamen Zerlegung. Jedes Teilstück des Dreiecks kommt im Sechseck dreimal vor.

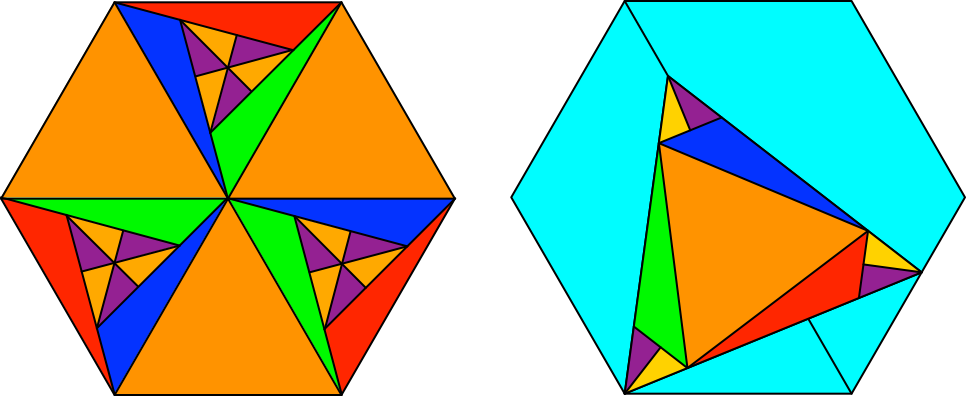
Abb. 4: Gemeinsame Zerlegung

Weblinks

Hans Walser: Dreieck halbieren

https://walser-h-m.ch/hans/Miniaturen/D/Dreieck_halbieren/Dreieck_halbieren.htm