Hans Walser, [20240603]

Eulergerade

1 Worum es geht

Konstruktion eines Punktes, welcher auf der Eulergeraden liegt.

Strahlensätze, Perspektivähnlichkeit

2 Konstruktion

Zu einem Dreieck ABC zeichnen wir die Eulergerade (durch den Schwerpunkt S und den Umkreismittelpunkt M) (Abb. 1). Weiter strecken wir den Punkt A von B aus mit dem Streckfaktor k. In der Abbildung 1 wird k = 0.25 angenommen. Der Bildpunkt sei A‘. Analog konstruieren wir in zyklischer Reihenfolge B‘ und C‘.

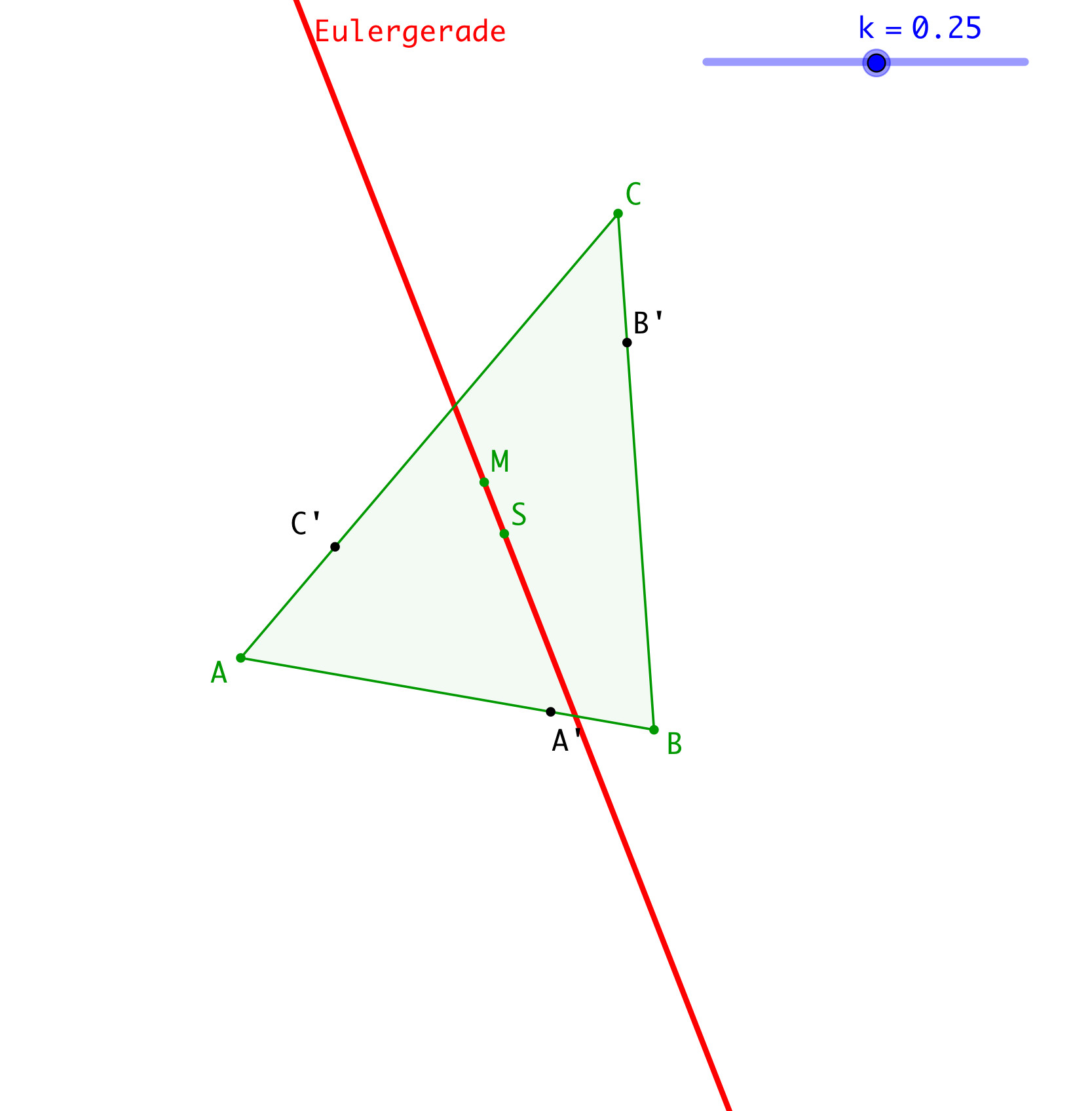
Abb. 1: Start

Nun strecken wir den Punkt A von C aus mit demselben Streckfaktor k (Abb. 2). Der Bildpunkt sei A‘₁. Analog B‘₁ und C‘₁.

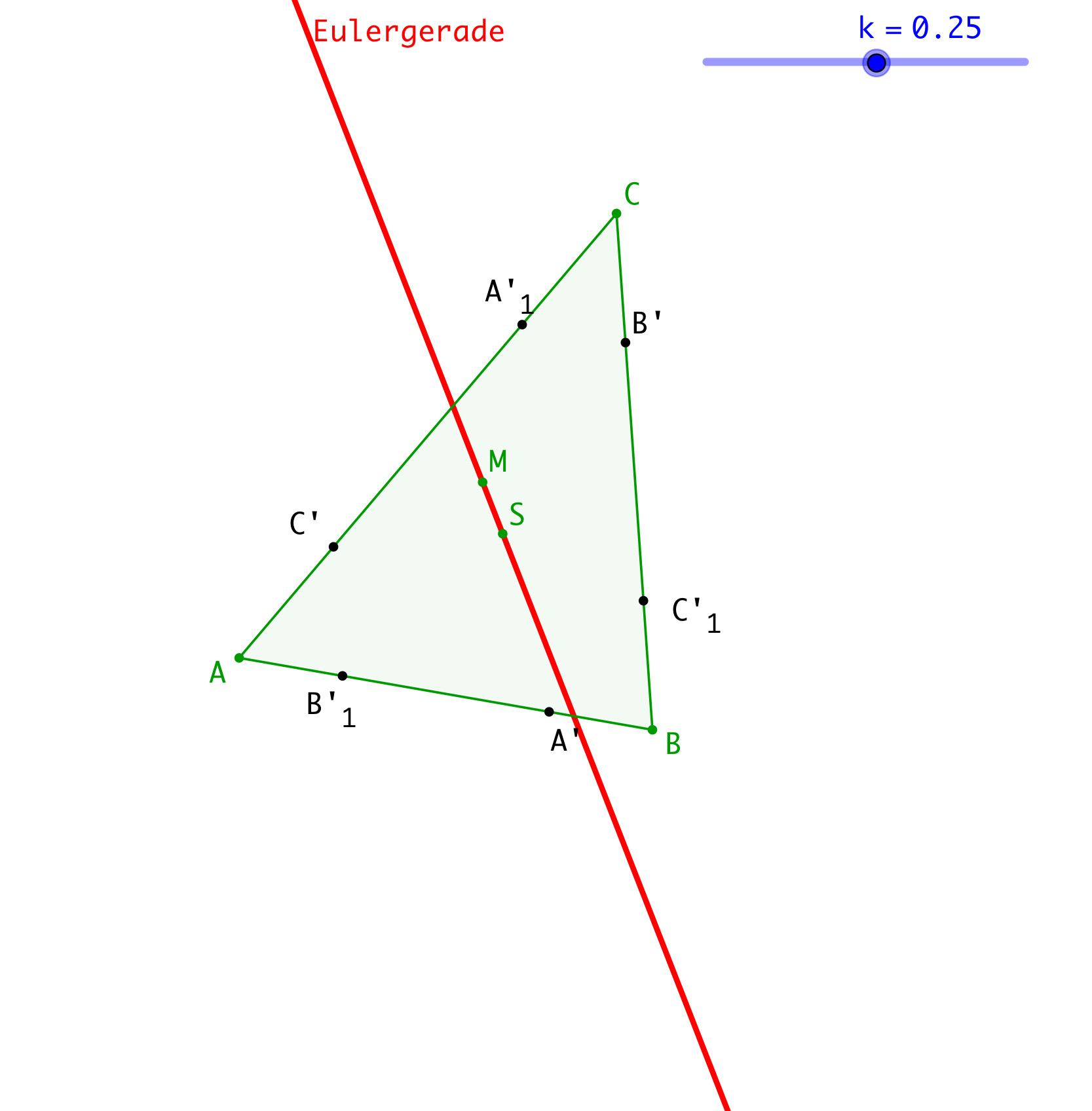
Abb. 2: Weitere Streckungen

Wir zeichnen nun das Dreieck DEF gemäß Abbildung 3.

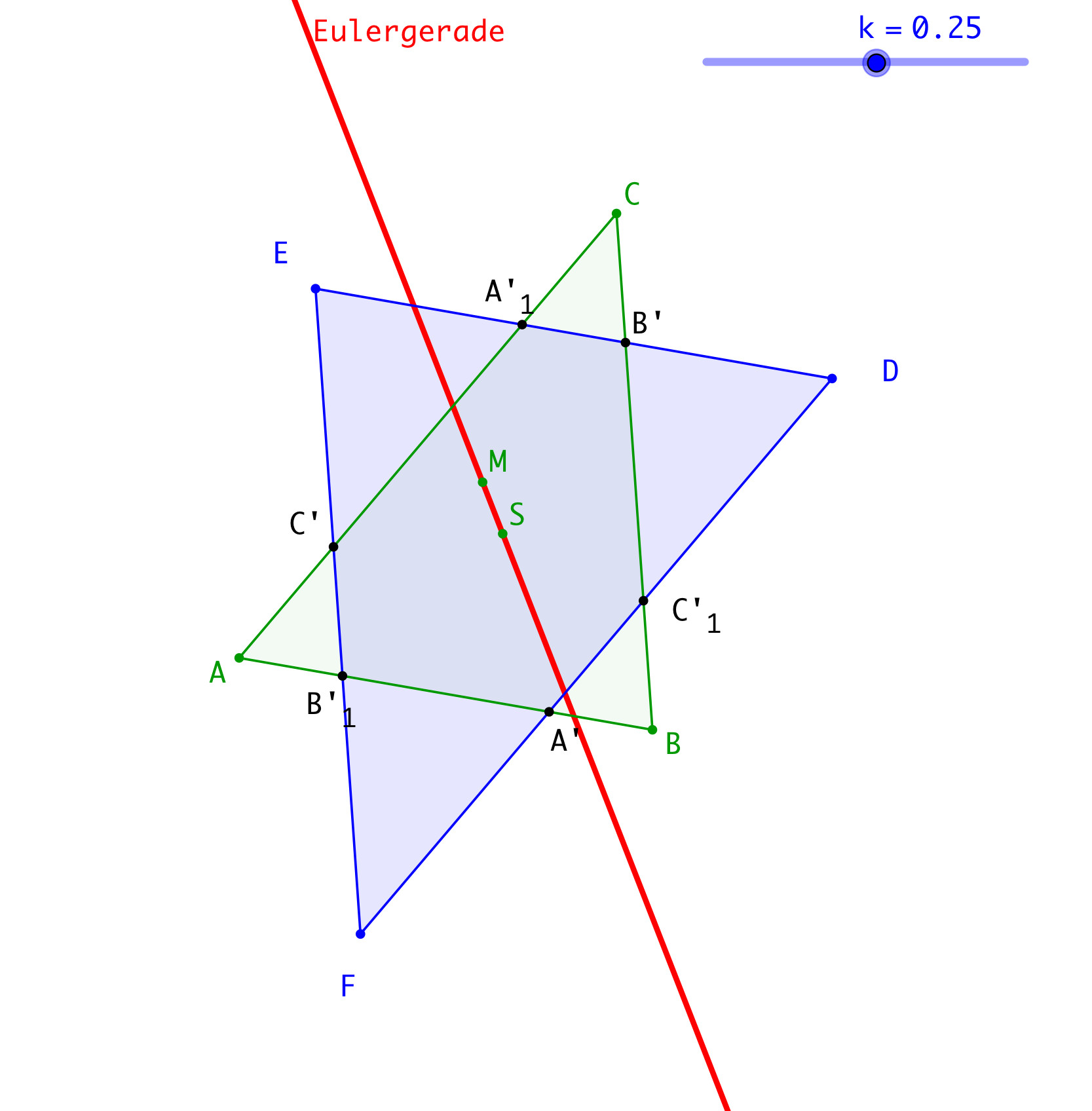
Abb. 3: Dreieck DEF

Der Mittelpunkt P des Umkreises des Dreiecks DEF liegt auf der Eulergeraden des Dreiecks ABC (Abb. 4 und 5).

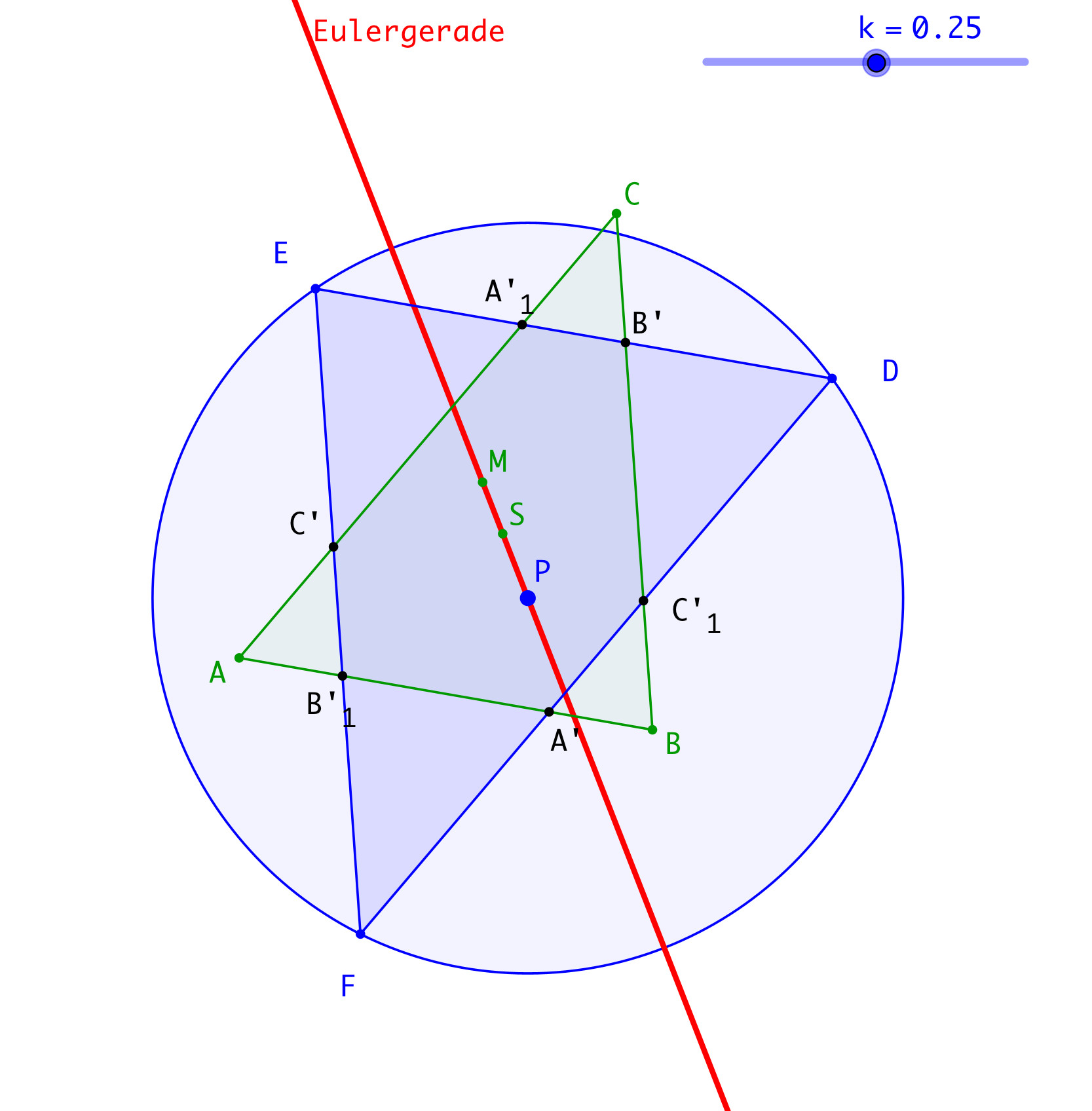
Abb. 4: Mittelpunkt auf Eulergeraden

Die Abbildung 5 zeigt eine Animation mit Variation des Streckfaktors k.

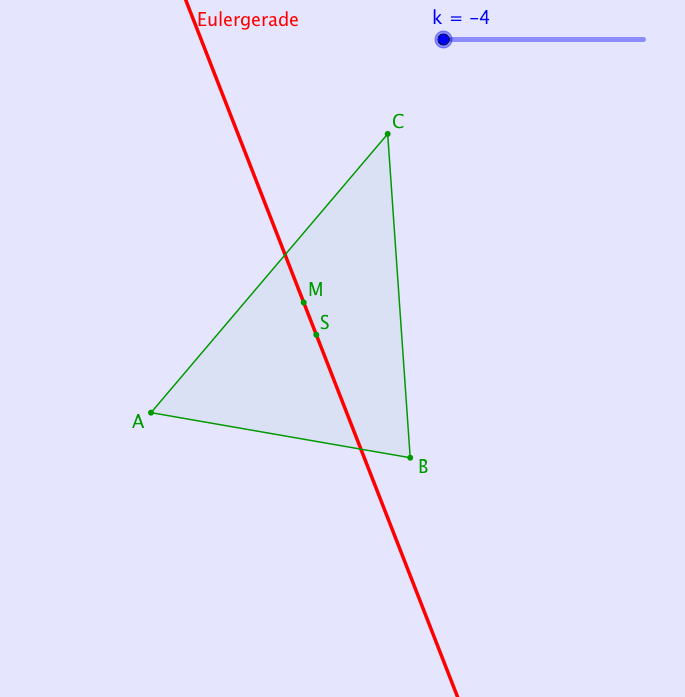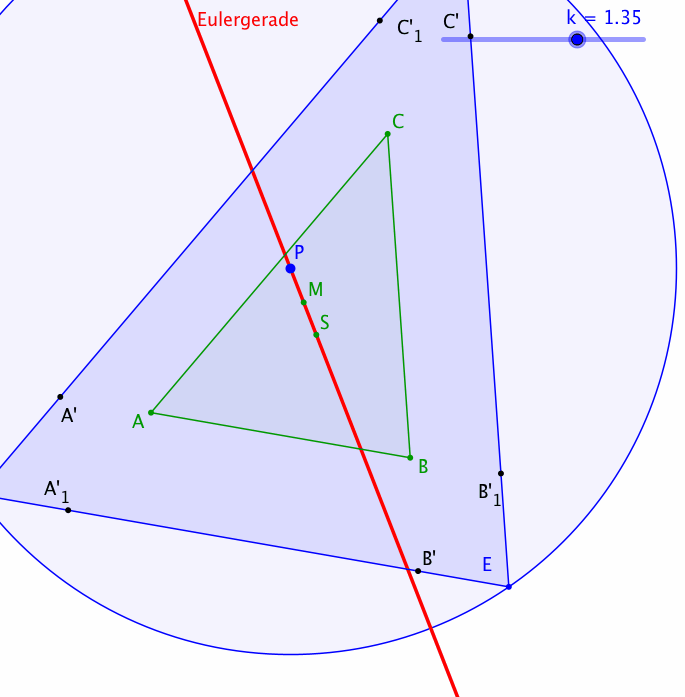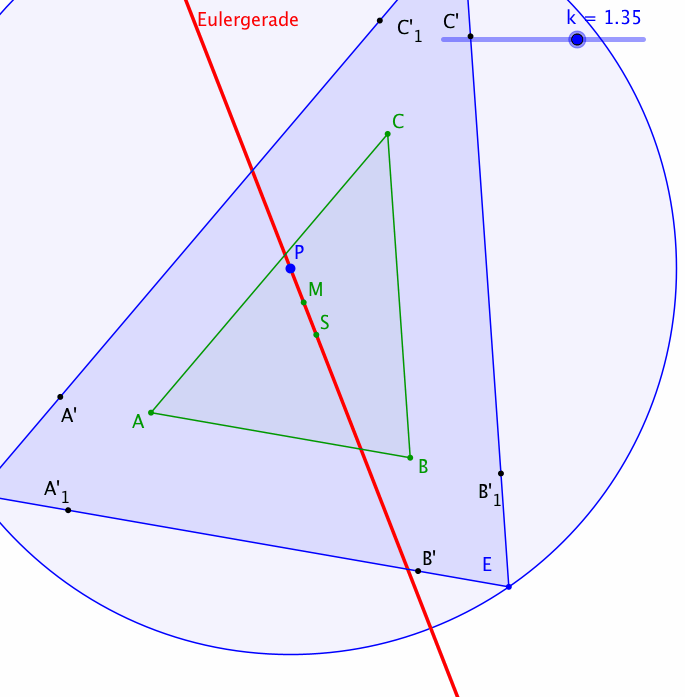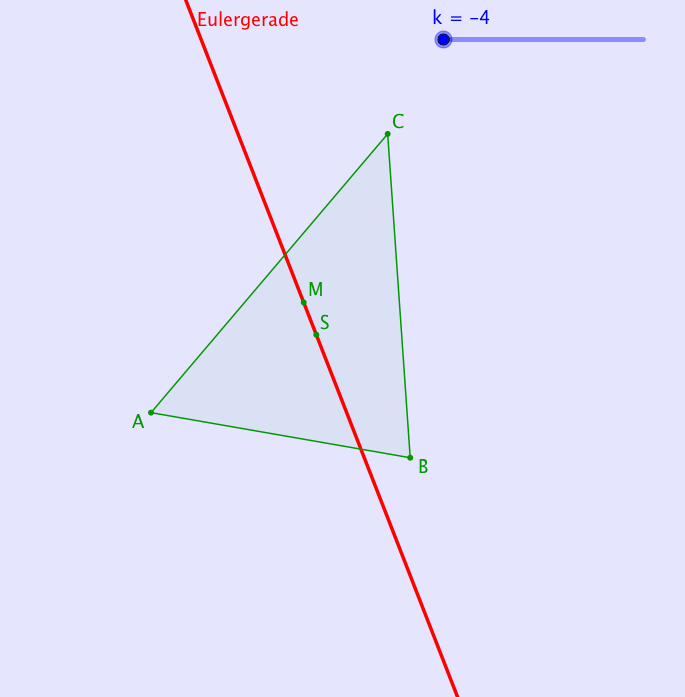
Abb. 5: Animation

3 Sonderfälle

Für k = ⅓ sind die beiden Dreiecke ABC und DEF kongruent (Abb. 6). Sie liegen punktsymmetrisch gegenüber dem Schwerpunkt S des Dreiecks ABC. Somit ist S auch der Schwerpunkt des Dreiecks DEF. Der Punkt P ist der Spiegelpunkt von M bei Spiegelung an S.

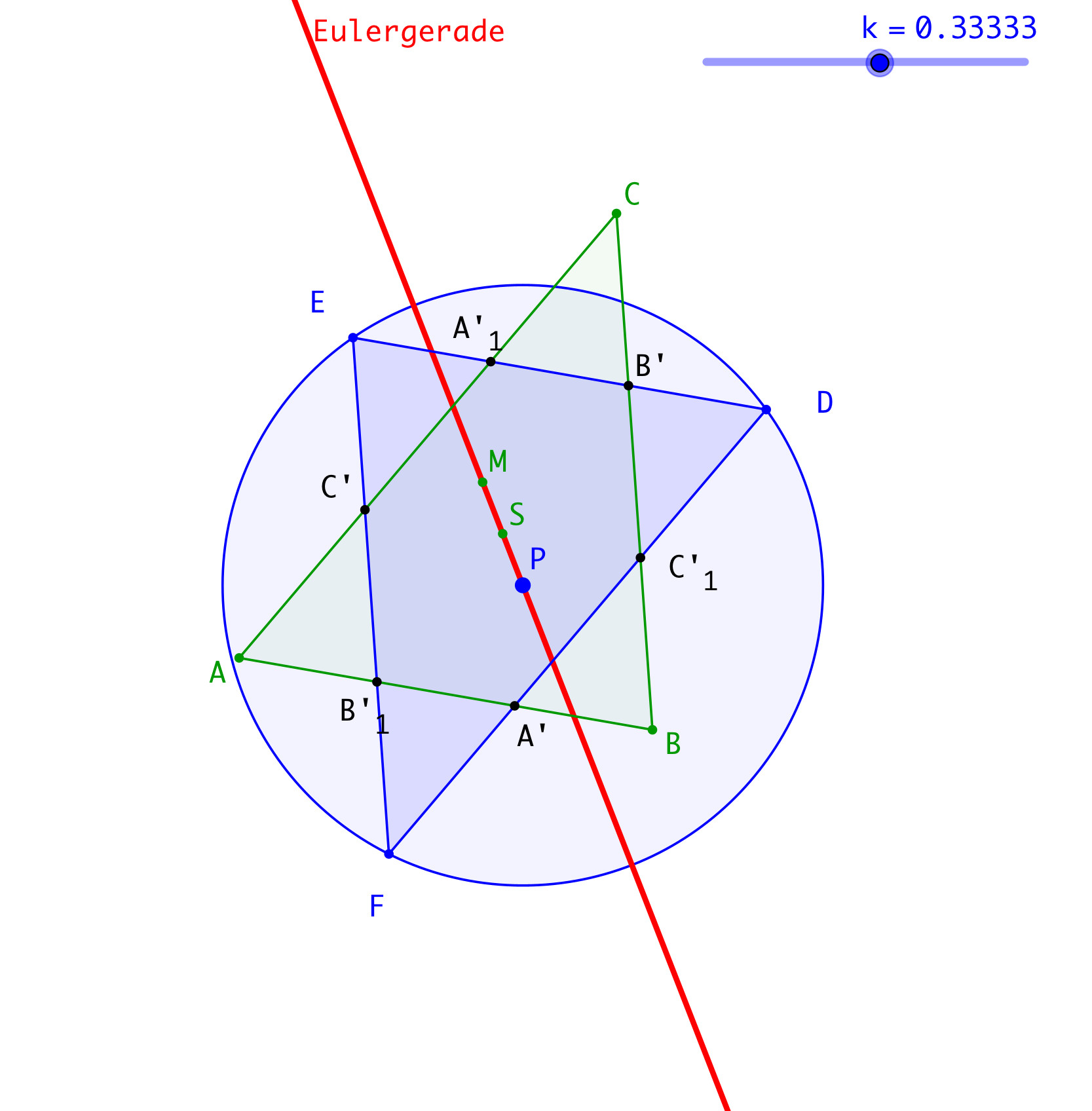
Abb. 6: Punktsymmetrische Dreiecke

Für k = ½ ist das Dreieck DEF das Kantenmittendreieck von ABC (Abb. 7). Der Umkreis des Dreiecks DEF ist der Feuerbachkreis des Dreiecks ABC. Das Zentrum des Feuerbachkreises liegt auf der Eulergeraden.

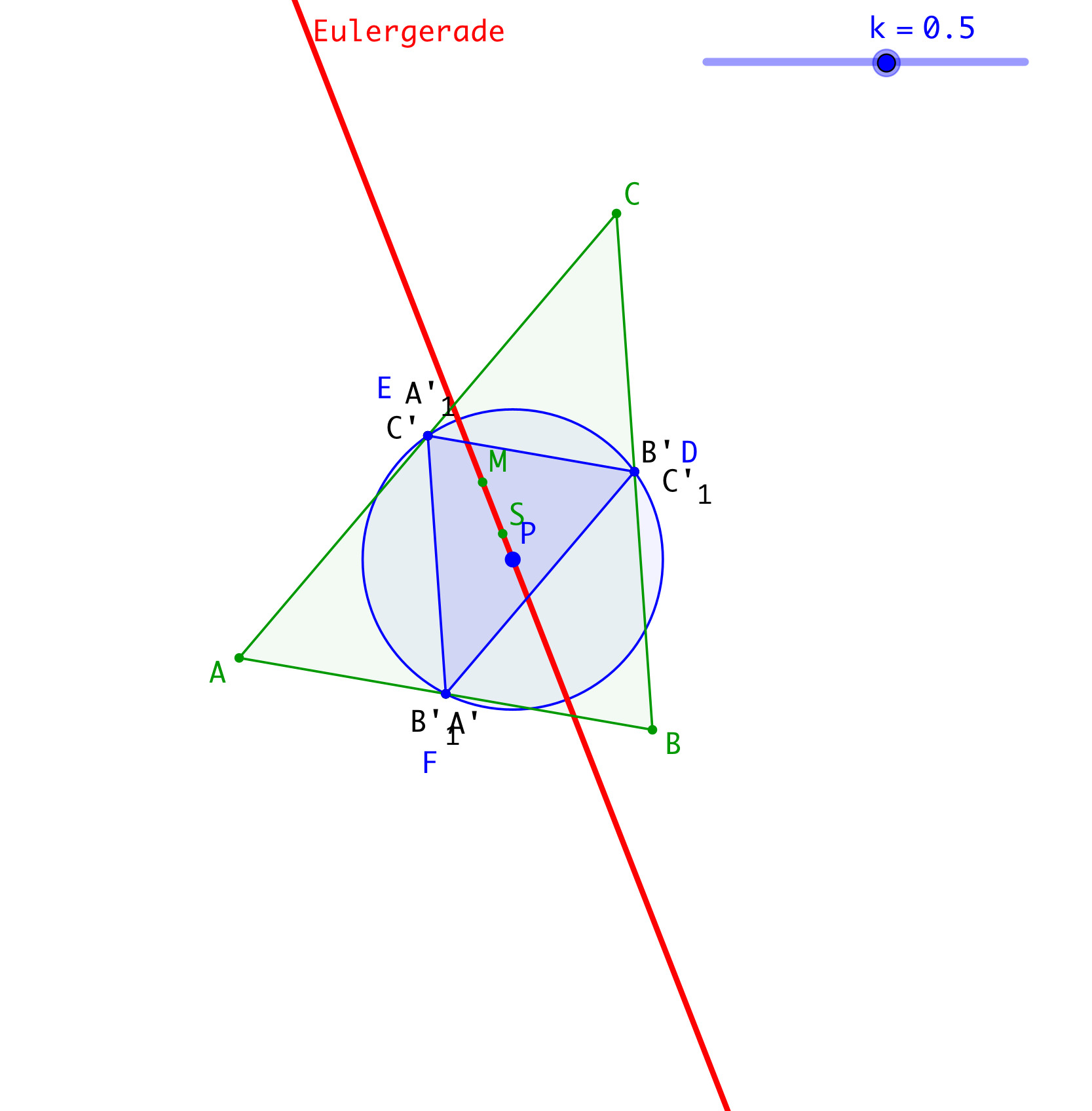
Abb. 7: Feuerbachkreis

Für k = 1 fallen die beiden Dreiecke DEF und ABC aufeinander (Abb. 8). P fällt auf M.

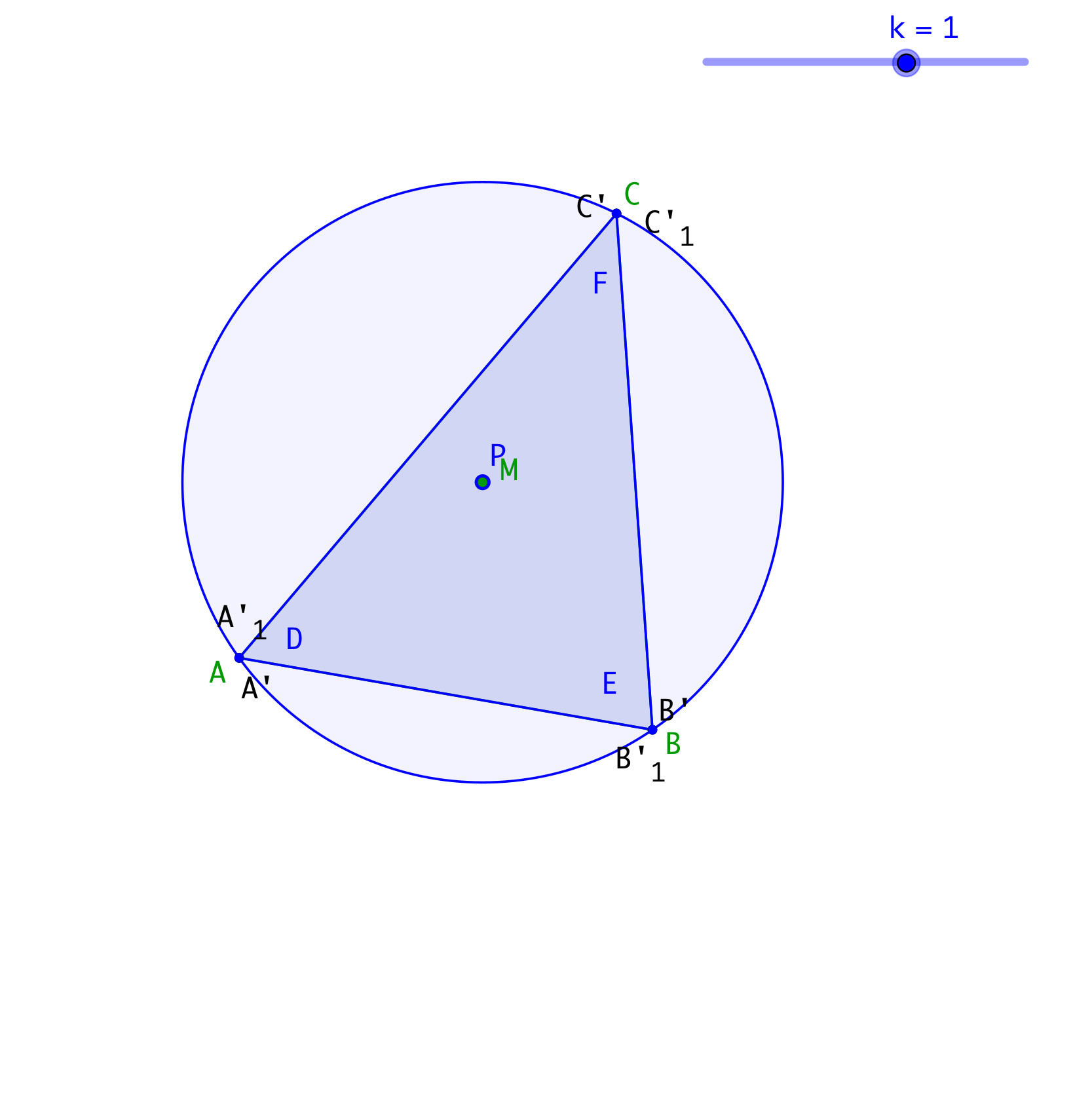
Abb. 8: Kongruente Dreiecke

In allen drei Sonderfällen geht das Dreieck DEF durch eine Streckung an S mit dem Streckfaktor s aus dem Dreieck ABC hervor. Die Tabelle 1 zeigt den Zusammenhang zwischen k und s.

Streckfaktor k	⅓	½	1
Streckfaktor s	–1	–½	1

Tab. 1: Die beiden Streckfaktoren

4 Beweis

Auf Grund der Strahlensätze geht das Dreieck DEF allgemein aus dem Dreieck ABC durch eine Streckung an S hervor. Der Zusammenhang zwischen k und s ist linear. Aus der Tabelle 1 ergibt sich:

s = 3k – 2

Damit ist P des Bild von M bei dieser Streckung. Da S und M beide auf der Eulergeraden liegen, gilt dies auch für P.

Weblinks

Hans Walser: Eulergerade

https://walser-h-m.ch/hans/Miniaturen/E/Eulergerade4/Eulergerade4.html

Hans Walser: Euler-Gerade

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade/Eulergerade.htm

Hans Walser: Eulergerade

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade2/Eulergerade2.htm

Hans Walser: Ein merkwürdiger Punkt auf der Eulergeraden

http://www.walser-h-m.ch/hans/Miniaturen/E/Eulergerade3/Eulergerade3.htm

Hans Walser: Kiepert-Gerade

http://www.walser-h-m.ch/hans/Miniaturen/K/Kiepert-Gerade/Kiepert-Gerade.html