Hans Walser, [20241004]

Flächengleiche Rechtecke

Anregung: Wilfried Dutkowsi, Bonn

1 Problemstellung

Zu einem Quadrat ist ein flächengleiches Rechteck gesucht, dessen obere rechte Ecke auf der verlängerten Quadratdiagonalen liegt (Abb. 1).

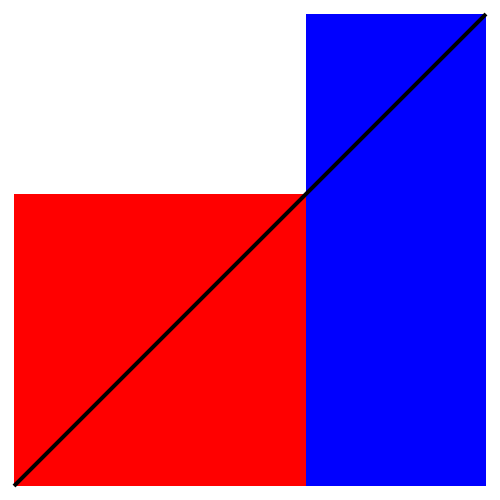
Abb. 1: Quadrat und flächengleiches Rechteck

2 Bearbeitung

Das Quadrat habe die Seitenlänge 1 und damit auch den Flächeninhalt 1.

Weiter sei h die Höhe des Rechteckes. Damit hat das Rechteck die Breite h – 1.

Die Flächenbedingung ergibt:

(h – 1) h = 1

Daraus erhalten wir die quadratische Gleichung

h² – h – 1= 0

mit der positiven Lösung h = (1 + √5)/2 ≈ 1.618. Dies ist der Goldene Schnitt. Die Breite ist h – 1 = (–1 + √5)/2 ≈ 0.618.

Das Rechteck ist ein sogenanntes Hochgoldenes Rechteck.

3 Erweiterung

Wir suchen eine Folge von flächengleichen Rechtecken gemäß Abbildung 2.

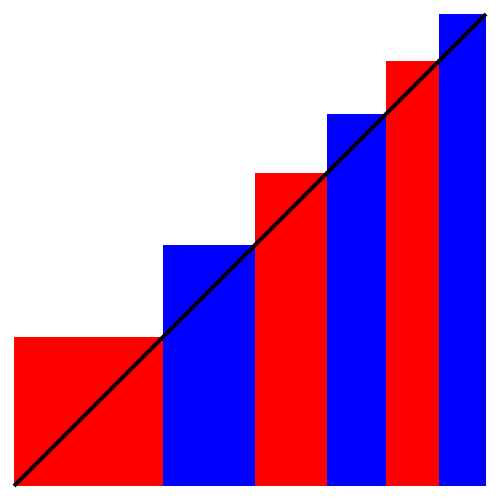
Abb. 2: Folge von flächengleichen Rechtecken

4 Bearbeitung

Wir setzen:

h₀ = 0 (technischer Startwert)

h₁ = 1 (Seitenlänge des Startquadrates)

Weiter sei h₂ die Höhe des anschließenden Rechteckes, h₃ die Höhe des daran anschließenden Rechteckes und so weiter.

Aus der Flächenbedingung

(h_n – h_n–1) h_n = 1

ergibt sich die Rekursion:

h_n = ½ (h_n–1 + √( h_n–1² + 4))

Die Tabelle 1 zeigt die ersten Werte.

n	hn	hn – hn–1
1	1	1	Startquadrat
2	1.618033988	0.618033988	Hochgoldenes Rechteck
3	2.095293984	0.477259996
4	2.495943998	0.400650014
5	2.847169957	0.351225959
6	3.163295928	0.316125971

Tab. 1: Rechteckhöhen

Weblinks

Hans Walser: Hochgoldenes Rechteck

https://walser-h-m.ch/hans/Miniaturen/H/Hochgoldenes_Rechteck/Hochgoldenes_Rechteck.html

Hans Walser: Hochgoldenes Rechteck

https://walser-h-m.ch/hans/Miniaturen/H/Hochgoldenes_Rechteck2/Hochgoldenes_Rechteck2.html

Literatur

Walser, Hans (2024): Der Goldene Schnitt. Geometrische und zahlentheoretische Betrachtungen. 7. Auflage. Springer Spektrum.
Print-ISBN 978-3-662-68556-3. E-Book_ISBN 978-3-662-68557-0.
https://doi.org/10.1007/978-3-662-68557-0