Hans Walser, [20240311], [20240421]
Flächengleichheit
Idee und Anregungen:
Hartmut Müller-Sommer, Vechta
1 Worum es geht
Ein Flächensatz im rechtwinkligen Dreieck.
Möndchen des Hippokrates.
Zerlegungsgleichheit.
2 Konstruktion
In einem beliebigen rechtwinkligen Dreieck zeichnen wir den Inkreis (Abb. 1).
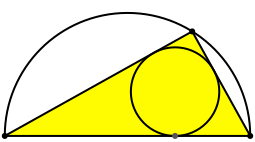
Abb. 1: Inkreis im rechtwinkligen Dreieck
Der Berührungspunkt des Inkreises mit der Hypotenuse teilt diese in zwei Abschnitte. Wir zeichnen das Rechteck aus diesen beiden Hypotenusenabschnitten (Abb. 2).
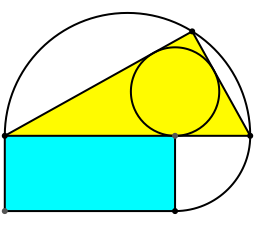
Abb. 2: Rechteck aus den Hypotenusenabschnitten
3 Flächengleichheit
Das gelbe Dreieck und das blaue Rechteck haben denselben Flächeninhalt (Abb. 3).
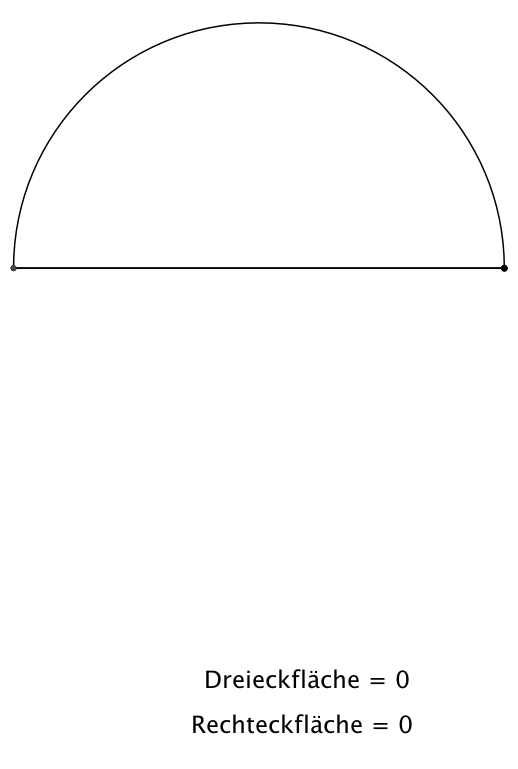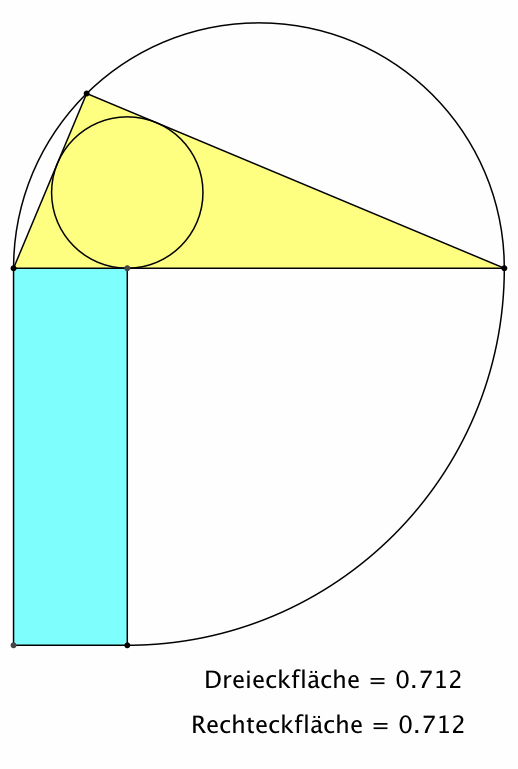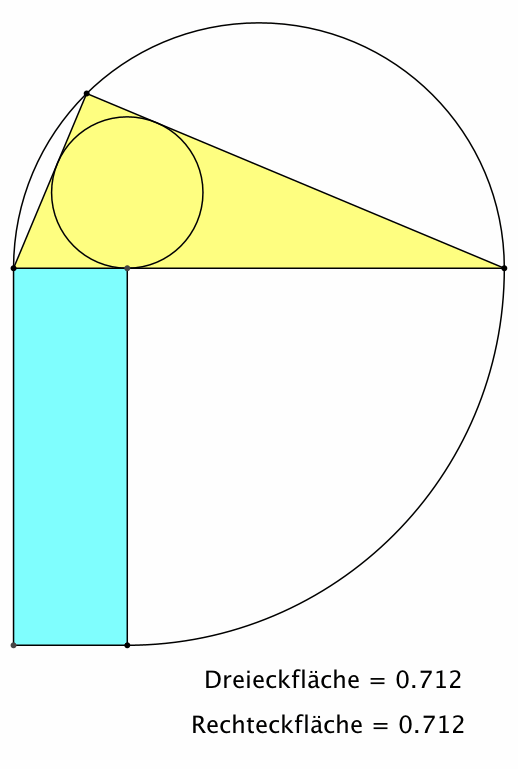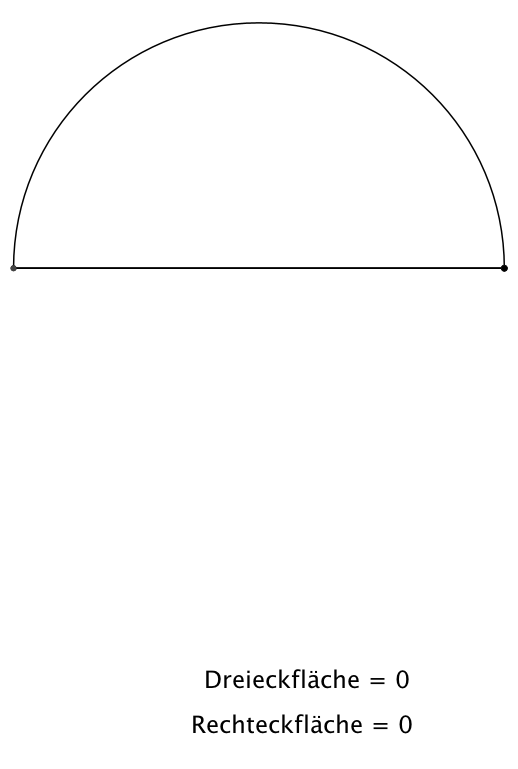
Abb. 3: Flächengleichheit
4 Rechnerischer Beweis
Wir bezeichnen die Katheten mi a und b. Für die Hypotenuse c gilt nach dem Satz des Pythagoras c = √(a2+ b2). Weiter sei s der halbe Umfang des Dreieckes, also s = ½(a + b +c). Die beiden Hypotenusenabschnitte haben die Länge (s – a) und (s – b). Dies ergibt sich aus der Theorie des Inkreises im Dreieck.
Für den Flächeninhalt des blauen Rechteckes erhalten wir somit:
Flächeninhalt des
blauen Rechteckes = (s – a)(s – b)
= s2 – sa – sb + ab
= ¼(a2 + b2
+ c2 + 2ab + 2ac + 2bc) – ½(a2
+ ab + ac) – ½(ab + b2
+ bc) + ab
= ¼(a2 + b2
+ a2 + b2 + 2ab + 2ac + 2bc)
– ½(a2 + ab + ac) –
½(ab + b2 + bc) + ab
= ¼(2a2 + 2b2
+ 2ab + 2ac + 2bc) – ½(a2 + ab + ac) – ½(ab + b2 + bc) + ab
= ½(a2 + b2
+ ab + ac + bc)
– ½(a2 + ab + ac) –
½(ab + b2 + bc) + ab
= ½ab
Das gelbe
rechtwinklige Dreieck hat ebenfalls den Flächeninhalt ½ab. Damit ist die
Flächengleichheit gezeigt.
5
Anhängen
des Höhensatzes
Mit dem Höhensatz
können wir das blaue Rechteck in ein flächengleiches Quadrat umformen. Damit
haben wir eine Konstruktion, welche die Dreiecksfläche direkt in eine
Quadratfläche umformt (Abb. 4).
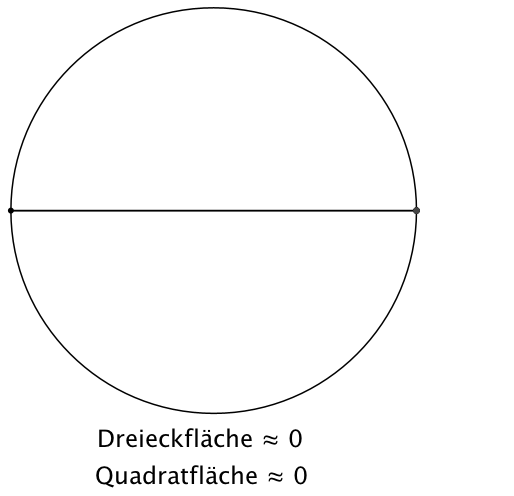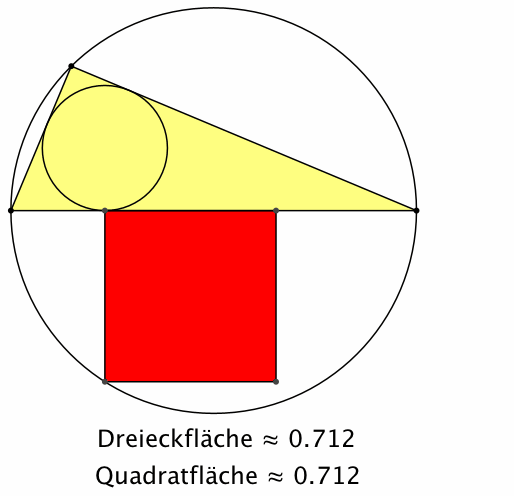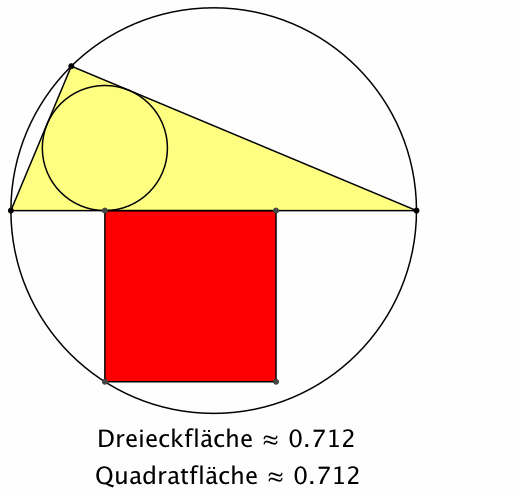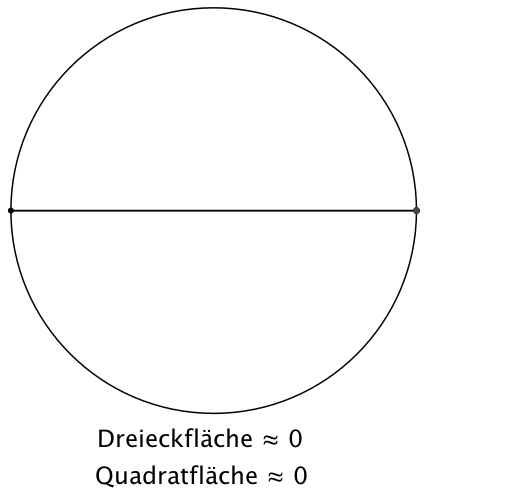
Abb. 4: Vom
Dreieck zum Quadrat
6
Andere
Anordnung
Die Hypotenusenabschnitte
erscheinen auch auf den Katheten als gleich lange Tangentenabschnitte an den
Inkreis. Daher können wir das blaue Rechteck anders anordnen (Abb. 5). Der
Inkreismittelpunkt ist jetzt eine Ecke des Rechteckes.
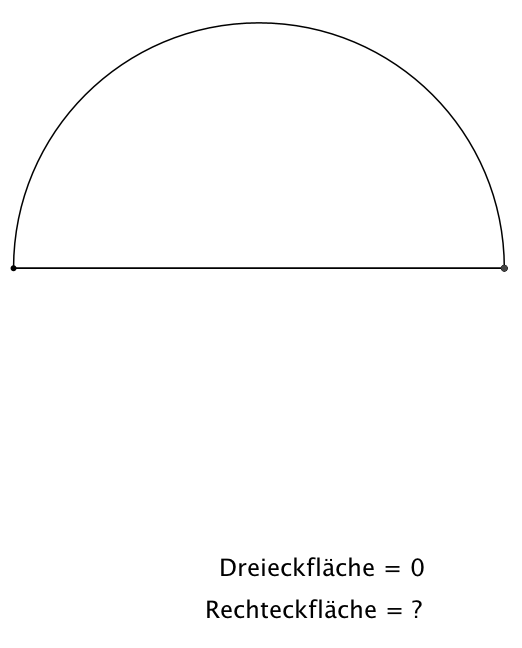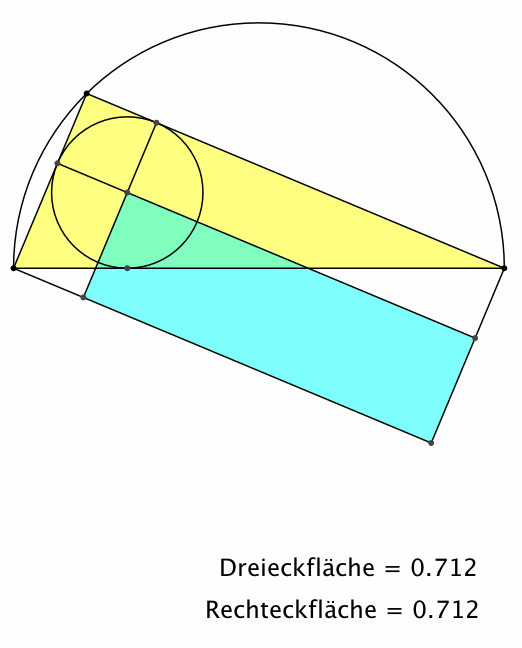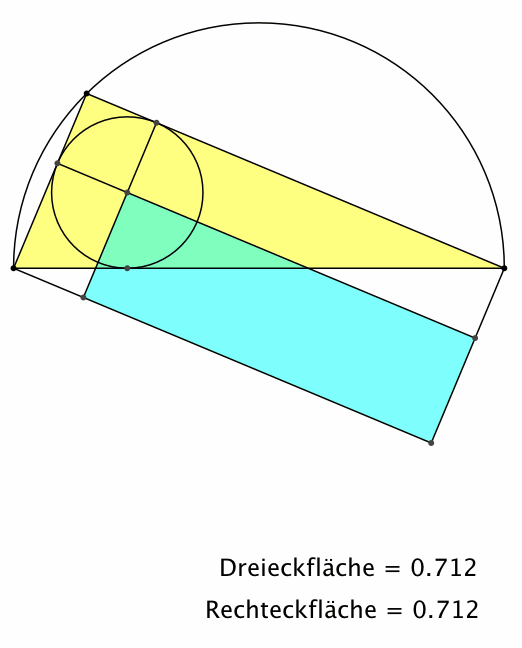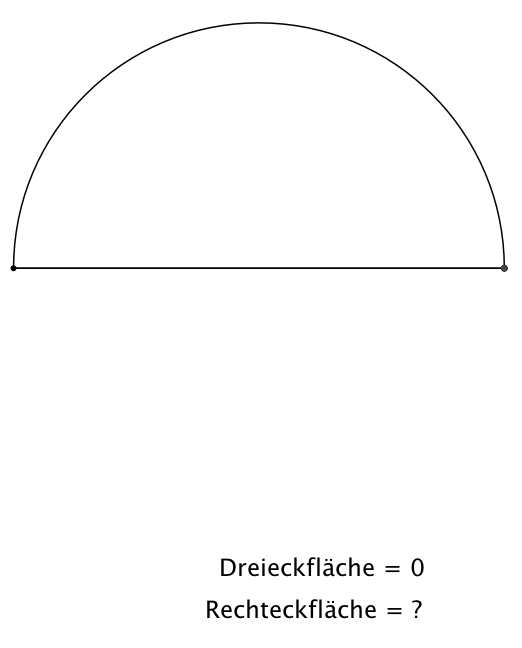
Abb. 5: Andere Anordnung
Die Abbildung 6 gibt
einen Hinweis auf die Zerlegungsgleichheit.
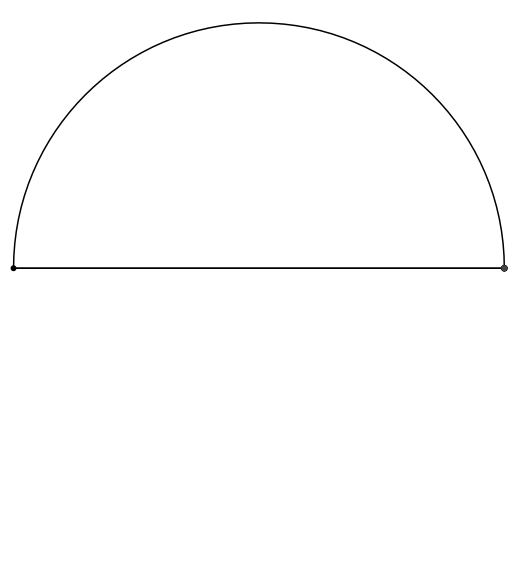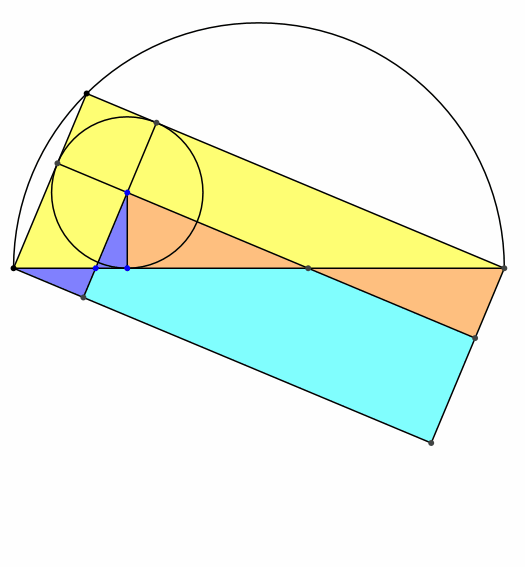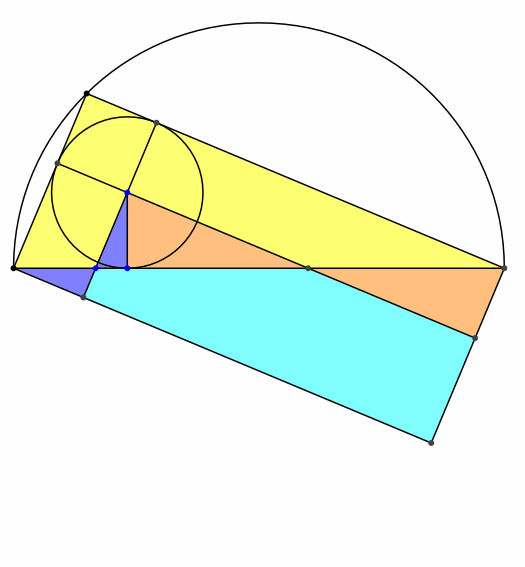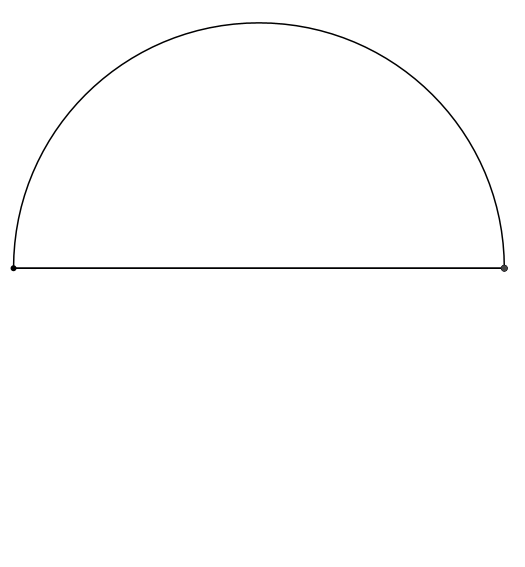
Abb. 6:
Zerlegung
7
Möndchen
des Hippokrates
Auch die sind immer
wieder lustig (Abb. 7).
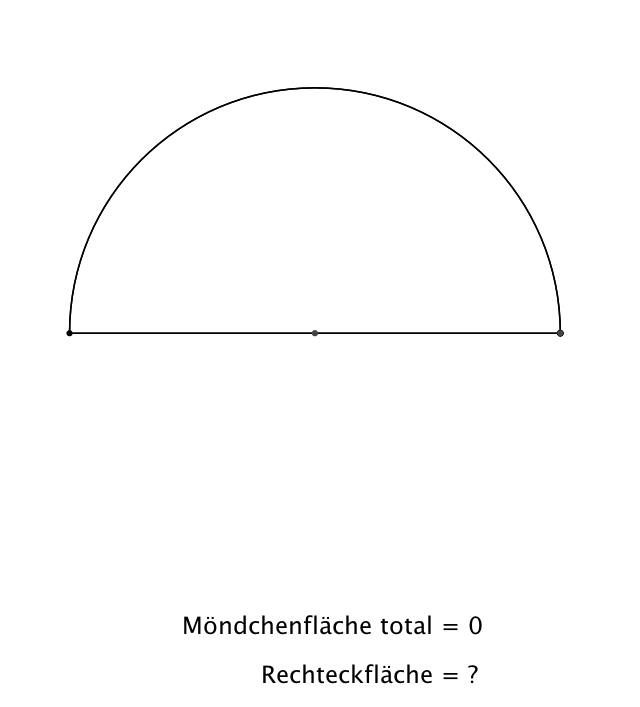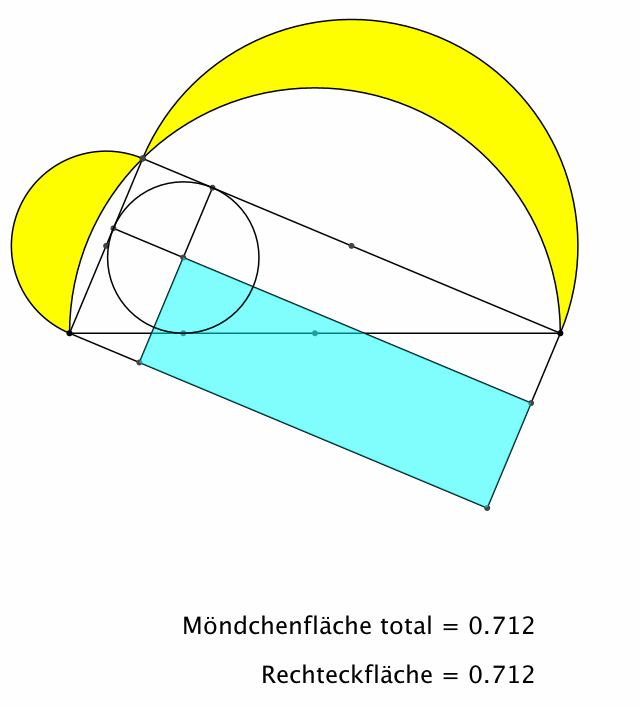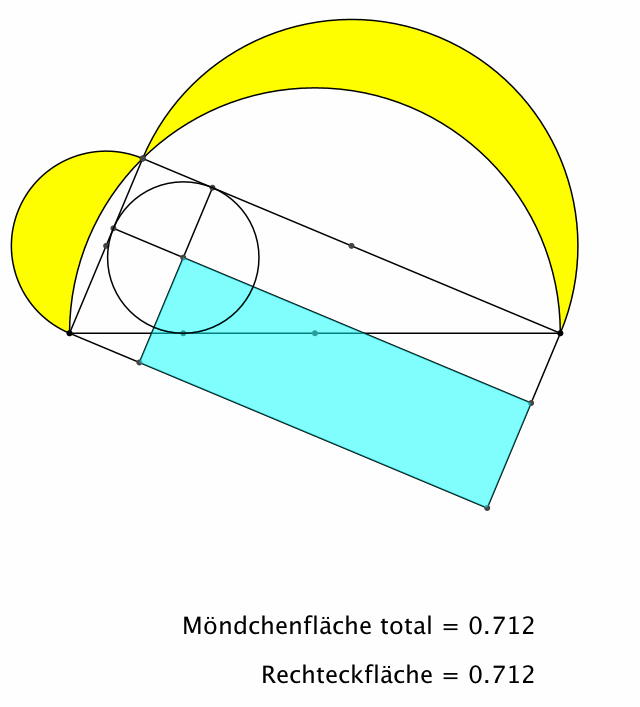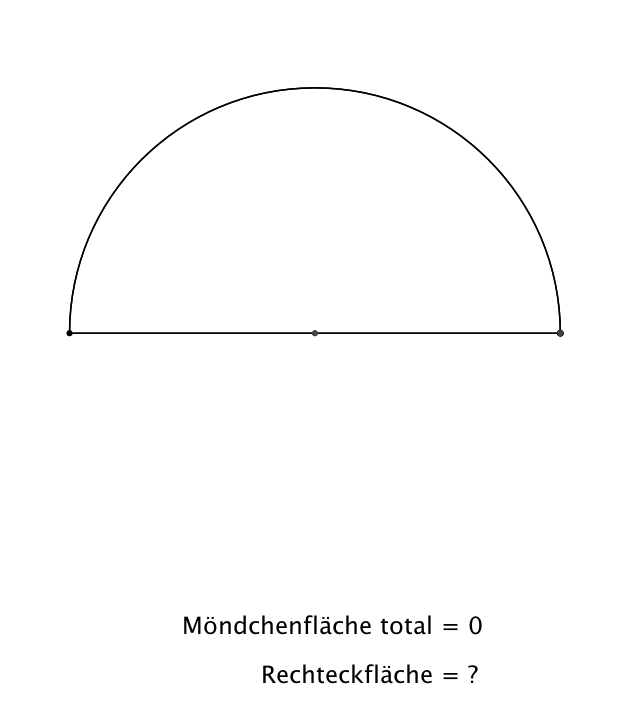
Abb. 7:
Möndchen des Hippokrates
8
Zerlegungsgleichheit
Für die Illustration
der Zerlegungsgleichheit verwenden wir eine Gegenüberstellung in einer anderen
Anordnung (Abb. 8).

Abb. 8: Andere
Anordnung
Damit ergibt sich
eine gemeinsame Zerlegung (Abb. 9).

Abb. 9:
Gemeinsame Zerlegung
In der Überlagerung
der beiden Figuren der Abbildung 9 erscheinen zwei Schmetterlinge (Abb. 10). Die
Symmetrieachsen der beiden Schmetterlinge schneiden sich auf dem Umkreis.
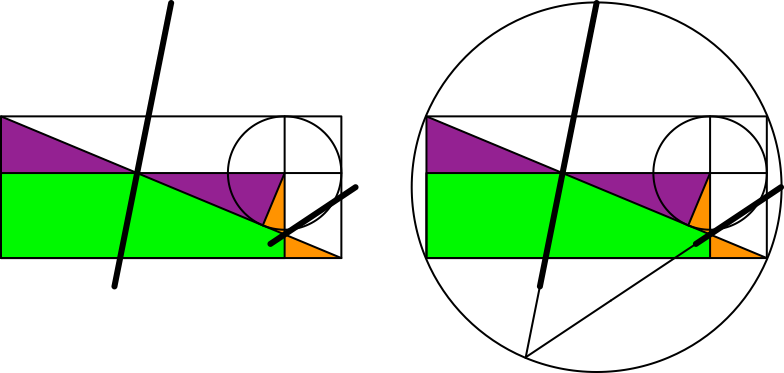
Abb. 10:
Schmetterlinge
Links
Thomas Jahre: Aufgabe der Woche
https://www.schulmodell.eu/aufgabe-der-woche.html
Hans Walser: Flächengleichheit
https://walser-h-m.ch/hans/Miniaturen/F/Flaechengleichheit4/Flaechengleichheit4.html
Hans Walser: Inkreis und Umkreis
https://walser-h-m.ch/hans/Miniaturen/I/Inkreis_und_Umkreis/Inkreis_und_Umkreis.html