Hans Walser, [20231129]
Goldener Schnitt
Idee und Anregung: Maik Rentsch, Dresden
1 Worum es geht
Goldener Schnitt bei einer speziellen Parabel vierten Grades.
2 Zwei Parabeln
Wir schneiden die Parabel vierten Grades y = x(x – 1)(x – 2)(x – 3) (rot in Abb. 1) mit der quadratischen Parabel y = (x – 1)(x – 2) (blau in Abb. 1).
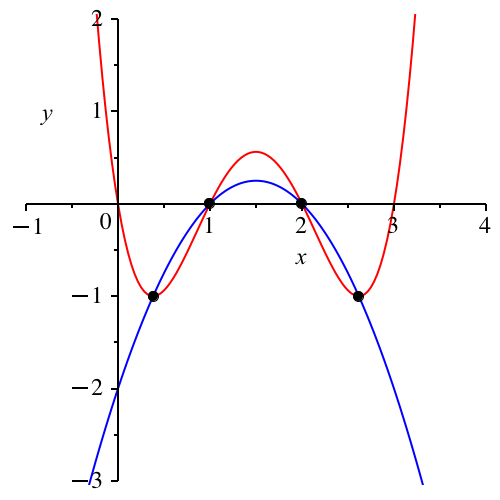
Abb. 1: Parabel vierten und Parabel zweiten Grades
3 Schnittpunkte
Zur Beschreibung der Schnittpunkte verwenden wir den Goldenen Schnitt Φ = (1 + √5)/2 ≈ 1.618.
Die vier Schnittpunkte der beiden Parabeln haben von links nach rechts die Koordinaten:
((1/ Φ)2, –1), (1, 0), (2, 0), (Φ2, –1)
Die beiden Schnittpunkte mit den Koordinaten ((1/ Φ)2, –1) und (Φ2, –1) sind zudem die Minimalpunkte der roten Parabel. Der horizontale Abstand dieser beiden Punkte ist √5 ≈ 2.236.
4 Flächeninhalte
Die Bereiche zwischen den beiden Kurven haben von links nach rechts die Flächeninhalte –1/10, 1/5, –1/10. Ihre Beträge verhalten sich also wie 1 : 2 : 1.
Das Goldene Trapez (Abb. 2) hat den Flächeninhalt Φ.
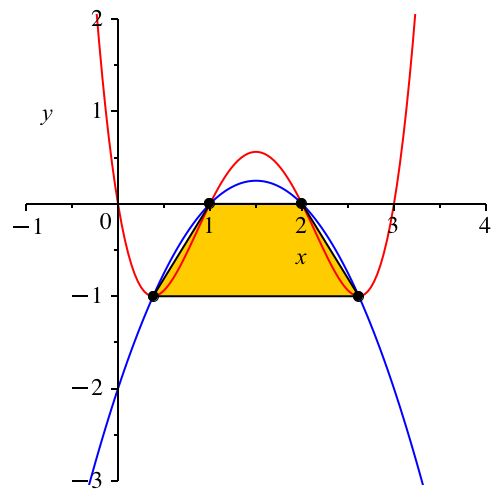
Abb. 2: Goldenes Trapez
Weblink
Hans Walser: Parabel vierten Grades
https://walser-h-m.ch/hans/Miniaturen/P/Parabel_4-ten_Grades/Parabel_4-ten_Grades.htm