1 Worum es geht

Konstruktion des Goldenen Schnittes mit einem Inkreis

2 Problemstellung

Eine gegebene Strecke (Abb. 1a) soll im Verhältnis des Goldenen Schnittes geteilt werden.

3 Konstruktionsgang

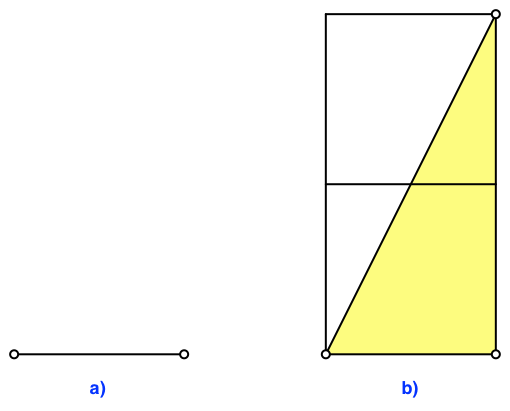
Abb. 1: Strecke. Dreieck

Wir konstruieren ein rechtwinkliges Dreieck mit der gegebenen Strecke als kurzer Kathete. Die lange Kathete soll doppelt so lang sein (Abb. 1b).

In dieses Dreieck zeichnen wir den Inkreis (Abb. 2a).

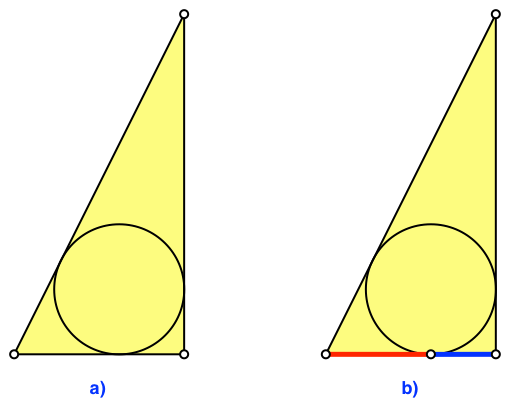
Abb. 2: Inkreis. Goldener Schnitt

Der Berührungspunkt des Inkreises mit der gegebenen Strecke unterteilt diese im Verhältnis des Goldenen Schnittes (Abb. 2b).

4 Rechnerischer Nachweis

Mit Φ = (1 + √5)/2 ≈ 1.618 bezeichnen wir den Goldenen Schnitt.

Die gegebene Strecke habe die Länge 1.

In der üblichen Bezeichnung für das rechtwinklige Dreieck gilt nun:

a = 1, b = 2, c = √5 ≈ 2.236

Der Inkreisradius ρ eines rechtwinkligen Dreiecks hat die Länge:

ρ = ½(a + b – c)

In unserem Fall heißt dies:

ρ = ½(3 – √5) = (1/ Φ)² ≈ 0.382

Dies ist die Länge des blauen Abschnittes in der Abbildung 2b (Minor). Für den roten Abschnitt (Major) erhalten wir 1 – (1/ Φ)² = 1/ Φ ≈ 0.618.

Für das Teilverhältnis ergibt sich:

Major:Minor = Φ:1

Dies war zu zeigen.

Weblinks

Hans Walser: Goldener Schnitt im Doppelquadrat

https://walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_im_Doppelquadrat/Goldener_Schnitt_im_Doppelquadrat.html

Hans Walser: Miniaturen: Goldener Schnitt

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html

Literatur

Walser, Hans (2024): Der Goldene Schnitt. Geometrische und zahlentheoretische Betrachtungen. 7. Auflage. Springer Spektrum.
Print-ISBN 978-3-662-68556-3. E-Book_ISBN 978-3-662-68557-0.
https://doi.org/10.1007/978-3-662-68557-0