Hans Walser, [20240822]

Konvexe Hülle

Anregung: Wilfried Dutkowski, Bonn

1 Worum es geht

Konvexe Hülle von Figuren, die aus einem Würfel und einem Oktaeder bestehen

2 Konstruktion

Einem Würfel beschreiben wir ein Oktaeder ein, dessen Ecken die Seitenmitten des Würfels sind (Abb. 1).

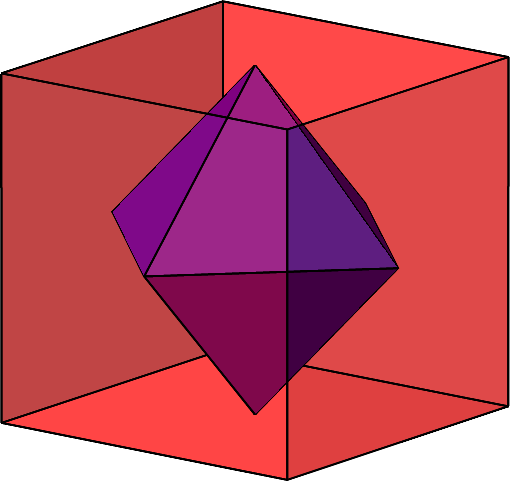
Abb. 1: Oktaeder im Würfel

Nun verkleinern wir den Würfel und vergrößern gleichzeitig das Oktaeder, bis wir die umgekehrte Situation haben: dem Oktaeder ist der Würfel so einbeschrieben, dass die Würfelecken die Seitenmitten des Oktaeders sind (Abb. 2).

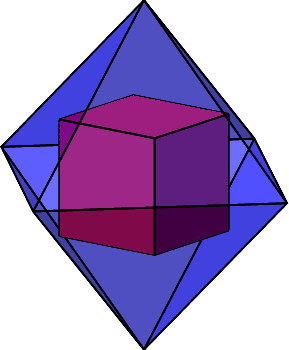
Abb. 2: Würfel im Oktaeder

Die Abbildungen 3 und 4 illustrieren diesen Prozess.

Abb. 3: Transformation

Abb. 4: Transformation

3 Sonderfall

In der Mitte halbieren sich die Würfelkanten und die Oktaederkanten gegenseitig (Abb. 5). Zudem sind sie orthogonal.

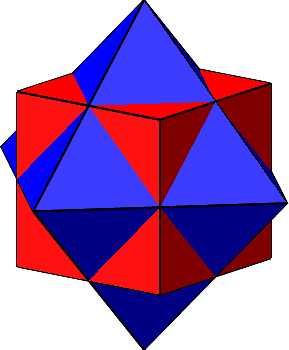
Abb. 5: Sonderfall

4 Konvexe Hülle

Nun zeichnen wir die konvexe Hülle (Abb. 6) zu den Figuren der Abbildungen 3 und 4.

Abb. 6: Konvexe Hülle

Zu Beginn ist die konvexe Hülle der Startwürfel.

Im Sonderfall erhalten wir als konvexe Hülle ein Rhombendodekaeder (Abb. 7).

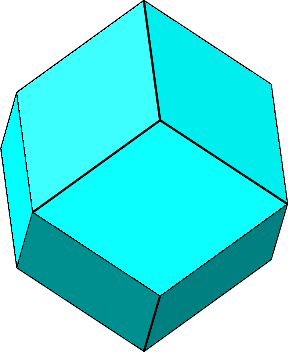
Abb. 7: Rhombendodekaeder

In der Endlage ist die konvexe Hülle das Oktaeder.

Weblinks

Hans Walser: Konvexe Hülle

https://walser-h-m.ch/hans/Miniaturen/K/Konvexe_Huelle2/Konvexe_Huelle2.html

Hans Walser: Konvexe Hülle

https://walser-h-m.ch/hans/Miniaturen/K/Konvexe_Huelle/Konvexe_Huelle.html