Hans Walser, [20231116]

Oktaeder-Knoten

Anregung: Gunter Weiß, Wien

1 Worum es geht

Flechtmodell mit nur einem Streifen für ein nicht ganz regelmäßiges Oktaeder

2 Das Oktaeder

Wir setzen acht rechtwinklig-gleichschenklige Dreiecke zu einem Oktaeder zusammen (Abb. 1 und 2).

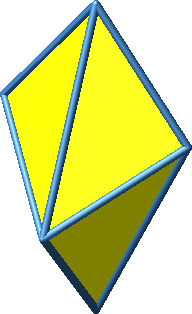
Abb. 1: Oktaeder

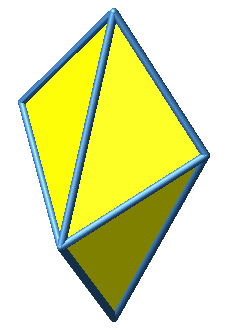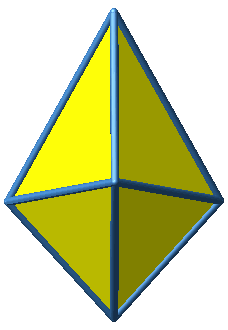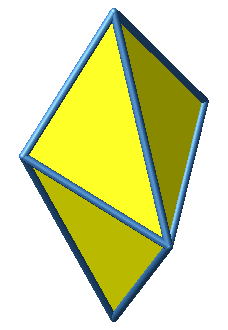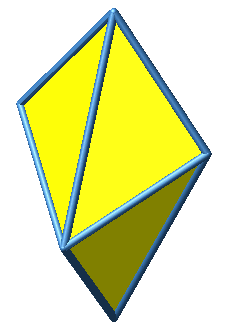
Abb. 2: Verschiedene Sichten

Dieses Oktaeder hat acht kurze und vier lange Kanten. Eine lange Kante ist √2-mal so lang wie eine kurze Kante. Die kurzen Kanten sind Katheten der rechtwinklig-gleichschenkligen Dreiecke, die langen Kanten Hypotenusen.

Wir bauen nun ein Flechtmodell für dieses Oktaeder.

3 Flechtmodell

Für das Flechtmodell genügt ein einziger Streifen (Abb. 3). Der Streifen besteht in der Theorie aus acht Quadraten, welche je eine diagonale Faltlinie haben.

In der Praxis geben wir zwei Quadrate dazu, die mit den ersten beiden zu „identifizieren“ sind. Ihre Überlagerung gibt dem Modell seine Stabilität. Weiter sind die Quadrate in der Praxis keine Quadrate, sondern etwa 3% weniger hoch als breit. Damit kann beim Flechten die Papierdicke berücksichtigt werden.

Abb. 3: Streifen für das Flechtmodell

Der Streifen wird ausgeschnitten und vorgefaltet. Der Autor hat mit festem Papier aus einem alten Querformat-Kalender gearbeitet.

Das Flechten geht wider Erwarten recht einfach. Es muss ein einziges Mal durchgeschlauft werden. Die Abbildung 4 zeigt drei Modelle.

Abb. 4: Flechtmodelle

4 Flechtstruktur

In der Abbildung 5 ist der Streifen in der Breite auf das mittlere Fünftel reduziert dargestellt. Damit wird die Flechtstruktur sichtbar. Der Streifen kreuzt sich auf den vier langen Kanten des Oktaeders.

Abb. 5: Flechtstruktur

Die Abbildung 6 zeigt die topologische Flechtstruktur als Knoten dargestellt.

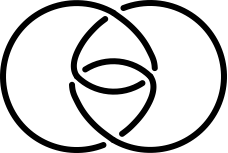
Abb. 6: Oktaeder-Knoten

5 Abwicklungen

Die Abbildungen 7 und 8 zeigen links je eine Abwicklung unseres Oktaeders und rechts die topologisch äquivalente Abwicklung des regelmäßigen Oktaeders. Die Abwicklung der Abbildung 7 entspricht dem halben theoretischen Flechtstreifen.

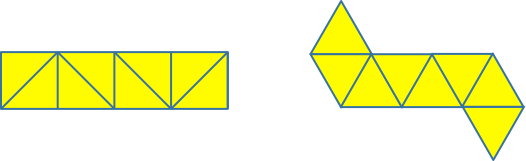
Abb. 7: Abwicklung

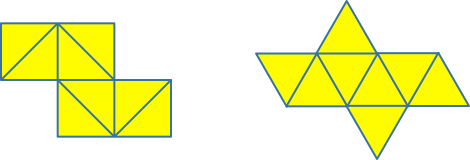
Abb. 8: Eine andere Abwicklung

Weblink

Hans Walser: Goldener Schnitt

https://walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_13/Goldener_Schnitt_13.html