Hans Walser, [20240712]
Oktaedertransformation
1 Worum es geht
Abschleifen eines regelmäßigen Oktaeders
Regelmäßiges Ikosaeder und gekerbtes Ikosaeder
Kuboktaeder
Goldene Axt und Großes Ikosaeder
Räumliches Gelenkmodell mit gleichseitigen Dreiecken
2 Die Transformation

Abb. 1: Transformation

Abb. 2: Im Oktaeder
Die Figur ist parametrisiert wie folgt. Die Kantenlänge des Oktaeders wird auf 1 normiert. Der Parameter t legt die Eckpunkte der kleinen roten Dreiecke fest. Für t = 0 haben wir das Start-Oktaeder, für t = 1 das End-Oktaeder.
Im Folgenden einige Sonderfälle. In den Abbildungen 1 und 2 sind sie als Boxenstopps hervorgehoben.
2.1 Oktaeder
Für t = 0 und t = 1 ergibt sich je ein regelmäßiges Oktaeder.
2.2 Ikosaeder
Für t = 1 – 1/ Φ ≈ 0.382 ergibt sich erhalten wir das regelmäßige Ikosaeder (Abb. 3). Dabei ist Φ = (1 + √(5))/2 ≈ 1.618 der Goldene Schnitt.

Abb. 3: Regelmäßiges Ikosaeder
2.3 Kuboktaeder
Für t = ½ erhalten wir das Kuboktaeder (Abb. 4). Dabei muss man ein Auge zudrücken und übersehen, dass die gelben Seitenquadrate aus je zwei rechtwinklig gleichschenkligen Dreiecken zusammengesetzt sind. Wir haben „blinde Kanten“.

Abb. 4: Kuboktaeder
2.4 Gekerbtes Ikosaeder
Für t = 1/Φ ≈ 0.618 ergibt sich das gekerbte Ikosaeder (Abb. 5).

Abb. 5: Gekerbtes Ikosaeder
Die Ecken des gekerbten Ikosaeders sind dieselben wie jene des regulären Ikosaeders. Von den Kanten entsprechen 24 denen des Ikosaeders. Sechs Kanten sind länger. Ihre Kantenlänge ist das Φ-fache der Kantenlänge des Ikosaeders. Insgesamt haben wir 30 Kanten, wie beim Ikosaeder. Acht Seitenflächen sind regelmäßige Dreiecke wie beim Ikosaeder. Die restlichen zwölf Seitenflächen sind gleichschenklige Dreiecke. Deren Basislänge ist das Φ-fache der Schenkellänge. Es handelt sich um sogenannte Stumpfe Goldene Dreiecke. Insgesamt haben wir 20 Seitenflächen, wie beim Ikosaeder.
3 Abschleifen
Der Transformationsprozess vom Oktaeder zu einer partikulären aber nicht speziellen Figur geschieht durch Abschleifen (Abb. 6 für t = 0.2). Die gelben Dreiecke entstehen durch dieses Abschleifen.

Abb. 6: Abschleifen
3.1 Ikosaeder

Abb. 7: Abschleifen zum Ikosaeder
3.2 Kuboktaeder
Beim Kuboktaeder entspricht der Abschleifprozess dem Abstumpfen der Ecken (Abb. 8).

Abb. 8: Abschleifen zum Kuboktaeder. Abstumpfen der Ecken
Der Abschleifprozess muss für jede partikuläre aber nicht spezielle Figur extra gemacht werden. So kann zum Beispiel nicht das Ikosaeder durch Weiterschleifen zum Kuboktaeder gemacht werden. Das Ikosaeder kann lediglich zum gekerbten Ikosaeder zugeschliffen werden.
4 Überziehen
Unser Parameter t variiert im Intervall 0 ≤ t ≤ 1. Natürlich ist man versucht, das Intervall zu überziehen. Beim Intervall –Φ ≤ t ≤ Φ2 (Abb. 9) ergeben sich interessante Endfiguren.

Abb. 9: Überziehen
4.1 Goldene Axt
Für t = –Φ erhalten wir die Goldene Axt (Abb. 10 und Abb. 11). Die gelben Dreiecke sind gleichschenklige, ihre Schenkellänge ist das Φ-fache der Basislänge. Es handelt sich um sogenannte Spitze Goldene Dreiecke.

Abb. 10: Goldene Axt

Abb. 11: Goldene Axt
4.2 Großes Ikosaeder
Für t = Φ2 ≈ 2.618 ergibt sich das Große Ikosaeder (Abb. 12 und Abb. 13). Die gelben Dreiecke sind gleichseitig und kongruent zu den roten. Insgesamt haben wir 20 gleichseitige Dreiecke.
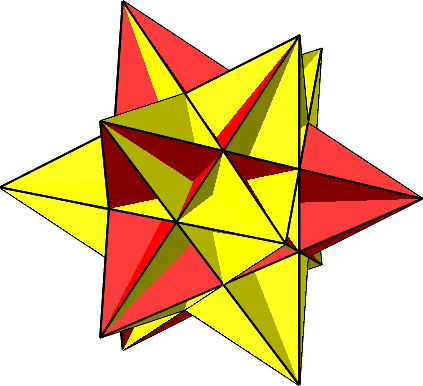
Abb. 12: Großes Ikosaeder

Abb. 13: Großes Ikosaeder
Weblinks
Hans Walser: Goldener Schnitt
https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html
Hans Walser: Ikosaeder
https://walser-h-m.ch/hans/Miniaturen/I/Ikosaeder3/Ikosaeder3.html
Literatur
Walser, Hans (2024): Der Goldene Schnitt.
Geometrische und zahlentheoretische Betrachtungen. 7. Auflage. Springer
Spektrum.
Print-ISBN 978-3-662-68556-3. E-Book_ISBN
978-3-662-68557-0.
https://doi.org/10.1007/978-3-662-68557-0