Hans Walser, [20231130]

Origami-Tetraeder

1 Worum es geht

Regelmäßiges Tetraeder mit zwei Bauteilen durch Falten und Schneiden.

2 Zuschnitt eines Bauteils

Wir beginnen mit einem rechteckigen Papier im Querformat (Abb. 1a). Ich habe mit DIN A4 gearbeitet, es geht aber auch mit zum Beispiel US Letter.

Aus didaktischen Gründen wird in den folgenden Figuren angenommen, das Papier sei auf der Vorderseite gelb und auf der Rückseite hellblau.

Wir falten die Mittellinie und auf der linken Seite nochmals die Mittellinie (Abb. 1b).

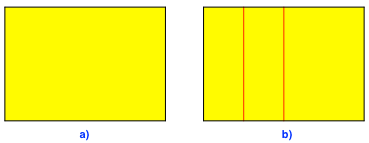
Abb. 1: Start

Nun falten wir die rechte obere Ecke auf die Mittellinie in der linken Hälfte. Dabei soll die Faltlinie in der Mitte der Oberkante des Papiers beginnen, also am oberen Ende der Mittellinie des Gesamtpapiers (Abb. 2a). Nach dem Zurückfalten haben wir eine schräge Faltlinie mit dem Steigungswinkel 60° (Abb. 2b).

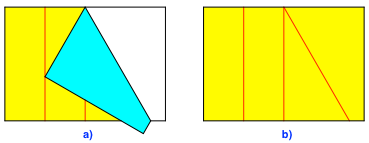
Abb. 2: Ecke herunterfalten und wieder zurück

Auf der anderen Seite machen wir dasselbe (Abb. 3). Wir erhalten ein gleichseitiges Dreieck.

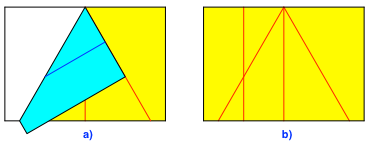
Abb. 3: Dasselbe auf der anderen Seite

Nun wird das Prozedere von unten wiederholt (Abb. 4 und 5).

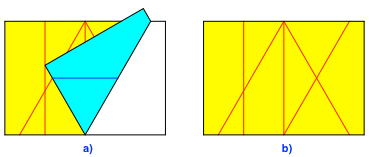
Abb. 4: Dasselbe von unten rechts

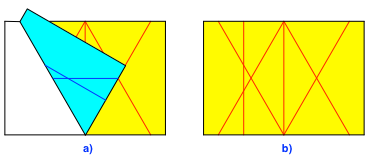
Abb. 5: Dasselbe von unten links

Wir erhalten ein zweites gleichseitiges Dreieck, es hat die Spitze nach unten.

Wir schneiden die Restteile links und rechts weg (Abb. 6a). Dies kann so geschehen, dass man nochmals einfaltet und mit einem Taschenmesser bis zur Mitte einschneidet.

Schließlich falten wir die horizontale Mittellinie (Abb. 6b).

Abb. 6: Ausschneiden und falten

Es bleibt eine technisch bedingte Faltkante sichtbar, welche später nicht mehr benötigt wird. Allerdings verschwindet diese Faltkante im fertigen Modell im Innern und ist dann nicht mehr sichtbar.

3 Falten der Laschen und Taschen

Aus den vier kleinen gleichseitigen Dreiecken in den Ecken falten wir die Laschen (Abb. 7) und Taschen (Abb. 8 und 9). Die Taschen dienen zur Aufnahme der Laschen.

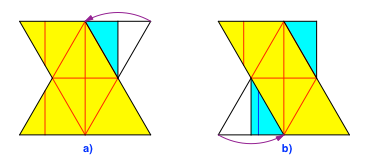
Abb. 7: Laschen

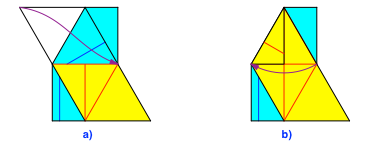
Abb. 8: Tasche links oben

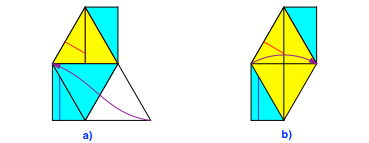
Abb. 9: Tasche rechts unten

4 Zwei Bauteile

Wir benötigen zwei spiegelbildliche Bauteile. Das eine Bauteil (rosa in Abb. 10) gemäß der Abbildung 9b, das andere (hellblau in Abb. 10) spiegelbildlich dazu.

Abb. 10: Zwei spiegelbildliche Bauteile

5 Montage

Die beiden Bauteile sind (bis auf die Laschen) Rhomben, welche aus zwei gleichseitigen Dreiecken zusammengesetzt sind. An den Ecken haben wir daher Winkel von 60° und von 120°. Bei der Montage muss jede Ecke von 60° auf eine Ecke von 120° treffen. Die Abbildung 11 zeigt die Ausgangslage der Montage.

Abb. 11: Spitze Ecke auf stumpfe Ecke

Die Lasche rechts oben des rosa Bauteils passt nun die die Tasche links oben des hellblauen Bauteils. Umgekehrt passt die Lasche links unten des hellblauen Bauteils in die Tasche rechts unten des rosa Bauteils.

6 Origami-Tetraeder

Mit etwas Fingerspitzengefühl bringen wir auch die restlichen Laschen in die richtigen Taschen und erhalten das Tetraeder-Modell (Abb. 12).

Abb. 12: Tetraeder-Modell

7 Symmetrie

Das Origami-Tetraeder-Modell hat viel weniger Symmetrien als das (abstrakte) regelmäßige Tetraeder. Die Abbildung 13 zeigt die einzige noch verbliebene Symmetrieachse (zweizählige Drehsymmetrie).

Abb. 13: Zweizählige Drehsymmetrie-Achse

Weblinks

Hans Walser: Origami-Oktaeder

https://walser-h-m.ch/hans/Miniaturen/O/Origami-Oktaeder/Origami-Oktaeder.html

Hans Walser: Origami-Tetraeder

https://walser-h-m.ch/hans/Miniaturen/O/Origami-Tetraeder/Origami-Tetraeder.htm