*Hans Walser, [20250316]

Parameterbereiche

1 Worum es geht

Verschiedene Kugeldarstellungen

2 Abbildungsgleichungen

Wir arbeiten durchgehend mit den Abbildungsgleichungen:

x₁ = cos(ϕ) cos(λ)

x₂ = cos(ϕ) sin(λ)

x₃ = sin(ϕ)

3 Klassische Parametrisierung

In der klassischen Parametrisierung der Einheitskugel bedeuten ϕ ∈ [–π/2, π/2] und λ ∈ [–π, π] die geografische Breite beziehungsweise die geografische Länge (Abb. 1).

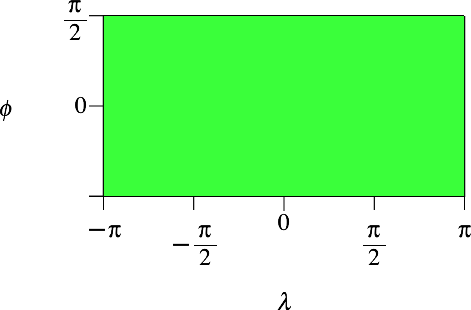
Abb. 1: Geografische Breite ϕ und geografische Länge λ

4 Zonen

Die Darstellung mit verschieden gefärbten Zonen erleichtert die Einsicht in den Zusammenhang zwischen dem Parameterbereich und der Kugel.

4.1 Meridianzonen

Wir arbeiten mit acht Meridianzonen (Abb. 2 und Abb. 3). Im Parameterbereich sind dies acht nebeneinanderstehende Rechtecke, auf der Kugel acht „Schnitze“.

Abb. 2: Meridianzonen

Abb. 3: Meridianzonen

Die 24 Zeitzonen auf der Erdkugel sind ebenfalls Meridianzonen.

4.2 Breitenkreiszonen

Wir arbeiten mit acht Breitenkreiszonen (Abb. 4 und Abb. 5). Im Parameterbereich sind dies acht aufeinanderliegende kongruente Rechtecke, auf der Kugel acht Zonen ungleicher Größe.

Abb. 4: Breitenkreiszonen

Abb. 5: Die Kugel dreht sich, aber man merkt es kaum

Die Klimazonen auf der Erdkugel sind Breitenkreiszonen.

5 Hochformat

Wir arbeiten nach wie vor mit den Abbildungsgleichungen:

x₁ = cos(ϕ) cos(λ)

x₂ = cos(ϕ) sin(λ)

x₃ = sin(ϕ)

aber mit dem Parameterbereich im Hochformat, also ϕ ∈ [–π, π] und λ ∈ [–π/2, π/2]. Dies irritiert, funktioniert aber auch (Abb. 6).

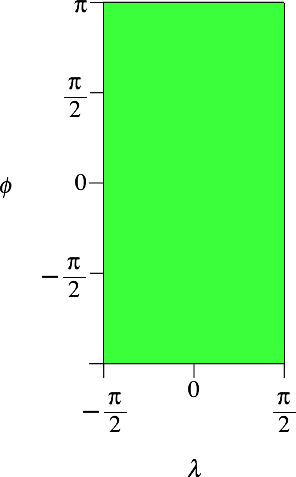
Abb. 6: Parameterbereich im Hochformat

6 Zonen

Der Unterschied zur Querformat-Parametrisierung zeigt sich, wenn wir mit Zonen arbeiten.

6.1 Meridianzonen

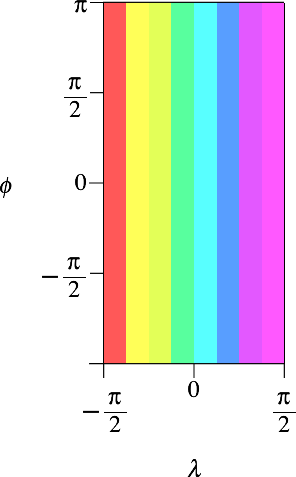
Abb. 7: Meridianzonen

Jede Farbe erscheint zweimal (Abb. 8). Gleichfarbige „Schnitze“ liegen symmetrisch zur Erdachse.

Abb. 8: Jede Farbe kommt zweimal vor

Wir können, wenn man so will, zwischen AM und PM unterscheiden.

6.2 Breitenkreiszonen

Die Breitenkreiszonen sind auf der Kugel nicht durchgehend (Abb. 9 und Abb. 10). Wir sehen einen harten Schnitt zwischen der Vorderseite und der Rückseite. Die mittleren vier Zonen sind nur auf der Vorderseite lokalisiert, die anderen vier Zonen nur auf der Rückseite.

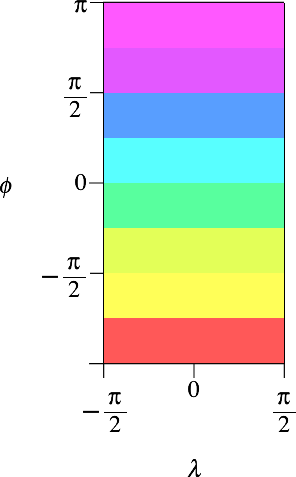
Abb. 9: Breitenkreiszonen

Abb. 10: Harter Schnitt zwischen Vorderseite und Rückseite

7 Transformation

7.1 Vom Querformat zum Hochformat

Wir transformieren den Parameterbereich vom Querformat zum Hochformat (Abb. 11). Für jede Zwischensituation des Parameterbereiches zeichnen wir durch die Abbildungsgleichungen definierte Figur. In der Start- und in der Endsituation haben wir die volle Kugeloberfläche. Für die Zwischensituationen ergeben sich Löcher auf der Rückseite der Kugeloberfläche.

Abb. 11: Vom Querformat zum Hochformat

Auf der Vorderseite der Kugel passiert nichts, auf der Rückseite einiges (Abb. 12).

Abb. 12: Vorderseite und Rückseite

7.2 Meridianzonen

Abb. 13: Meridianzonen im Parameterbereich

Abb. 14: Meridianzonen

Zwei benachbarte Farben überkreuzen sich an den Polen.

7.3 Breitenkreiszonen

Abb. 15: Breitenkreiszonen im Parameterbereich

Abb. 16: Breitenkreiszonen

Weblinks

Hans Walser, Parameterbereiche

https://walser-h-m.ch/hans/Miniaturen/P/Parameterbereiche/Parameterbereiche.html