Hans Walser, [20240612]
Poncelet
Anregung: Wilfried Dutkowski, Bonn
1 Worum es geht
Sonderfälle des Satzes von Poncelet. Symmetrie
2 Der Satz von Poncelet
Die Abbildung 1 zeigt zwei Ellipsen und ein Viereck, welches der äußeren Ellipse einbeschrieben und der inneren Ellipse umbeschrieben ist.
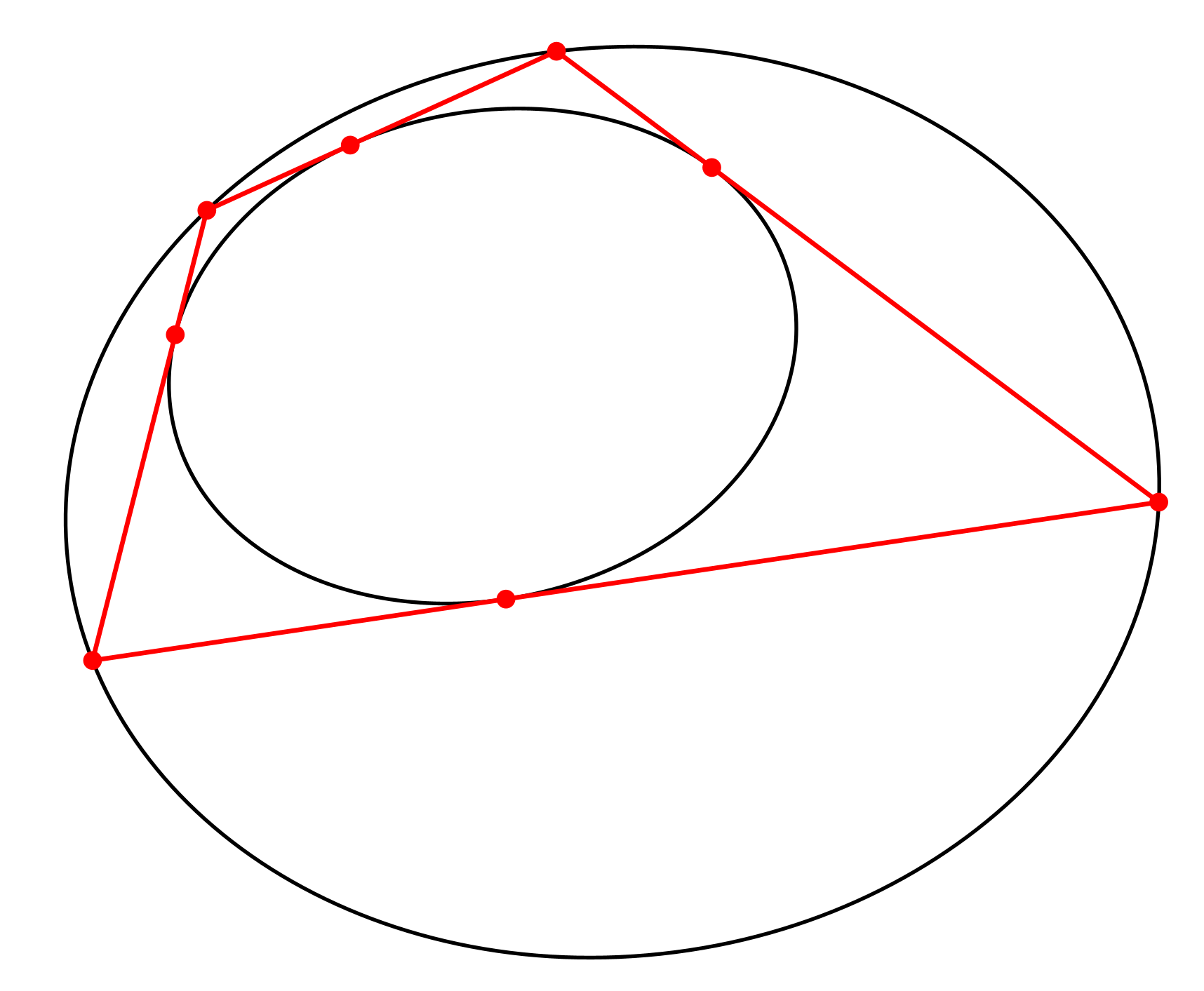
Abb. 1: Viereck mit Umellipse und Inellipse
Nach dem Satz von Poncelet gibt es in dieser Situation unendlich viele Vierecke, welche der äußeren Ellipse einbeschrieben und der inneren Ellipse umbeschrieben sind (Abb. 2).
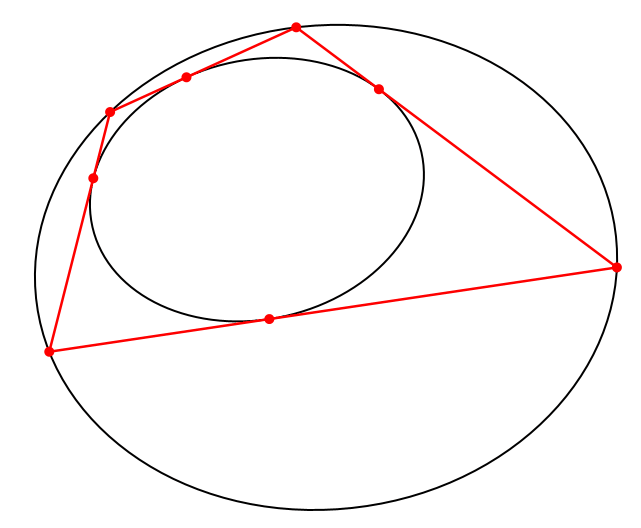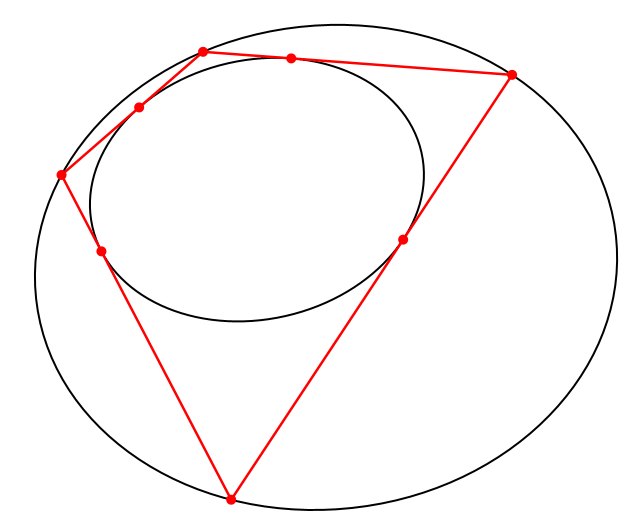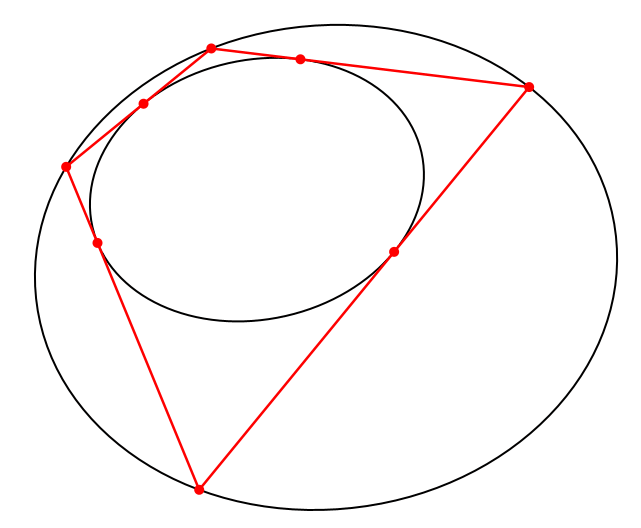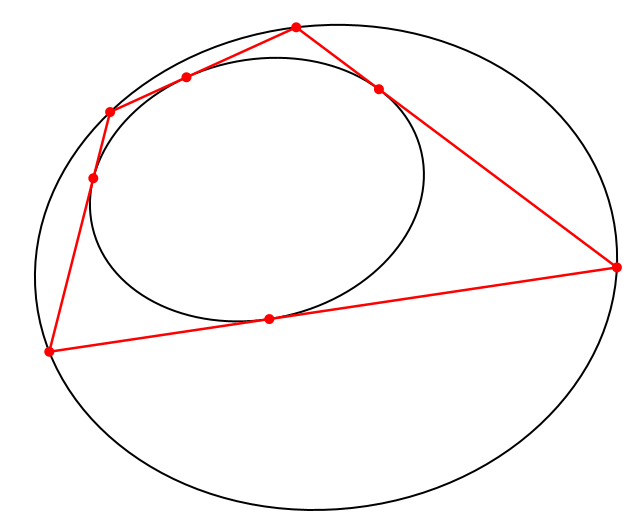
Abb. 2: Weitere passende Vierecke
Der Satz von Poncelet gilt nicht nur für Vierecke, sondern allgemein für n-Ecke mit n ≥ 3.
3 Spezielle Ellipsenlage
Die Abbildung 3 zeigt nun eine spezielle relative Lage der beiden Ellipsen. Sie haben dieselben Symmetrieachsen. Die aus den beiden Ellipsen bestehende Figur ist punktsymmetrisch.
Der eingezeichnete Rhombus ist der äußeren Ellipse einbeschrieben und der inneren Ellipse umbeschrieben.
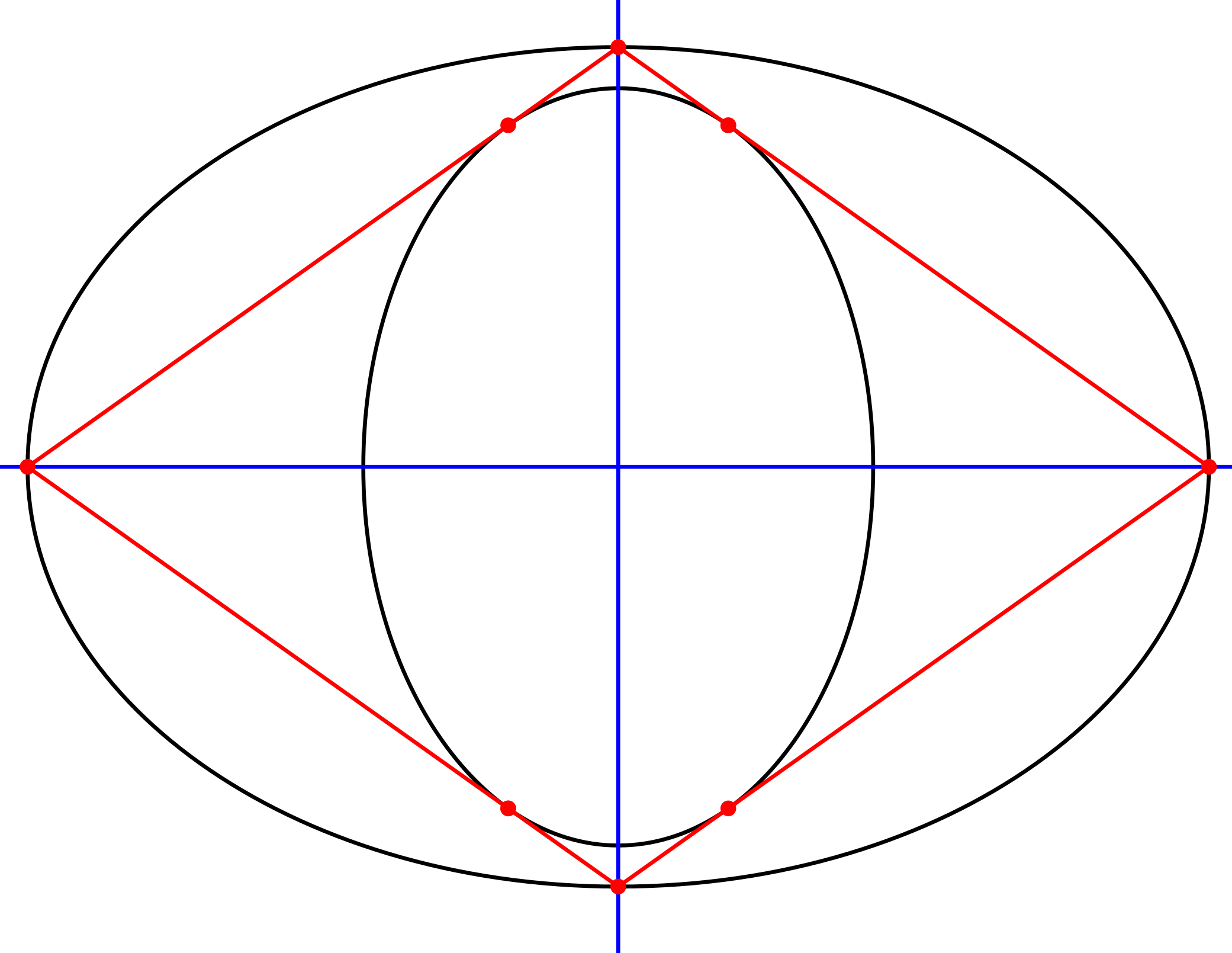
Abb. 3: Spezielle Lage der Ellipsen
Nach dem Satz von Poncelet gibt es unendlich viele Vierecke, welche der äußeren Ellipse einbeschrieben und der inneren Ellipse umbeschrieben sind (Abb. 4).
Wegen der Punktsymmetrie der Ellipsenkonfiguration sind die Vierecke ebenfalls punktsymmetrisch. Sie sind also Parallelogramme.
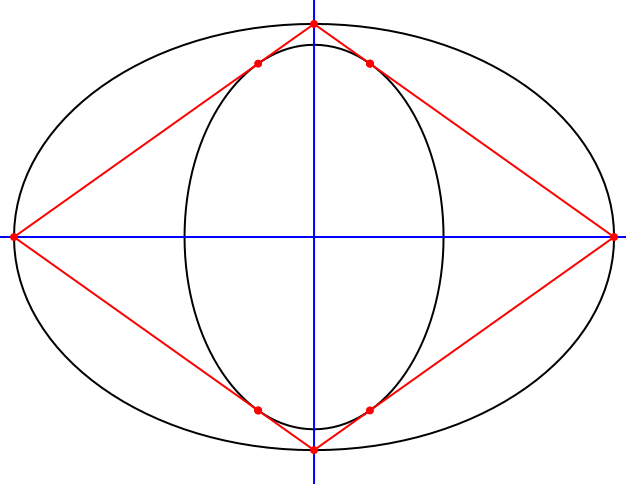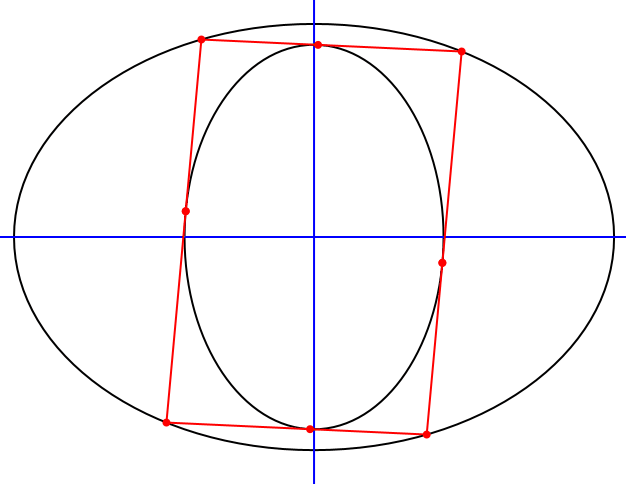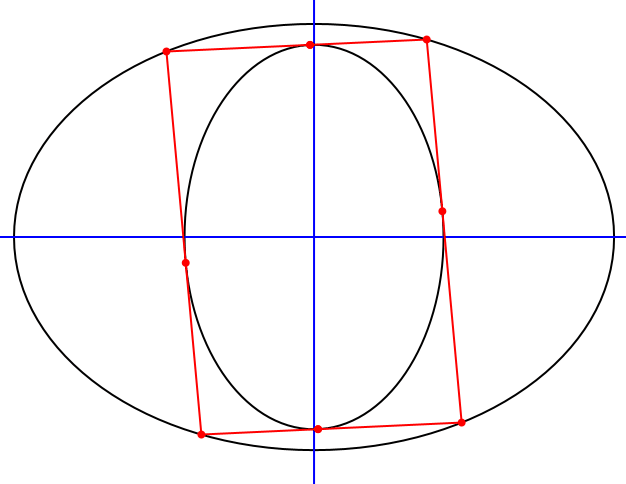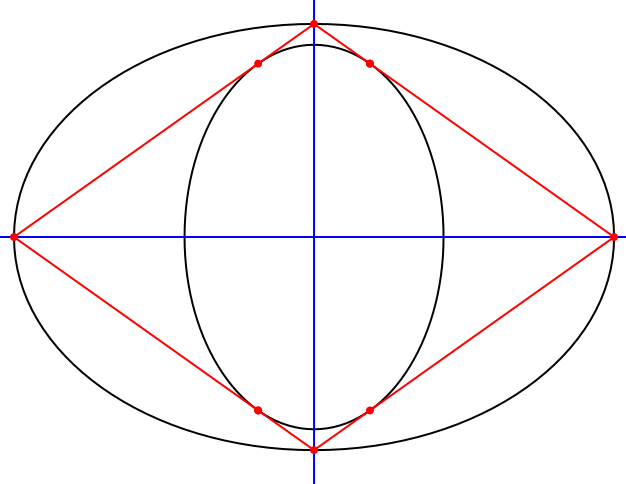
Abb. 4: Parallelogramme
4 Umkreis
In der Abbildung 5 ist die äußere Ellipse ein Kreis.
Zwischen den Halbachsen a und b der inneren Ellipse und dem Radius r des Kreises besteht die Beziehung:
r2 = a2 + b2
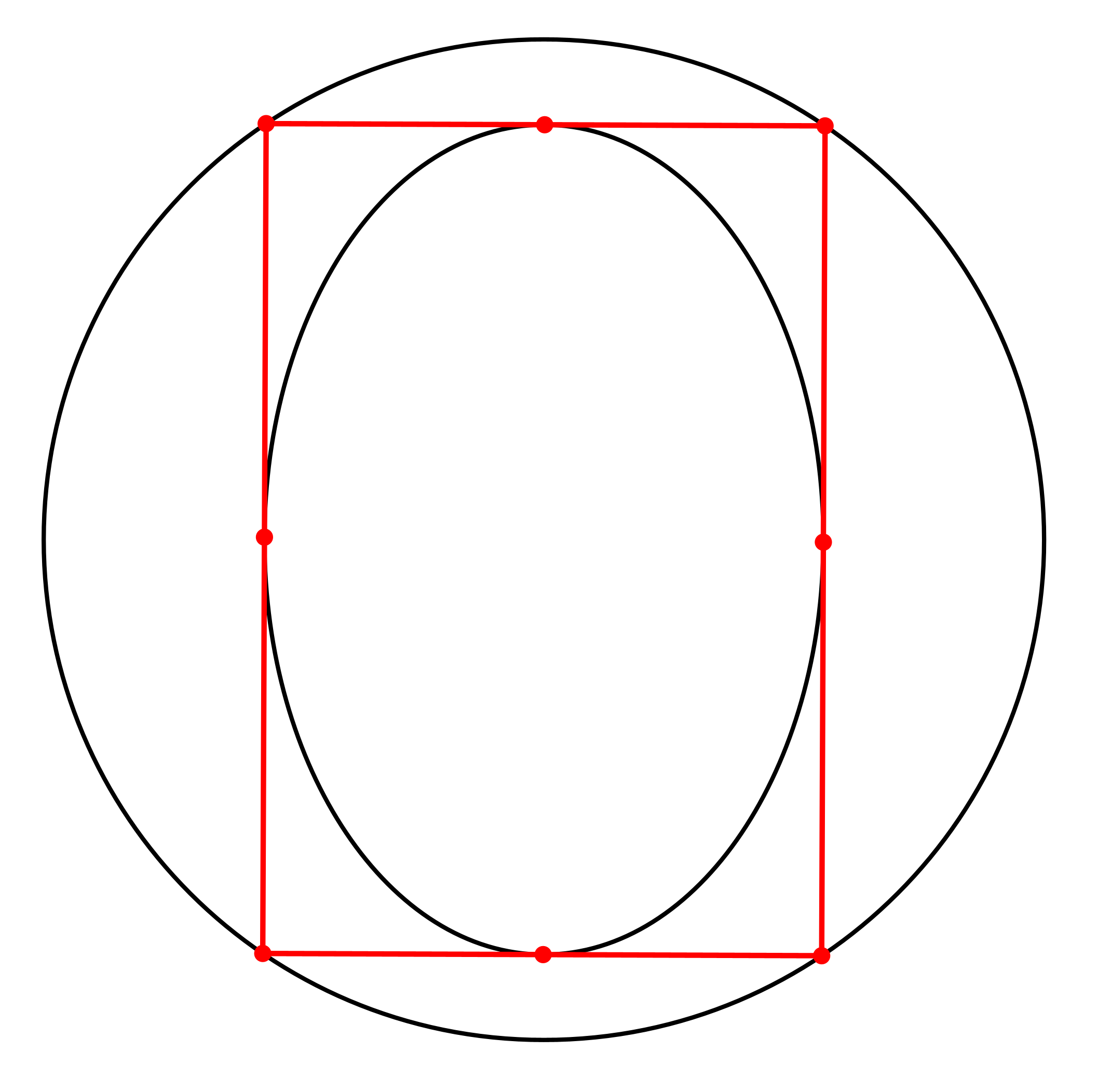
Abb. 5: Umkreis
Die weiteren Lösungen sind Parallelogramme mit einem Umkreis, also Rechtecke (Abb. 6).
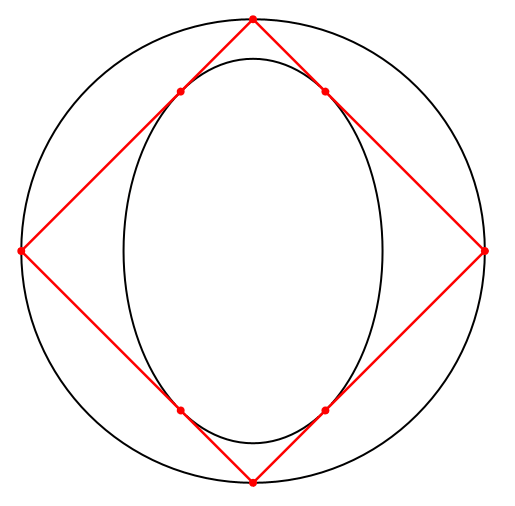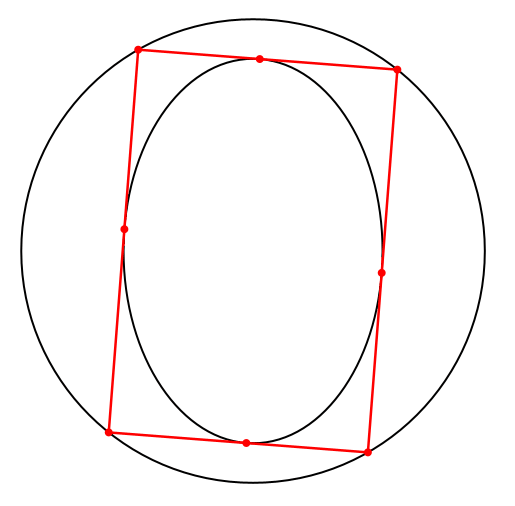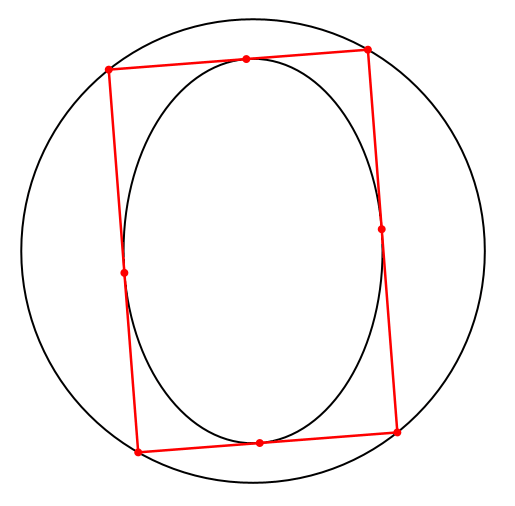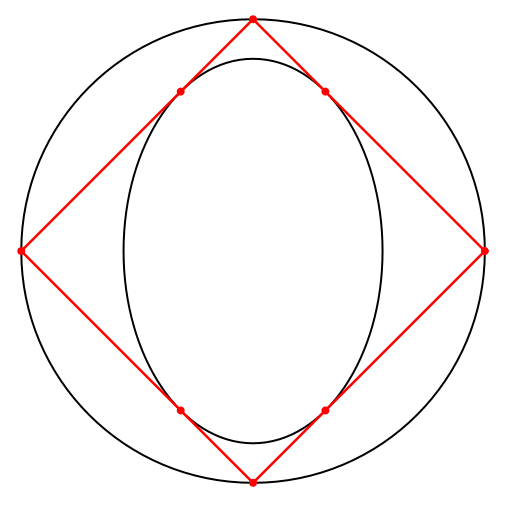
Abb. 6: Rechtecke
Wir können die innere Ellipse speziell als Strecke zeichnen. Dann ergibt sich der Thaleskreis (Abb. 7).
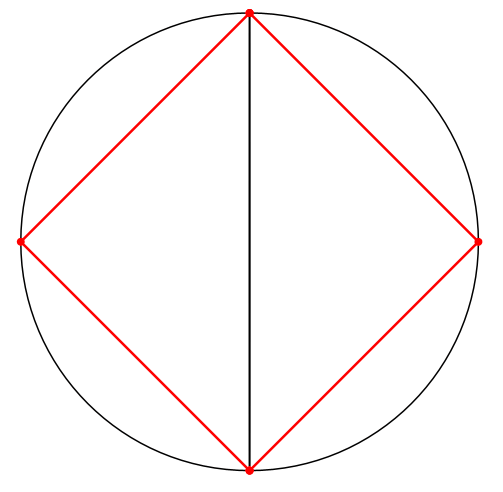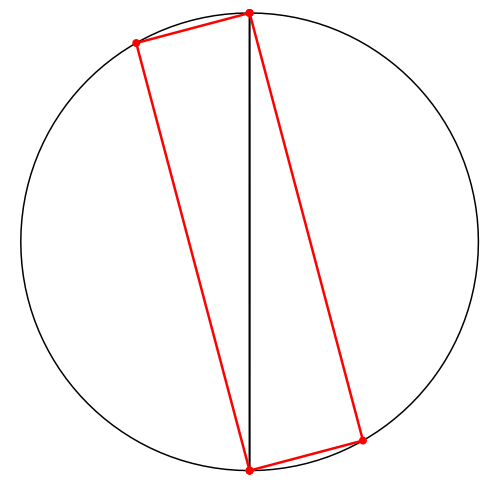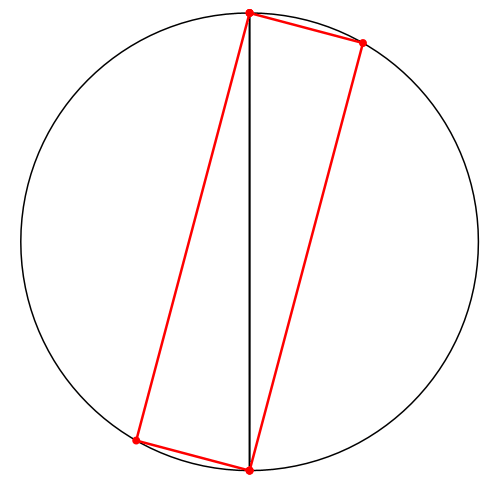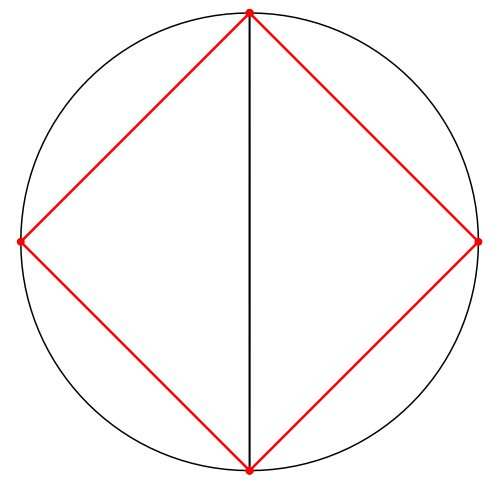
Abb. 7: Thaleskreis
5 Inkreis
In der Abbildung 8 ist die innere Ellipse ein Kreis.
Zwischen den Halbachsen a und b der äußeren Ellipse und dem Radius r des Kreises besteht die Beziehung:
1/r2 = 1/a2 + 1/b2
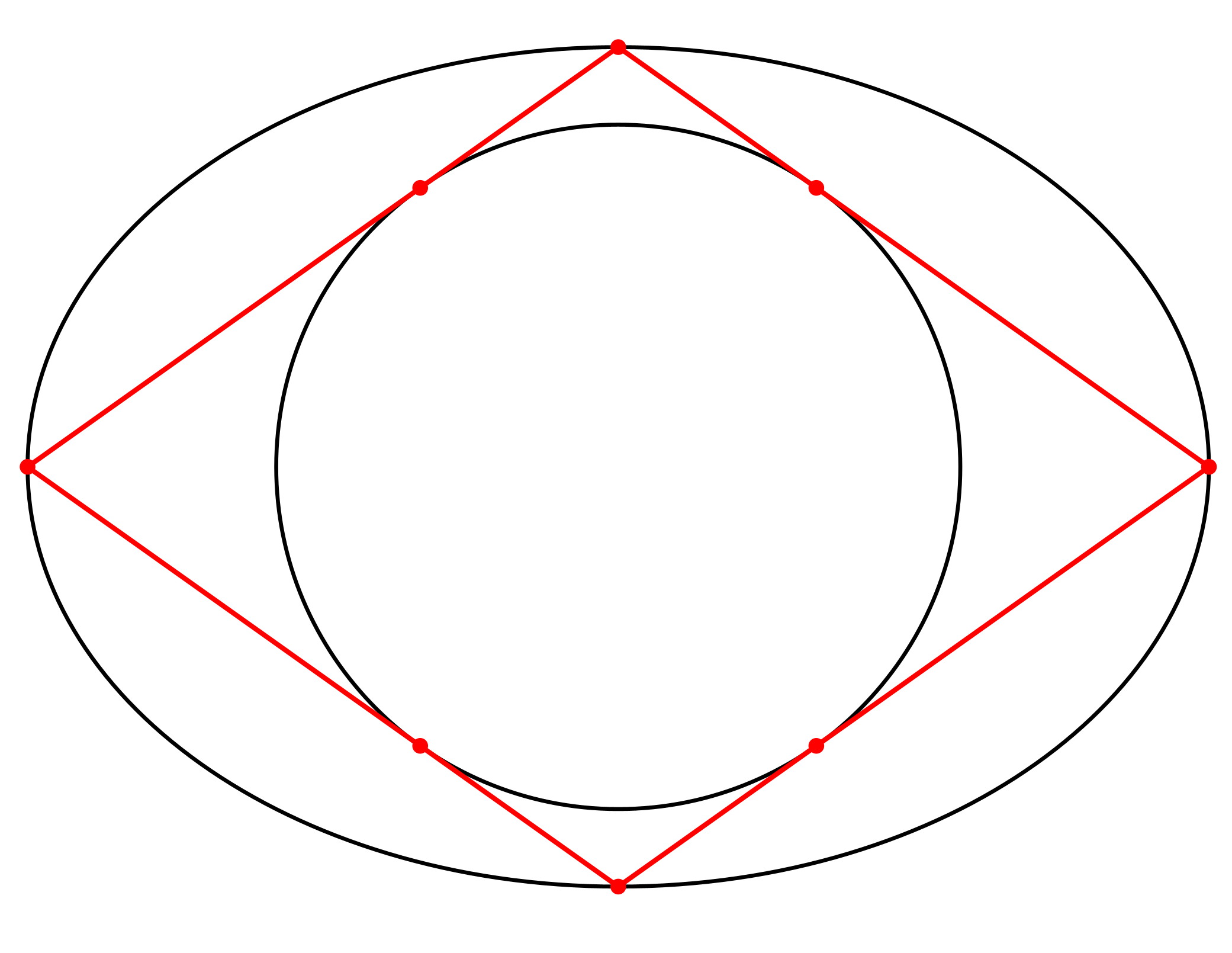
Abb. 8: Inkreis
Die weiteren Lösungen sind Parallelogramme mit einem Inkreis, also Rhomben (Abb. 9).
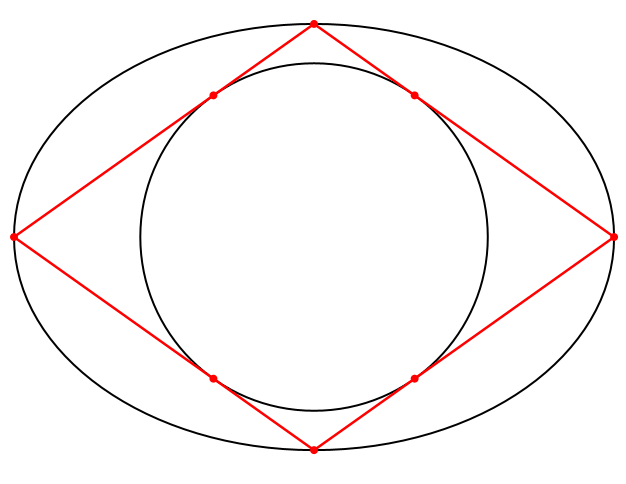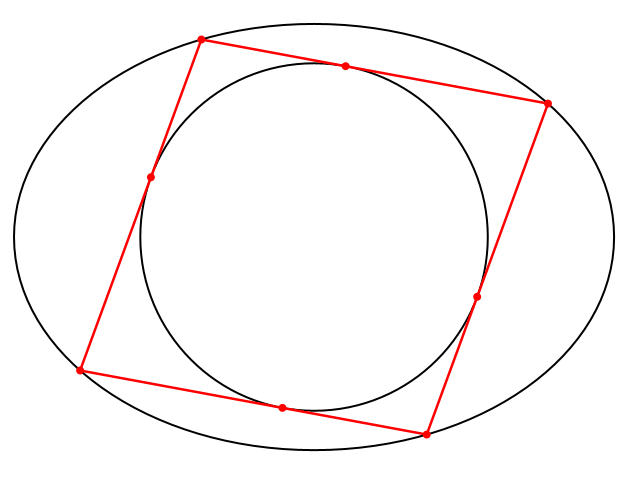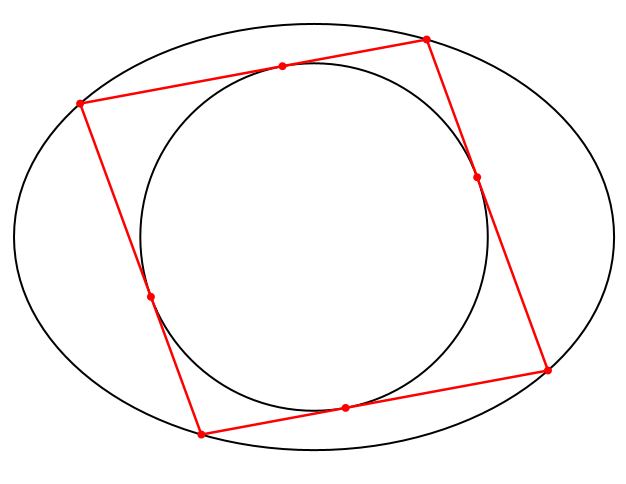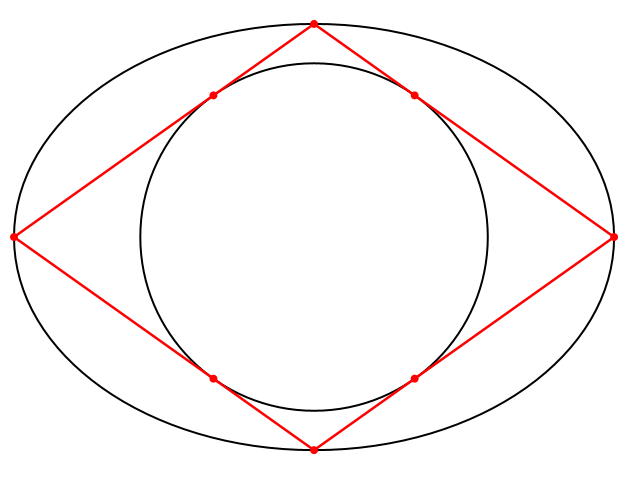
Abb. 9: Rhomben
6 Um- und Inkreis
Der Pedanterie halber innen und außen ein Kreis (Abb. 10). Die beiden Kreisradien stehen im Verhältnis √2 : 1.
Die Lösungen sind Parallelogramme mit einem Umkreis und einem Inkreis, also Quadrate.
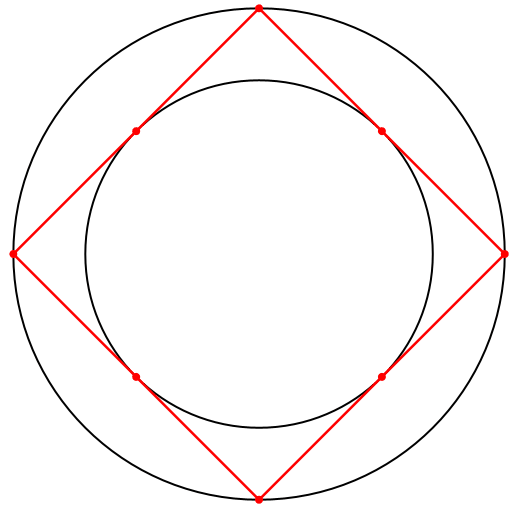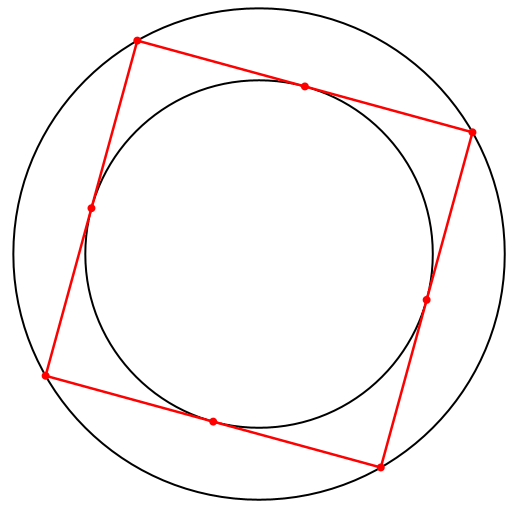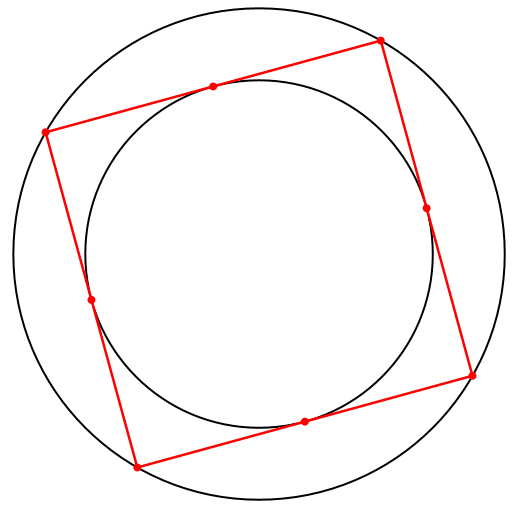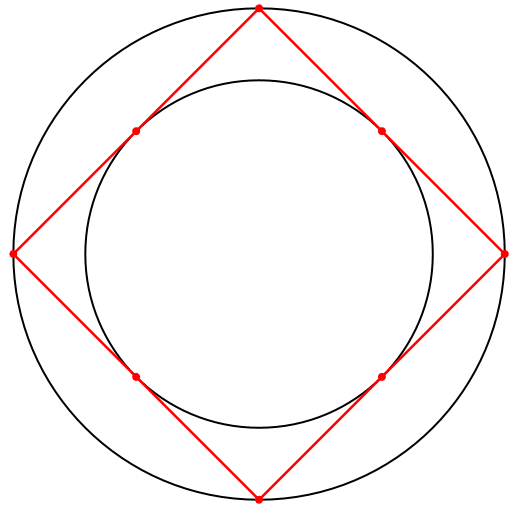
Abb. 10: Zwei Kreise
7 Person
Jean-Victor Poncelet, 1788-1867, französischer Mathematiker.
Weblinks
Hans Walser: Thaleskreis an Ellipse und Hyperbel
https://walser-h-m.ch/hans/Miniaturen/T/Thaleskreis_E_H/Thaleskreis_E_H.htm