Hans Walser, [20240922]

Quadrate im Kreis

1 Worum es geht

Dem Einheitskreis werden aus Quadraten zusammengesetzte Figuren einbeschrieben.

Flächeninhalt. Kombinatorik. Invariante.

2 Problemstellung

Die Abbildung 1 zeigt eine Figurenserie mit erkennbarer Systematik.

Abb. 1: Figurenserie

Die Abbildung 2 zeigt dasselbe als Animation.

Abb. 2: Animation

Der Kreis ist der Einheitskreis, hat also den Radius 1.

Wir groß ist die Gesamtfläche der durch die Quadrate gebildeten Figur?

3 Beispiele

3.1 Ein Quadrat

Ein einziges Quadrat (Abb. 3.1) hat die Seitenlänge √2 und damit den Flächeninhalt A = 2.

Abb. 3.1: Ein Quadrat

3.2 Fünf Quadrate

Bei fünf Quadraten in der Anordnung der Abbildung 3.2 hat jedes Einzelquadrat die Seitenlänge 2/√10 und damit den Flächeninhalt 2/5. Der gesamte Flächeninhalt A ist somit A = 2.

Abb. 3.2: Fünf Quadrate

3.3 Dreizehn Quadrate

Bei 13 Quadraten in der Anordnung der Abbildung 3.3 hat jedes Einzelquadrat die Seitenlänge 2/√26 und damit den Flächeninhalt 2/13. Der gesamte Flächeninhalt A ist somit A = 2.

Abb. 3.3: Dreizehn Quadrate

Wir vermuten, dass dieser gesamte Flächeninhalt A = 2 der Quadrate eine Invariante ist.

4 Beweis

Für den Beweis benötigen wir folgendes:

Eine geeignete Parametrisierung der Figuren

Anzahl der Quadrate in Abhängigkeit des Parameters

Flächeninhalt eines Einzelquadrates

4.1 Parametrisierung

Für die Parametrisierung verwenden wir die Anzahl n der Quadrate vom mittleren Quadrat bis zu einem Quadrat, welches den Kreis berührt. Das mittlere Quadrat wird mitgezählt.

Beispielsweise ist in der Abbildung 3.3 diese Anzahl n = 3.

Der „Durchmesser“ der Figur ist 2n – 1.

4.2 Anzahl der Quadrate

Zur Bestimmung der Anzahl der Quadrate drehen wir die Figur um 45° (Abb. 4 für n = 5).

Wir erkennen nun, dass die roten Quadrate in einem n×n-Quadratgitter angeordnet sind, die blauen Quadrate in einem (n – 1)×(n – 1)-Quadratgitter.

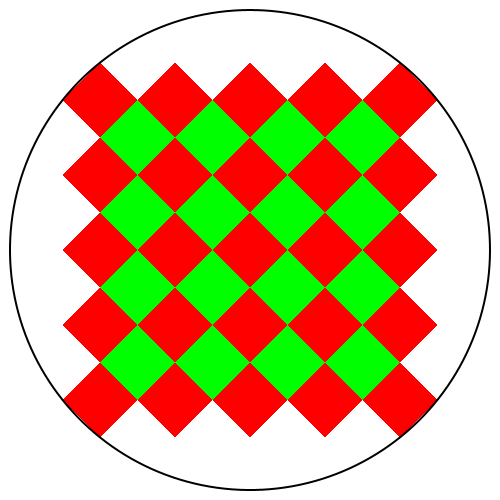
Abb. 4: Anordnung im Quadratgitter

Die gesamte Anzahl der Quadrate ist also n² + (n – 1)² = 2n² – 2n + 1.

4.3 Flächeninhalt eines Einzelquadrates

Wir suchen zunächst die Seitenlänge a eines Einzelquadrates. Dazu berechnen wir den eingezeichneten Durchmesser d des Kreises (Abb. 5).

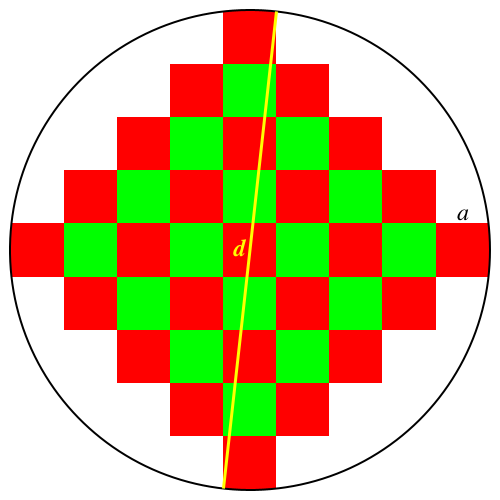
Abb. 5: Durchmesser

Nach dem Satz des Pythagoras ist:

d² = ((2n – 1) a)² + a² = a²(4n² – 4n + 2)

Wegen d² = 4 (Einheitskreis mit Durchmesser 2) folgt:

a² = 2 / (2n² – 2n + 1)

Nun ist aber a² der Flächeninhalt eines Einzelquadrates. Für die Gesamtfläche A der 2n² – 2n + 1 Einzelquadrate ergibt sich:

A = (2n² – 2n + 1) a² = 2 (2n² – 2n + 1) / (2n² – 2n + 1) = 2

Unsere Vermutung ist damit bewiesen.

Weblinks

Hans Walser: Goldener Schnitt im Kreuz

https://walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_im_Kreuz/Goldener_Schnitt_im_Kreuz.htm