1 Worum es geht

Im klassischen regelmäßigen Pentagramm schneiden sich die Seiten im Verhältnis des Goldenen Schnittes (Abb. 1). Rot zu blau verhält sich wie Φ : 1, mit Φ = (1 + √5)/2 ≈ 1.618 (Goldener Schnitt). Dieses Verhältnis ist irrational.

Abb. 1: Regelmäßiges Pentagramm

Die Frage ist, ob es ein (unregelmäßiges) Pentagramm mit rationalen Teilverhältnissen gibt.

2 Ganzzahlige Seitenverhältnisse

Wir zeichnen im Quadratraster das Pentagramm der Abbildung 2.

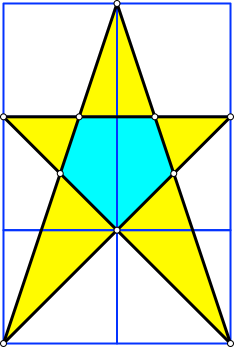
Abb. 2: Pentagramm im Quadratraster

Auf jeder Seite haben wir nun ganzzahlige Teilverhältnisse (Abb. 3). Dies kann mit Strahlensätzen eingesehen werden.

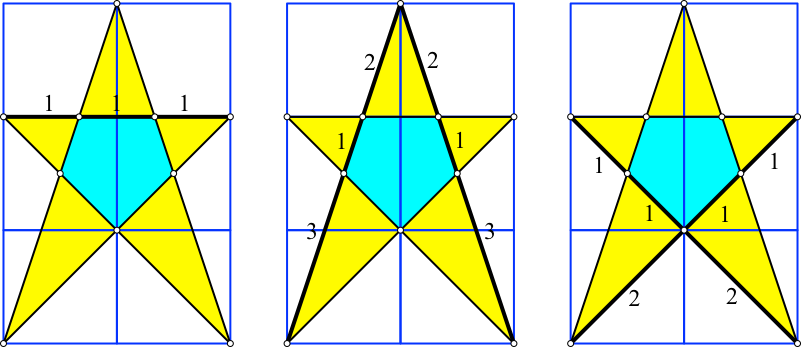
Abb. 3: Ganzzahlige Teilverhältnisse auf den Seiten

Die Teilverhältnisse sind aber nicht global rational. Die Abbildung 4 zeigt Strecken auf verschiedenen Seiten, welche im irrationalen Verhältnis √10 : 2 stehen.

Abb. 4: Irrationales Teilverhältnis

3 Global ganzzahlige Teilverhältnisse

Die Abbildung 5 zeigt eine Lösung mit global ganzzahligen Teilverhältnissen. Die Lösung basiert auf dem pythagoreischen Dreieck mit dem Seitenverhältnis 3 : 4 : 5.

Wir können die Figur aus Lochstreifen mit standardisiertem Lochabstand zusammenschrauben. Allerdings braucht es ziemlich lange Lochstreifen.

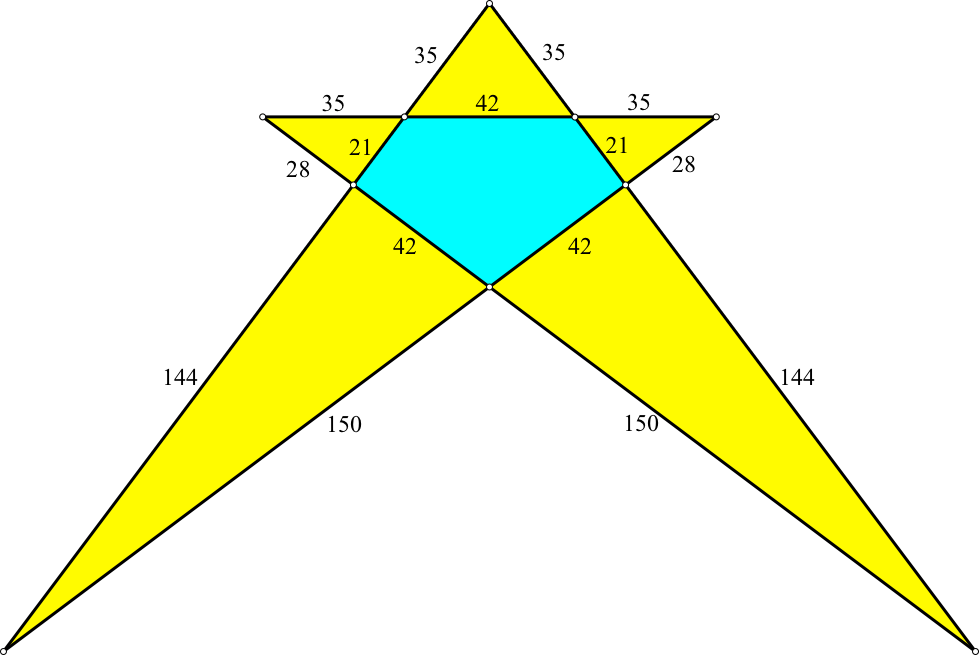
Abb. 5: Global ganzzahlige Teilverhältnisse

Die Abbildung 6 zeigt eine verwandte Konfiguration. Sie basiert ebenfalls auf dem pythagoreischen Dreieck mit dem Seitenverhältnis 3 : 4 : 5.

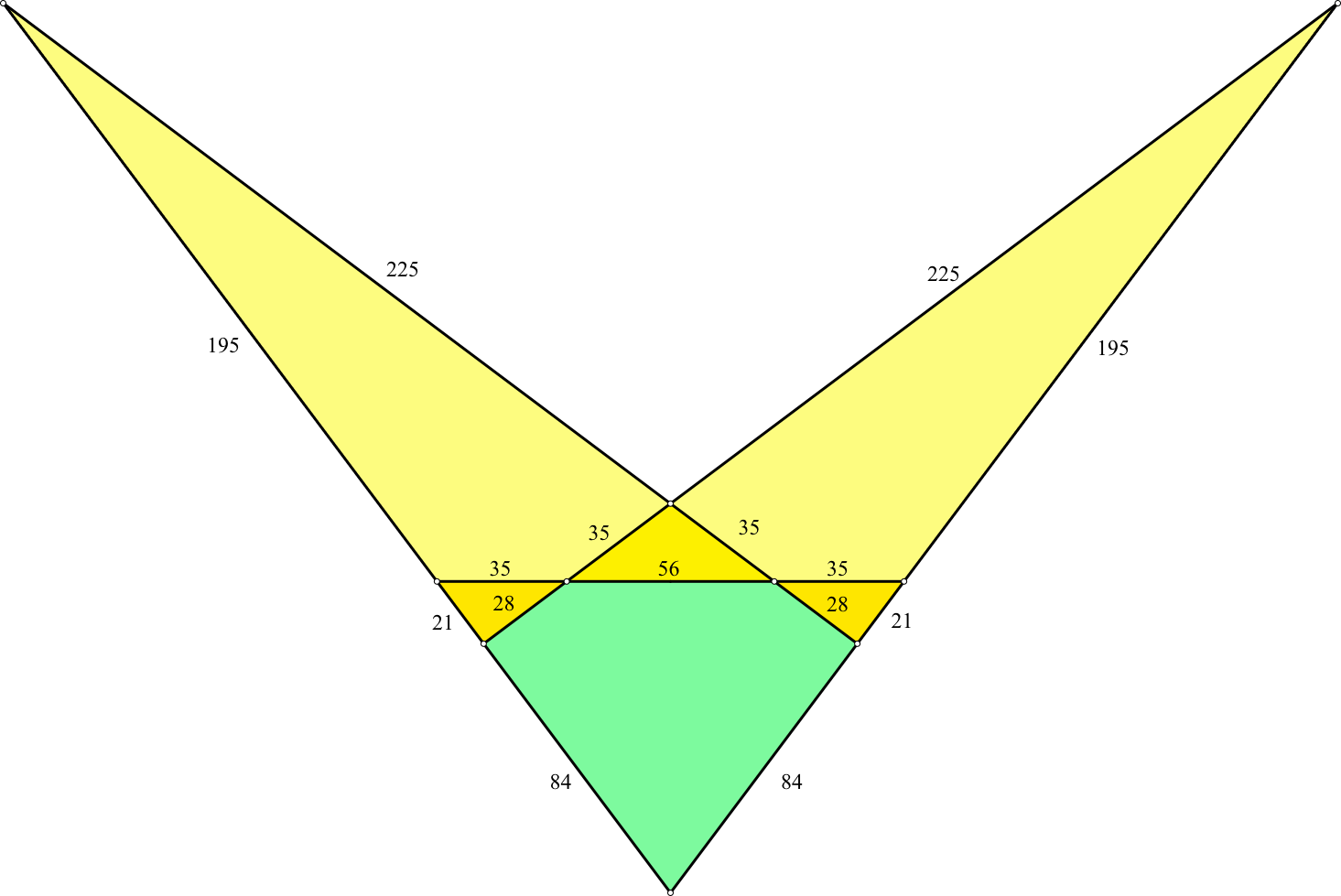
Abb. 6: Verwandte Konfiguration

Die Abbildung 7 zeigt eine weitere Lösung mit global ganzzahligen Teilverhältnissen. Die Lösung basiert auf dem pythagoreischen Dreieck mit dem Seitenverhältnis 5 : 12 : 13.

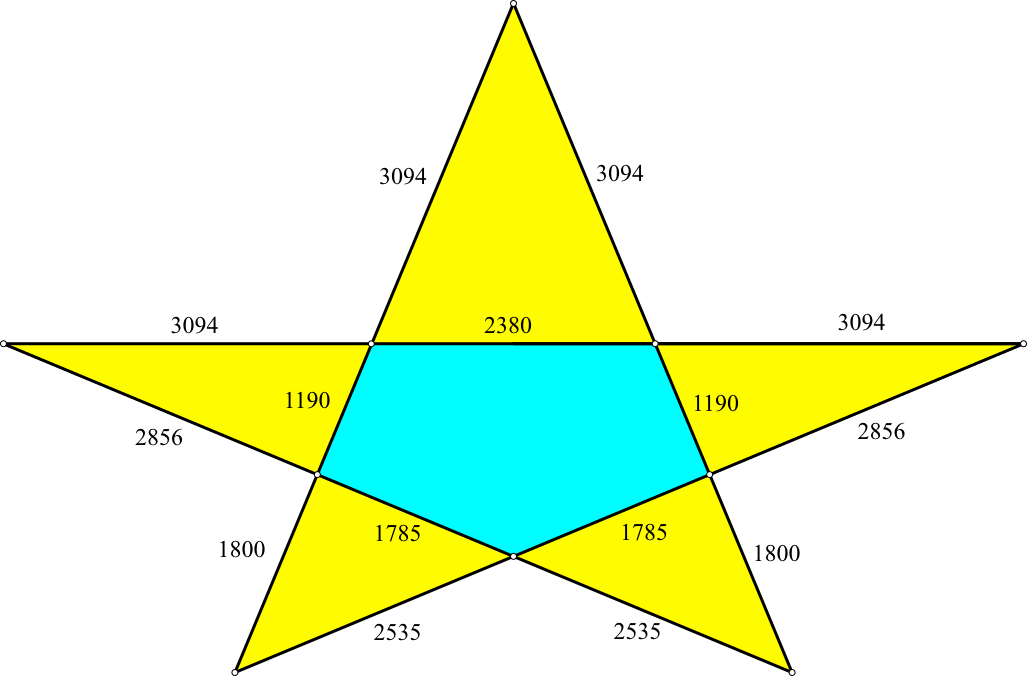
Abb. 7: Global ganzzahlige Teilverhältnisse

Der Autor weiß nicht, ob und allenfalls wie dies allgemein mit pythagoreischen Dreiecken funktioniert.

Weblinks

Hans Walser: Ganze Zahlen im gleichseitigen Dreieck

https://walser-h-m.ch/hans/Miniaturen/G/Ganze_Zahlen_im_gls_Dreieck/Ganze_Zahlen_im_gls_Dreieck.htm

Hans Walser. Pythagoreische 60°- und 120°-Dreiecke

https://walser-h-m.ch/hans/Miniaturen/P/Pyth-60-Dreiecke/Pyth-60-Dreiecke.htm