Hans Walser, [20231105]

Schließungsfigur

Idee und Anregung: Helmut Mallas, Flensburg

1 Worum es geht

Exemplarische Beispiele zu Schließungsfiguren mit gegebener Periodenlänge.

Bestandesaufnahme. Ohne Beweis

2 Beispiele

Mit n und k bezeichnen wir natürliche Zahlen. Weiter sei:

Wir arbeiten nun mit der Funktion:

Deren Funktionsgraf ist eine Hyperbel (in den Abbildungen rot) mit der y-Achse als der einen Asymptote und der Geraden y = p (in den Abbildungen zyan) als der anderen Asymptote.

Weiter verwenden wir die Gerade y = x (in den Abbildungen blau).

Im Folgenden wählen wir n = 15.

2.1 Beispiel 1

Wir wählen k = 1. Die Abbildung 1 zeigt die Hyperbel. Es ist p ≈ 1.956. Die blaue Gerade berührt die rote Hyperbel nicht.

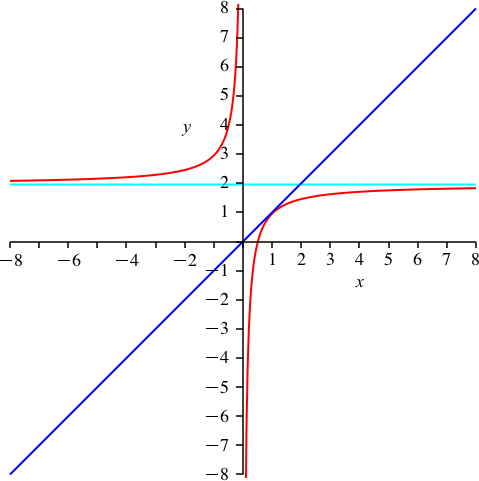
Abb. 1: Disposition

Nun wählen wir auf der Hyperbel einen beliebigen Startpunkt (rot-grün in Abb. 2). Von diesem Startpunkt aus fahren wir horizontal bis zur blauen Gerade. Von dort vertikal bis zur Hyperbel. Dann wieder horizontal bis zur blauen Gerade und vertikal zur Hyperbel. Und so weiter und so fort. Nach 15 Doppelschritten (15 mal waagrecht und 15 mal senkrecht) kommen wir zum Startpunkt zurück. Wir haben eine Schließungsfigur der Periodenlänge 15.

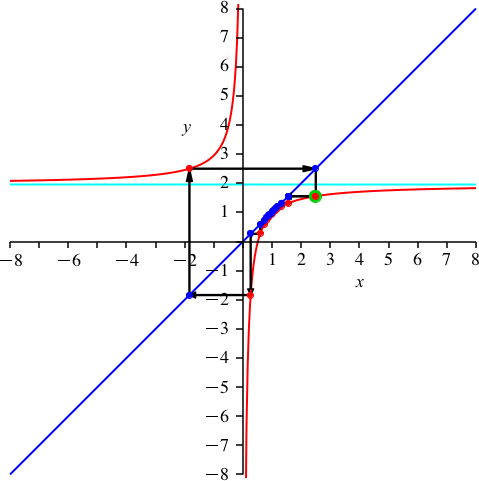
Abb. 2: Schließungsfigur der Periodenlänge 15

Auf dem oberen Hyperbelast haben wir einen roten Punkt, auf dem unteren Hyperbelast die restlichen 14 roten Punkte (den Startpunkt eingeschlossen). Weiter ist auf der blauen Geraden ein blauer Punkt vom Ursprung aus gesehen links unten. Die restlichen 14 blauen Punkte sind rechts oben.

Die Abbildung 3 illustriert, dass der Startpunkt beliebig gewählt werden darf.

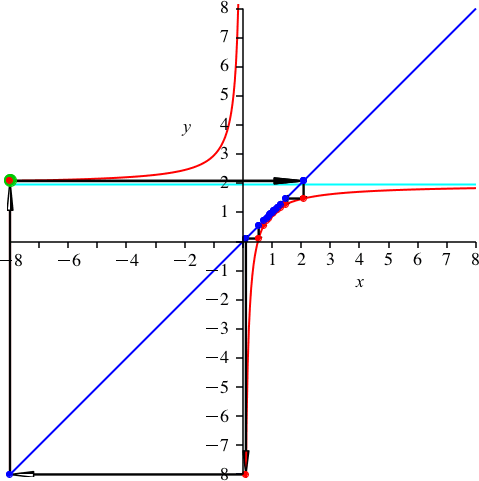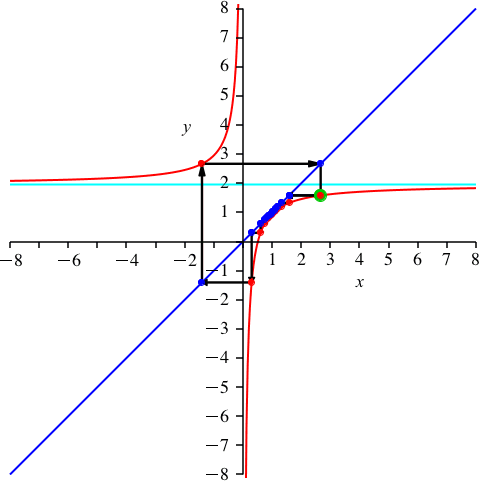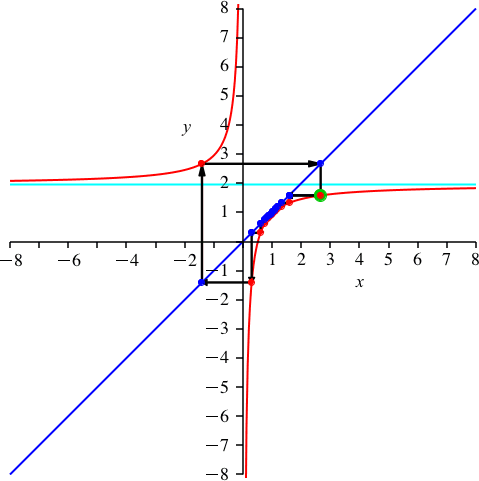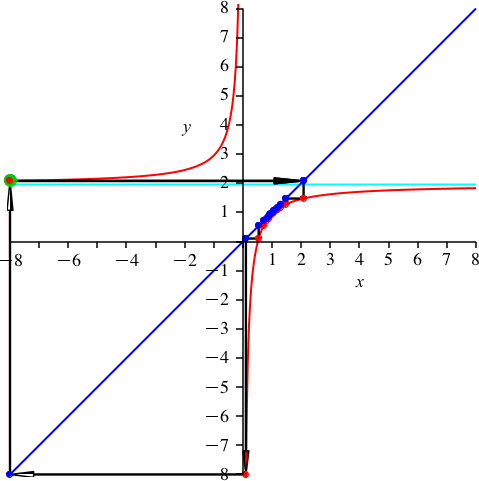
Abb. 3: Variation des Startpunktes

2.2 Beispiel 2

Nun wählen wir k = 2 (Abb. 4). Es ist p ≈ 1.827. Die Hyperbel rutscht also etwas nach unten.

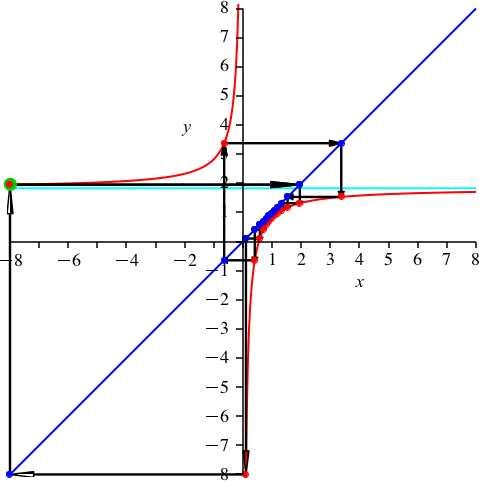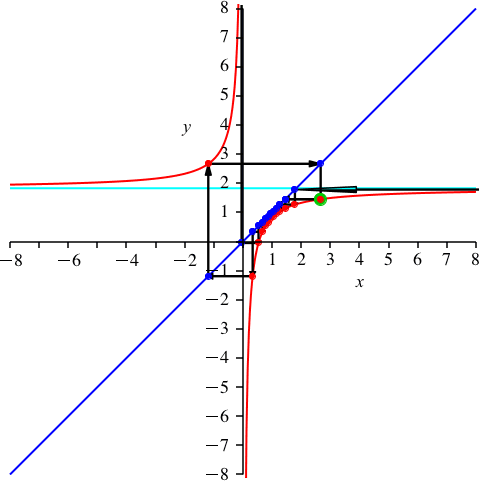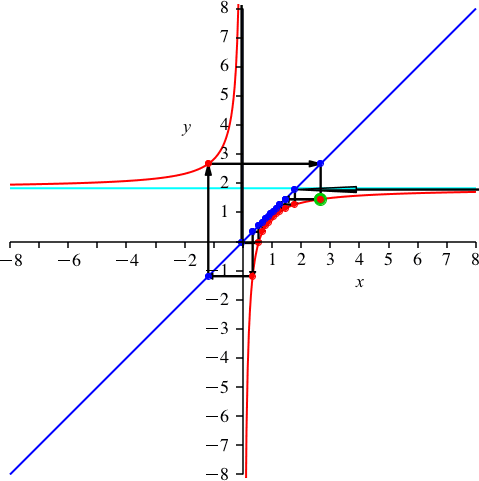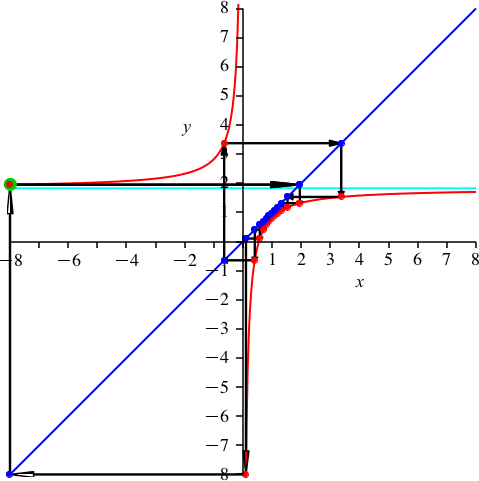
Abb. 4: k = 2

Wir haben nun zwei rote Punkte auf dem oberen Hyperbelast und 13 unten. Ebenso zwei blaue Punkte auf der blauen Geraden unterhalb des Ursprungs.

2.3 Beispiel 3

Wir wählen k = 3 (Abb. 5). Es ist p ≈ 1.618 (Goldener Schnitt). Wegen 15/3 = 5 haben wir scheinbar nur die Periodenlänge 5. In Wirklichkeit haben wir immer noch die Periodenlänge 15, aber 3 Durchgänge (jedenfalls kann man das so sehen).

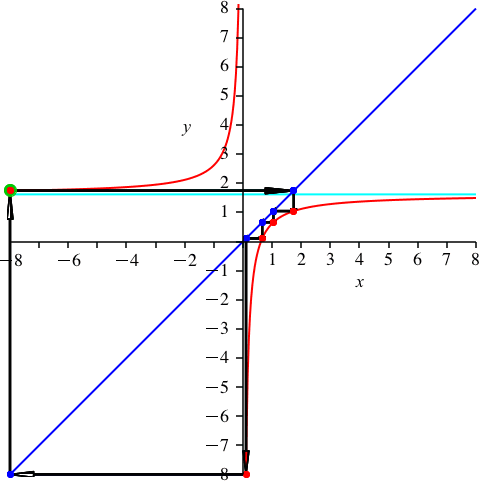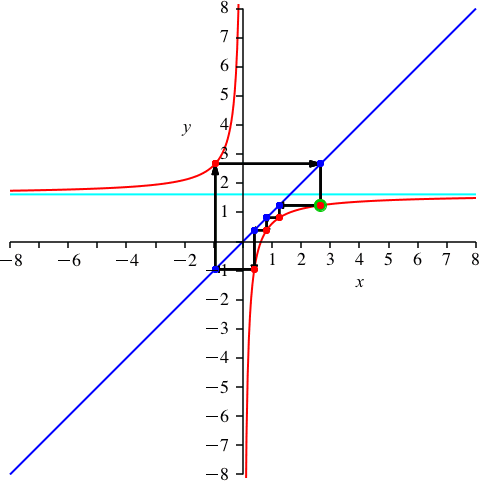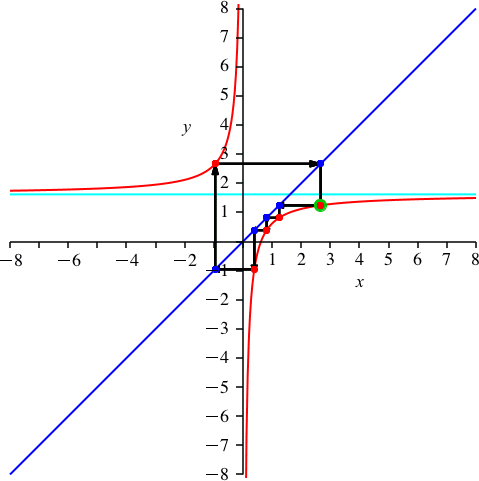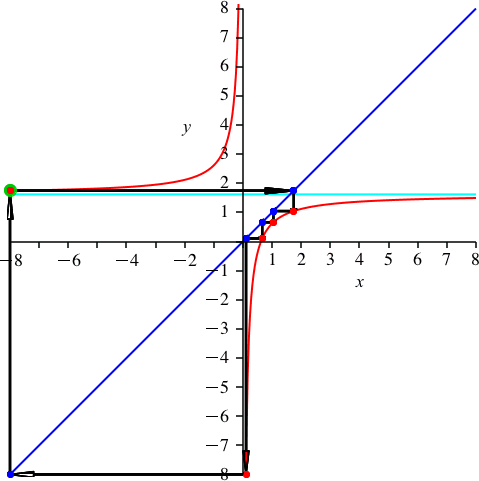
Abb. 5: n = 15 und k = 3

Auf dem oberen Hyperbelast haben wir einen dreifach zu zählenden roten Punkt.

2.4 Beispiel 4

Nun sei k = 4. Dies ist kein Teiler von n = 15. Daher sehen wir die volle Periodenlänge 15 (Abb. 6). Es ist p ≈ 1.338. Vier rote Punkte sind auf dem Hyperbelast links oben.

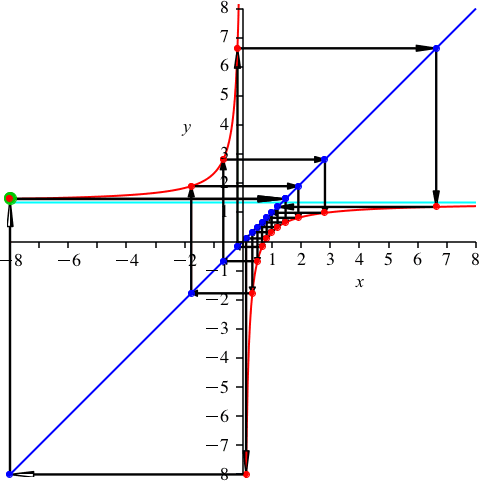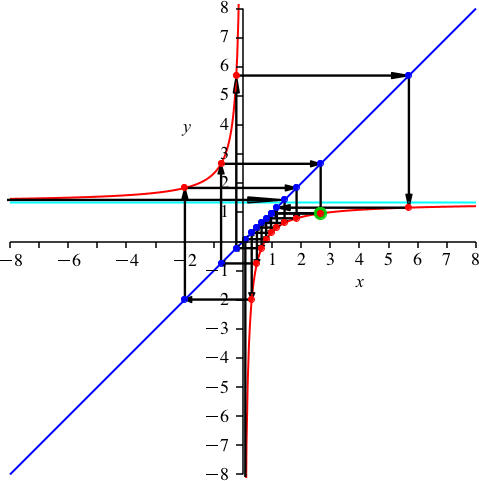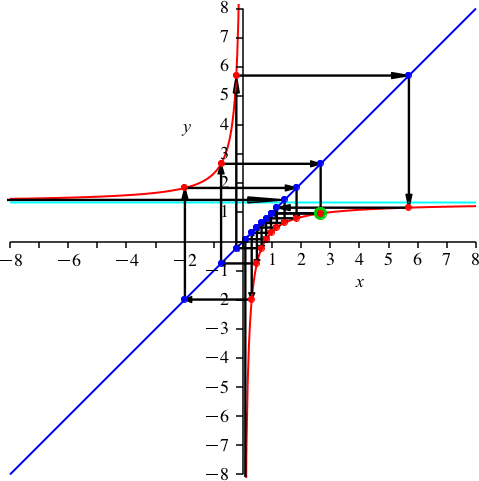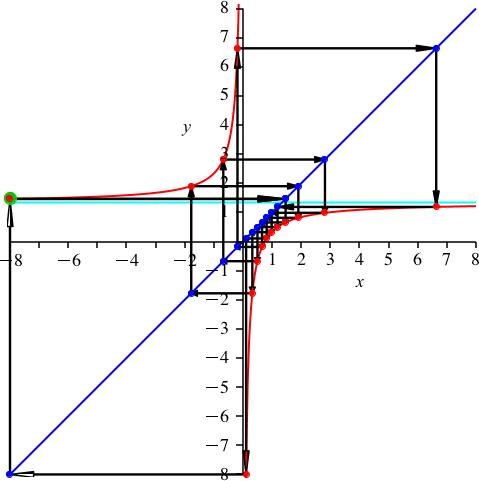
Abb. 6: k = 4

2.5 Beispiel 5

Mit k = 5 haben wir wieder einen Teiler von n = 15 (Abb. 7). Wir haben 5 Durchgänge und daher die scheinbare Periodenlänge 3. Es ist p = 1.

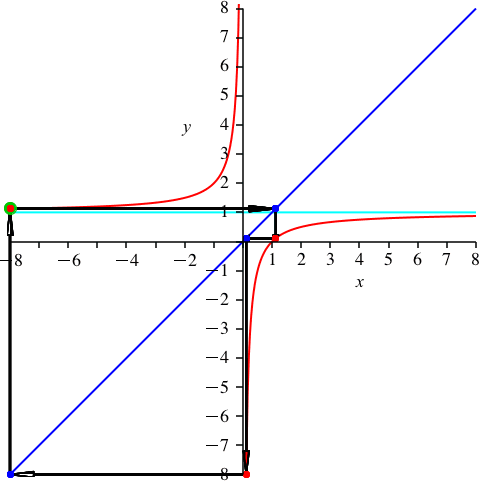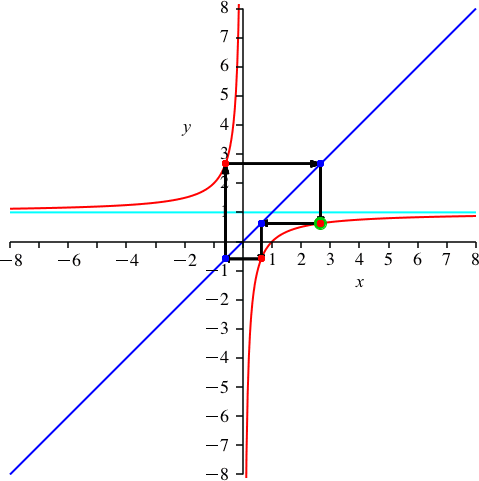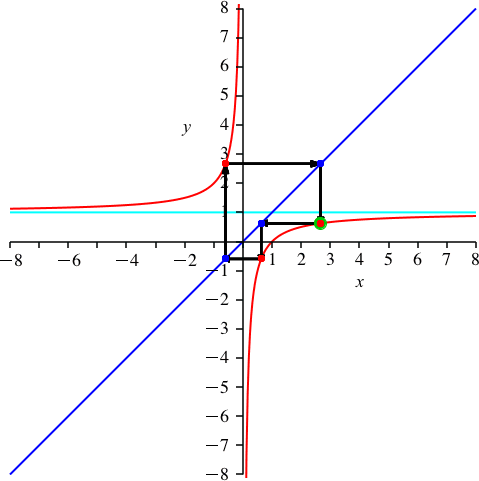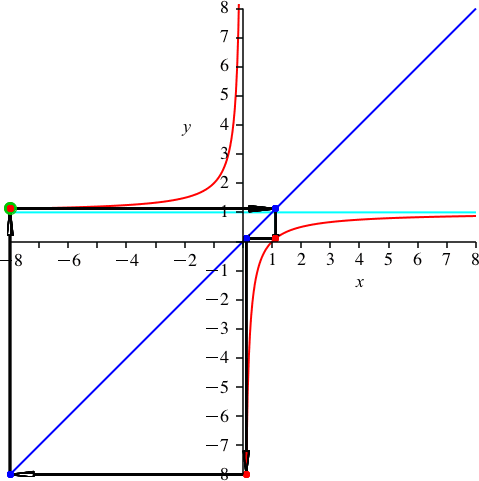
Abb. 7: k = 5

2.6 Beispiel 6

Die Zahlen k = 6 und n = 15 haben den gemeinsamen Teiler 3. Wir haben 3 Durchgänge und die scheinbare Periodenlänge 5 (Abb. 8). Auf dem oberen Hyperbelast haben wir 2 dreifach zu zählende rote Punkte. Es ist p ≈ 0.618 (Kehrwert des Goldenen Schnittes).

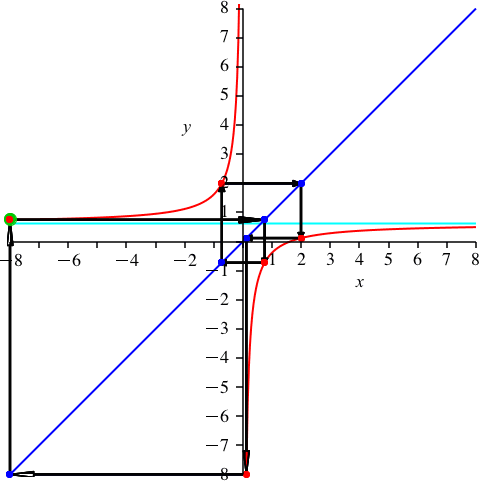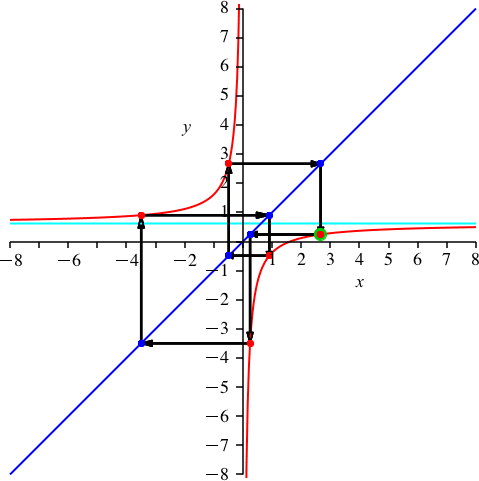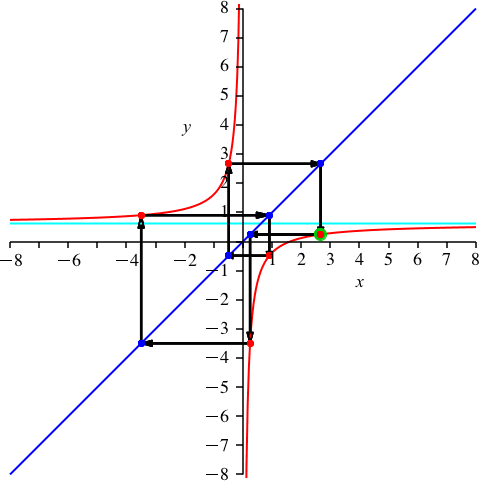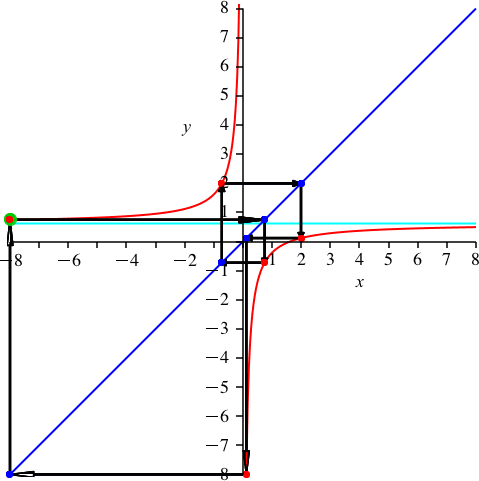
Abb. 8: k = 6

Man beachte die unterschiedliche Linienführung in den Abbildungen 5 und 8.

2.7 Beispiel 7

k = 7 ist teilerfremd zu n = 15 (Abb. 9). Es ist p ≈ 0.209. Wir haben 7 rote Punkte auf dem oberen Hyperbelast und 8 auf dem unteren.

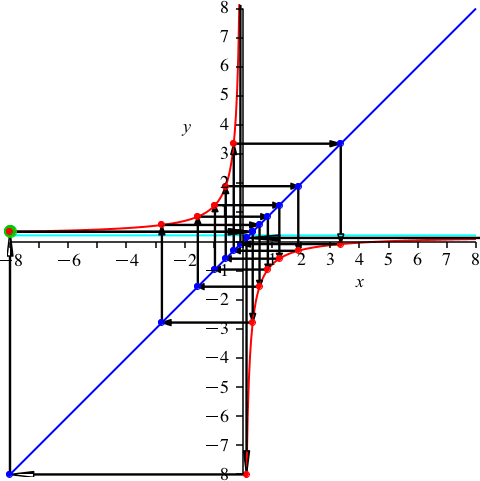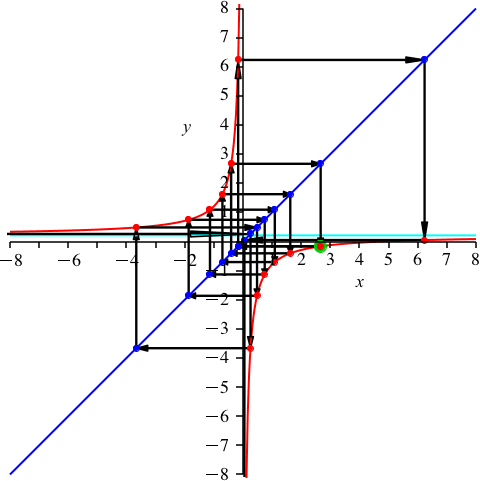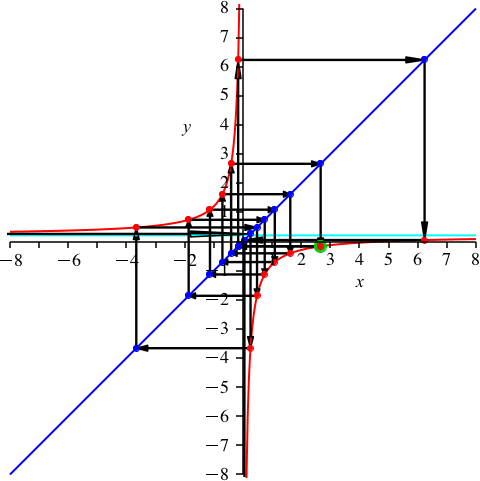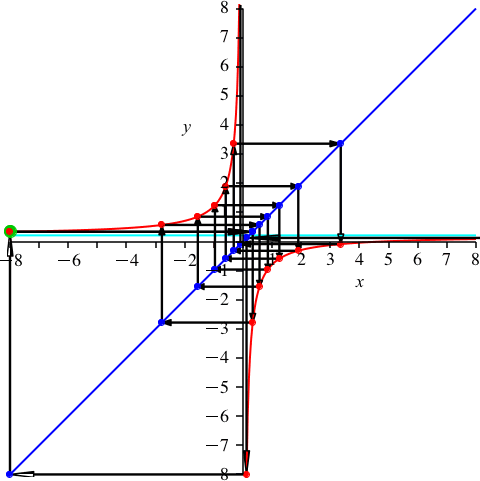
Abb. 9: k = 7

2.8 Beispiel 8

Mit k = 8 sind wir über der Mitte (Abb. 10). Es ist nun p ≈ –0.209. Dies ist die Gegenzahl im Vergleich zum Beispiel der Abbildung 9.

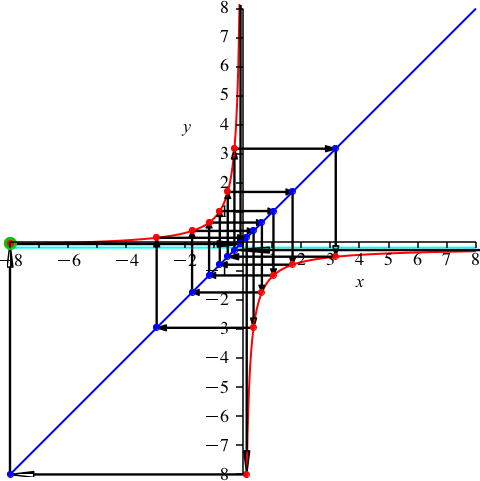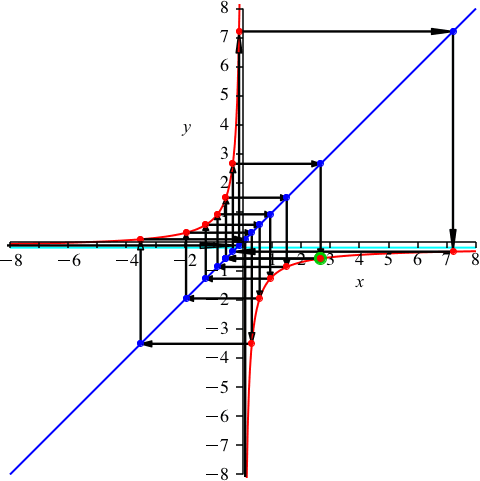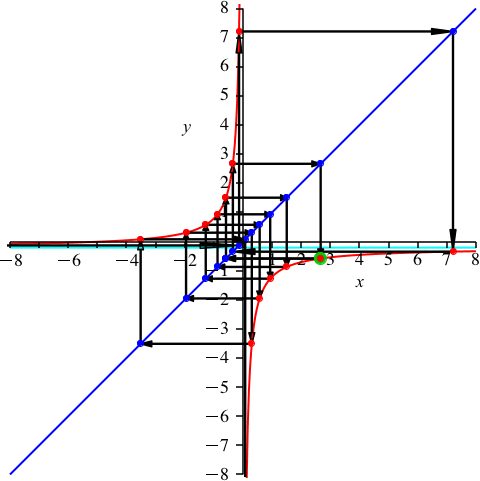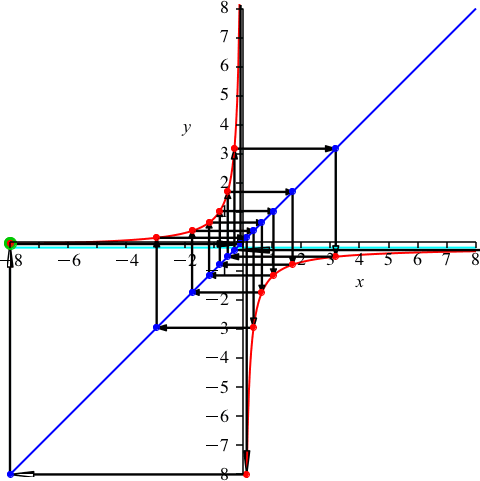
Abb. 10: k = 8

Um alle 8 roten Punkte auf der Hyperbelast oben links sichtbar zu machen, muss der Bildausschnitt vergrößert werden (Abb. 11). Rechts unten haben wir die restlichen 7 roten Punkte.

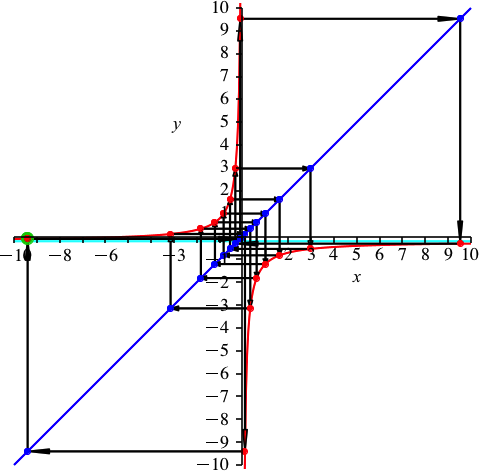
Abb. 11: Acht rote Punkte links oben

2.9 Beispiel 9

Mit k = 9 (Abb. 12) schließen wir die Liste ab, da es nun symmetrisch weitergeht. Es ist p ≈ –0.618 (negativer Kehrwert des Goldenen Schnittes).

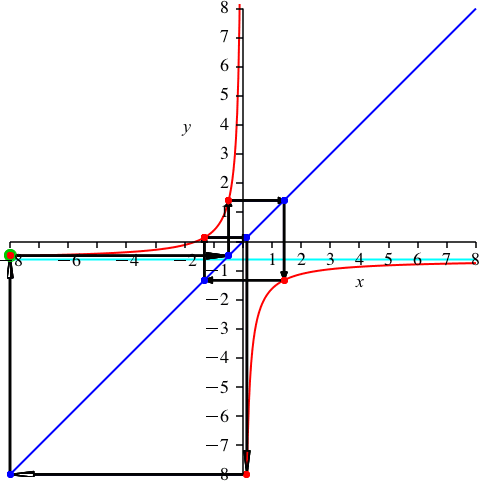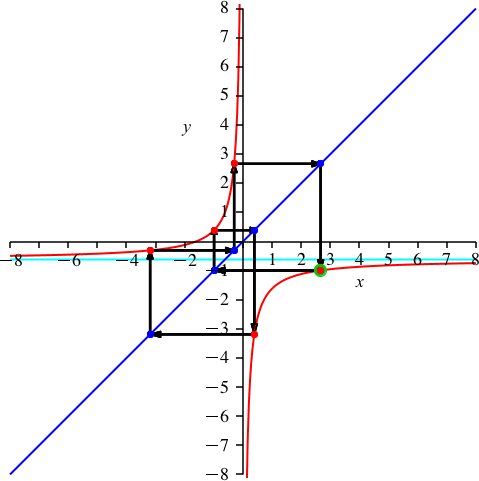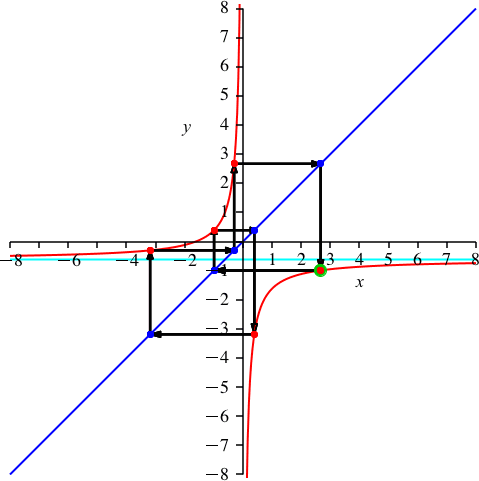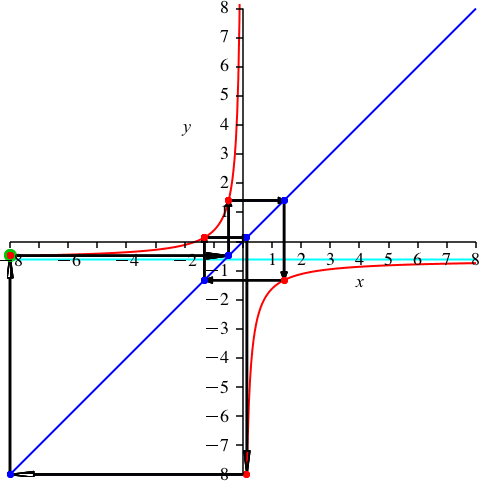
Abb. 12: k = 9

3 Hintergrund

Die Abbildungen sind Visualisierungen des folgenden Sachverhaltes: Zu beliebigem Startwert x₀ hat die Folge

die Periodenlänge n.
Die Tabelle 1 zeigt das Beispiel für n = 15, k = 3, x₀ = 2.

j	xj
0	2
1	1.118033988
2	0.7236067977
3	0.2360679773
4	–2.618033990
5	2
6	1.118033988
7	0.7236067977
8	0.2360679773
9	–2.618033990
10	2
11	1.118033988
12	0.7236067977
13	0.2360679773
14	–2.618033990
15	2

Tab. 1: Periodische Folge

Ohne Beweis.

Weblinks

Hans Walser: Schließungsfigur

https://walser-h-m.ch/hans/Miniaturen/S/Schliessungsfigur3/Schliessungsfigur3.html

Hans Walser: Schließungsfiguren

https://walser-h-m.ch/hans/Schliessungsfiguren/