Hans Walser, [20240202]

Schließungsfigur

1 Worum es geht

Im Kontext konfokaler Kegelschnitte entsteht ein Tangentenviereck.

2 Konstruktionsvorgang

Zu zwei Brennpunkten F₁ und F₂ und einem beliebigen Punkt A zeichnen wir die passende Ellipse und die passende Hyperbel.

Auf einem der beiden Kegelschnitte, zum Beispiel auf der Ellipse, wählen wir eine Startpunkt P₀. Die Folgepunkte P₁, P₂, ... zeichnen wir gemäß Abbildung 1. Nach vier Schritten schließt sich die Figur in P₄ = P₀. Das Viereck P₀P₁P₂P₃ ist ein Tangentenviereck. Nachweis mit Abstandseigenschaften von Ellipse und Hyperbel sowie eines Tangentenviereckes. Die Kegelschnitttangenten in den Eckpunkten des Viereckes P₀P₁P₂P₃ verlaufen durch den Inkreismittelpunkt. Dies ist eine Folge der Reflexionseigenschaften der Kegelschnitte.

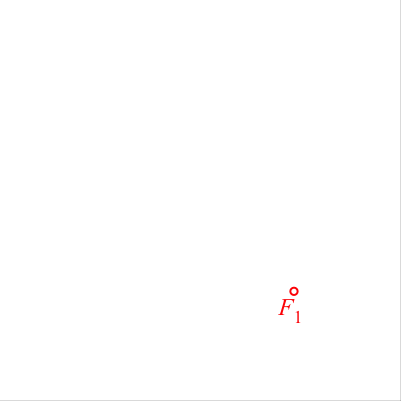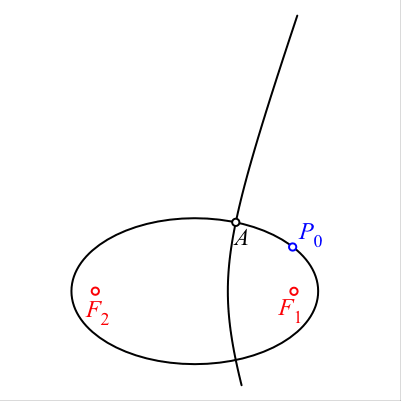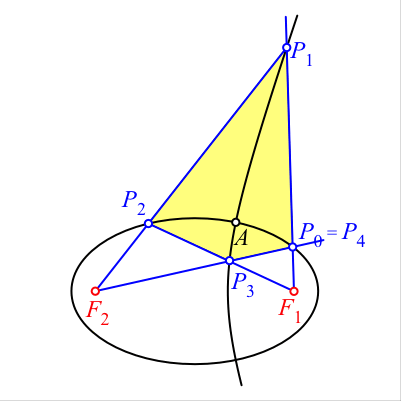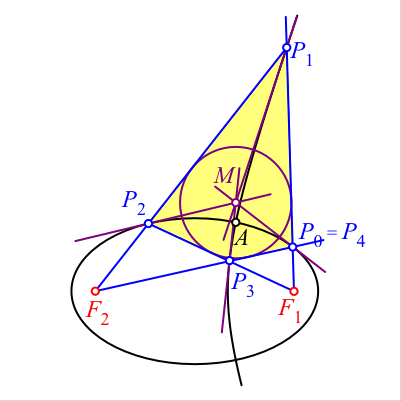
Abb. 1: Konstruktionsvorgang mit Beschriftung

Die Abbildung 2 zeigt den Konstruktionsvorgang ohne Beschriftung.

Abb. 2: Konstruktionsvorgang

Weblinks

Hans Walser: Tangentenviereck

https://walser-h-m.ch/hans/Miniaturen/T/Tangentenviereck2/Tangentenviereck2.html