Hans Walser, [20240425]

Schnittpunkt auf Hyperbel

1 Worum es geht

Parametrisierter Schnittpunkt im Dreieck. Hyperbel als Bahnkurve.

Experimentelle Befunde (dynamische Geometrie-Software)

2 Konstruktion

Wir beginnen mit einem beliebigen Dreieck und zeichnen in Kreissektoren mit gleichem Radius ein (Abb. 1). Den Radius bezeichnen wir mit t. Er ist der Parameter der Figur. Für t > 0 sollen die Kreissektoren ins Innere des Dreieckes schauen, für t < 0 nach außen (wie in Abb. 1).

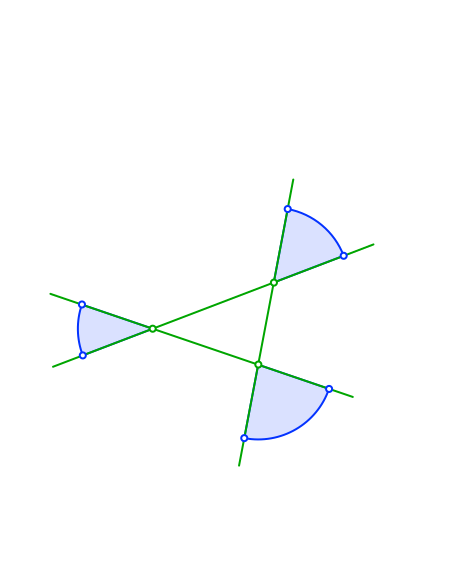
Abb. 1: Startdreieck mit Kreissektoren

Die Sektorsehnen verlängern wir zu einem Dreieck (magenta in Abb. 2)

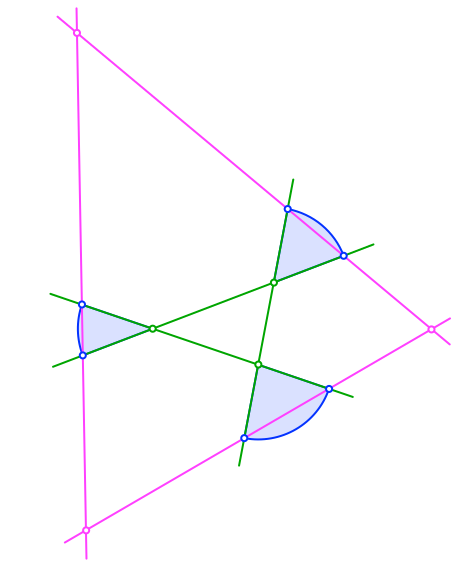
Abb. 2: Dreieck einpassen

Wir zeichnen ein weiteres Dreieck (orange in Abb. 3), dessen Seiten durch Bogenenden der Kreissektoren verlaufen.

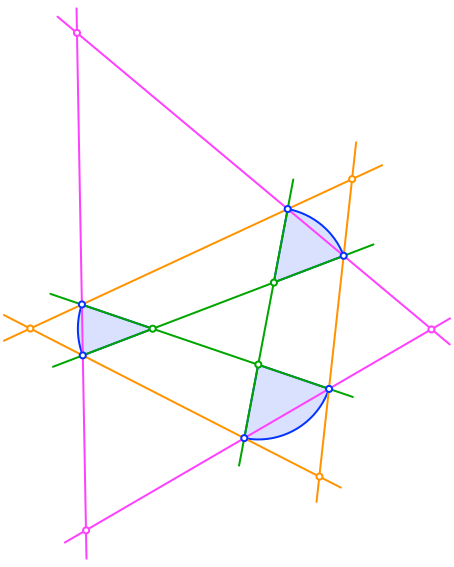
Abb. 3: Oranges Dreieck

Nun zeichnen wir eine Gerade (rot in Abb. 4) durch zwei diametrale Ecken des magenta Dreieck und des orangen Dreiecks. Diese Gerade verläuft auch durch eine Ecke des grünen Startdreiecks. Wir haben also drei kollineare Punkte.

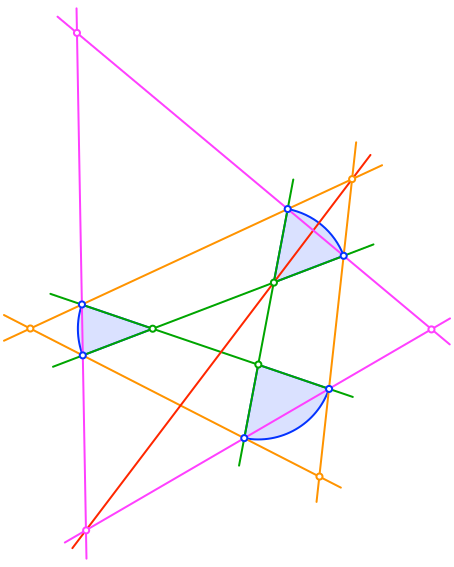
Abb. 4: Kollineare Punkte

Dies gilt auch für die beiden anderen Geraden durch diametrale Ecken (Abb. 5). Zudem haben die drei roten Geraden einen gemeinsamen Schnittpunkt.

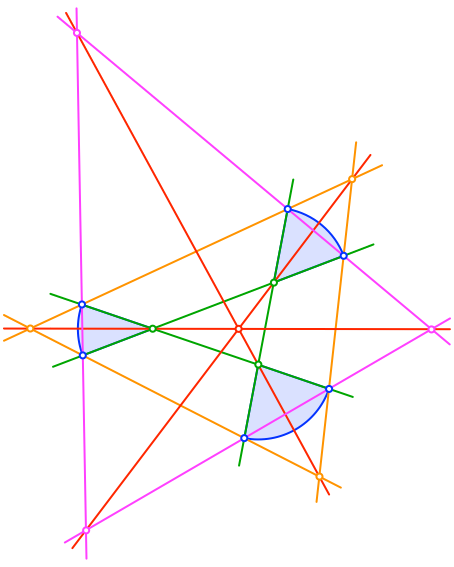
Abb. 5: Schnittpunkt

Die Abbildung 6 zeigt die Situation bei Variation des Kreissektor-Radius.

Abb. 6: Variation des Kreissektor-Radius

3 Sonderfälle

Für t → 0 streben die magenta Geraden streben gegen die äußeren Winkelhalbierenden des Dreiecks. Die orangen Geraden streben gegen die Seiten des grünen Startdreiecks. Die roten Geraden streben gegen die Winkelhalbierenden des Dreiecks und damit der Schnittpunkt gegen den Inkreismittelpunkt. Die Abbildung 7 zeigt die Situation für t = 0.01.

Abb. 7: Inkreismittelpunkt

Für t = ½ (a + b + c) (halber Umfang des Dreieckes) sind die roten Geraden rechtwinklig zu den Dreiecksseiten. Der Schnittpunkt ist daher der Höhenschnittpunkt (Abb. 8). (Wir können also die Höhen konstruieren, ohne Lote fällen zu müssen).

Abb. 8: Höhen und Höhenschnittpunkt

In dieser Situation sind die Bogenenden der Kreissektoren die Berührungspunkte der Ankreise an die verlängerten Dreieckseiten(Abb. 9).

Abb. 9: Ankreise

4 Hyperbel als Bahnkurve

Wir zeichnen die Hyperbel, welche durch die drei Eckpunkte des Dreiecks sowie seinen Inkreismittelpunkt und seinen Höhenschnittpunkt bestimmt ist (Abb. 10). Diese Hyperbel ist die Bahnkurve des Schnittpunktes (Abb. 11).

Abb. 10: Hyperbel

Bemerkung: Es handelt sich nicht um die Kiepert-Hyperbel, welche durch die drei Eckpunkte, den Schwerpunkt und den Höhenschnittpunkt bestimmt ist.

Abb. 11: Bahnkurve

Weblinks

Hans Walser: Schnittpunkt

https://walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt8/Schnittpunkt8.html

Hans Walser: Schnittpunkte

https://walser-h-m.ch/hans/Schnittpunkte/