Hans Walser, [20240506]
Spezielle pythagoreische Dreiecke
1 Worum es geht
Pythagoreische Dreiecke, deren Hypotenuse c um 2 länger ist als die Kathete a.
2 Beispiele
Beim pythagoreischen Dreieck mit den Seitenlängen 3, 4, 5 (ägyptisches Dreieck) ist die Hypotenuse c um 2 länger als die Kathete a.
Beim pythagoreischen Dreieck mit den Seitenlängen 8, 6, 10 (verdoppeltes ägyptisches Dreieck, vertauschte Reihenfolge) ist die Hypotenuse c um 2 länger als die Kathete a.
3 Problemstellung
Gesucht sind alle pythagoreischen Dreiecke mit c = a + 2 (in der üblichen Notation).
4 Bearbeitung
Aus der üblichen Parametrisierung der pythagoreischen Dreiecke
a = u2 – v2
b = 2uv
c = u2 + v2
liefert die Bedingung c = a + 2:
u2 + v2 = u2
– v2 + 2
2v2 = 2
v = ±1
Wegen v > 0 kommt nur +1 in Frage. Somit ist:
v = 1
Die Tabelle 1 gibt die ersten Werte. Die Tabelle ist überschaubar.
|
u |
v |
a |
b |
c |
|
1 |
1 |
0 |
2 |
2 |
|
2 |
1 |
3 |
4 |
5 |
|
3 |
1 |
8 |
6 |
10 |
|
4 |
1 |
15 |
8 |
17 |
|
5 |
1 |
24 |
10 |
26 |
|
6 |
1 |
35 |
12 |
37 |
|
7 |
1 |
48 |
14 |
50 |
|
8 |
1 |
63 |
16 |
65 |
|
9 |
1 |
80 |
18 |
82 |
|
10 |
1 |
99 |
20 |
101 |
Tab. 1: Erste Beispiele
5 Visualisierungen
Die Abbildung 1 zeigt die ersten 10 Dreiecke.

Abb. 1: Die ersten 10 Dreiecke
Die Spitzen liegen auf einer liegenden quadratischen Parabel (Abb. 2). Die Parabel hat ihren Brennpunkt in der gemeinsamen Ecke der Dreiecke links unten.
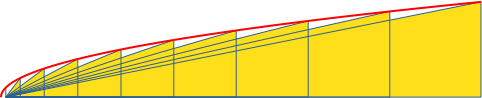
Abb. 2: Liegende Parabel
Die Abbildung 3 zeigt die ersten 50 Beispiele, wobei die Hypotenusen auf gleiche Länge normiert sind. Die Spitzen bewegen sich daher auf einem Viertelkreis.

Abb. 3: Normierte Hypotenusen
Weblinks
Hans Walser: Spezielle pythagoreische Dreiecke