Hans Walser, [20240131]

Tangententrapez

Anregung: Helmut Mallas, Flensburg

1 Worum es geht

Tangententrapez und Parabeln

2 Tangententrapez gegeben

Wir beginnen mit einem Trapez, das einen Inkreis hat, also einem Tangententrapez (Abb. 1).

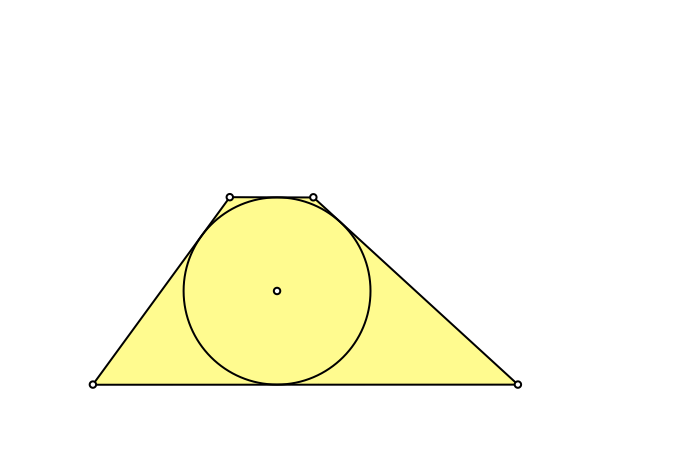
Abb. 1: Tangententrapez

2.1 Brennpunkt und Symmetrieachse

Durch den Schnittpunkt der beiden Schrägseiten zeichnen wir eine Parallele zu den Parallelseiten (Abb. 2). Den Schnittpunkt werden wir als Brennpunkt und die Parallele als Symmetrieachse einer noch zu bestimmenden Parabel verwenden.

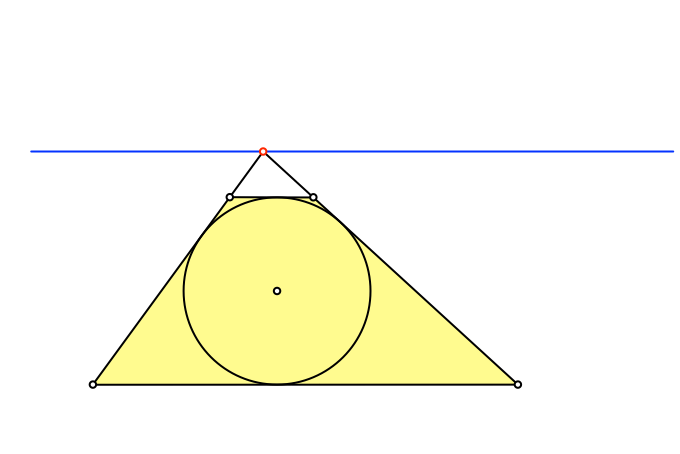
Abb. 2: Brennpunkt und Symmetrieachse

2.2 Parabel

Nun ist es so, dass es zu einem beliebigen Punkt genau eine nach rechts offene Parabel gibt, welche den gegebenen Brennpunkt und die gegebene Symmetrieachse hat. Konstruktion mit Hilfe der Leitlinie. (Es gibt eine zweite, nach links offene Parabel, welche ebenfalls durch den beliebigen Punkt verläuft).

Wir zeichnen nun die nach rechts offene Parabel, welche durch die linke obere Ecke des Tangententrapezes verläuft (Abb. 3).

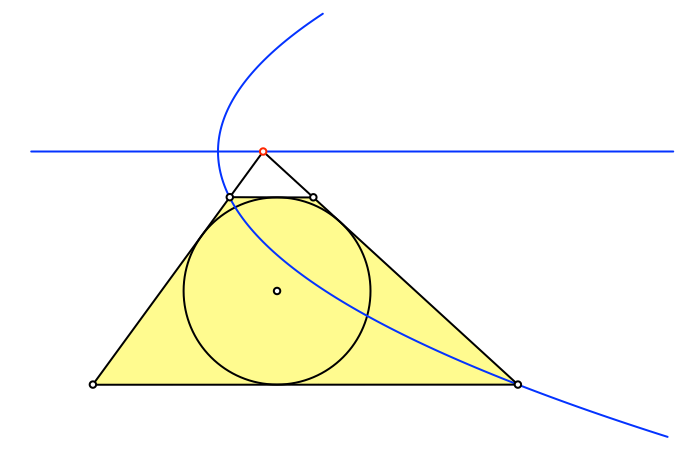
Abb. 3: Parabel

Der Gag ist nun, dass diese Parabel auch durch die rechte untere Ecke des Tangententrapezes verläuft. Beweis mit Abstandseigenschaften. (Die zweite, nach links offene Parabel durch die linke obere Ecke des Tangententrapezes verläuft aber nicht durch eine weitere Ecke des Tangententrapezes).

2.3 Zweite Parabel

Wir können aber eine zweite, nach links offene Parabel zeichnen, welche durch die rechte obere Ecke des Tangententrapezes verläuft (Abb. 4).

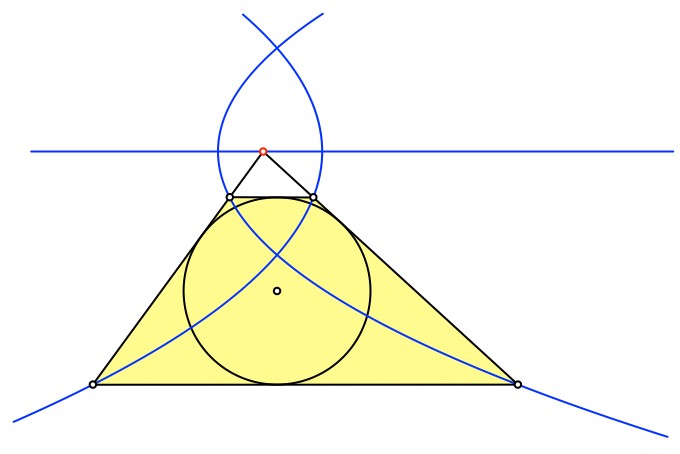
Abb. 4: Zweite Parabel

Diese Parabel verläuft durch die linke untere Ecke des Tangententrapezes.

Wir haben also zwei parabolische Diagonalen. Diese schneiden sich senkrecht (konfokale Parabeln).

2.4 Parabeltangenten

Die Parabeltangenten in den Eckpunkten des Tangententrapezes verlaufen durch den Inkreismittelpunkt (Abb. 5). Folge der Reflexionseigenschaft der Parabeln.

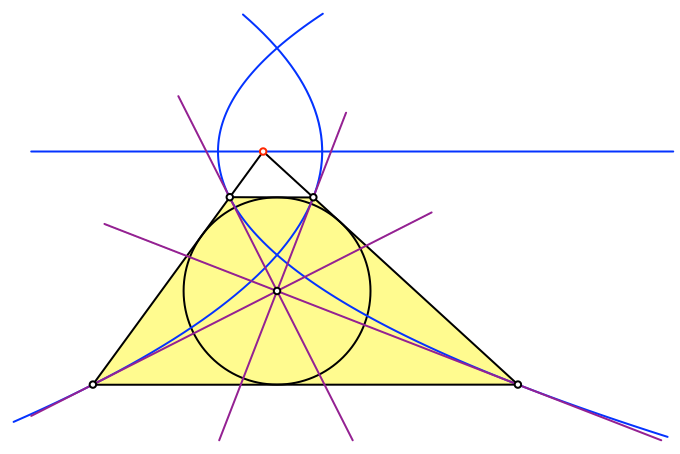
Abb. 5: Inkreismittelpunkt

3 Umkehrung

Wir beginnen mit einer Parabel mit Brennpunkt und Symmetrieachse (Abb. 6). Zur Abwechslung einmal schief.

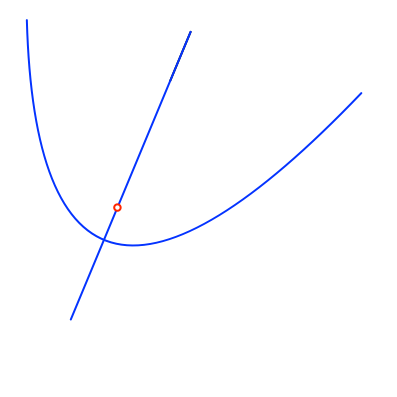
Abb. 6: Parabel mit Brennpunkt und Symmetrieachse

3.1 Zwei beliebige Punkte auf der Parabel

Auf der Parabel wählen wir zwei beliebige Punkte (Abb. 7).

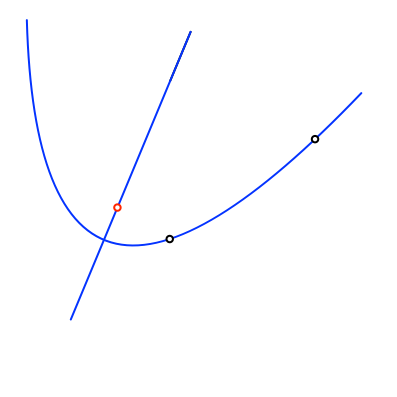
Abb. 7: Zwei Punkte auf der Parabel

3.2 Parallele Geraden

Durch die beiden Punkte legen wir zur Symmetrieachse parallele Geraden (Abb. 8).

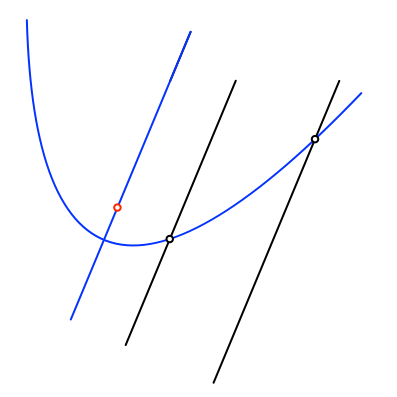
Abb. 8: Parallele Geraden

3.3 Verbindung mit Brennpunkt

Weiter verbinden wir die beiden Punkte mit dem Brennpunkt (Abb. 9).

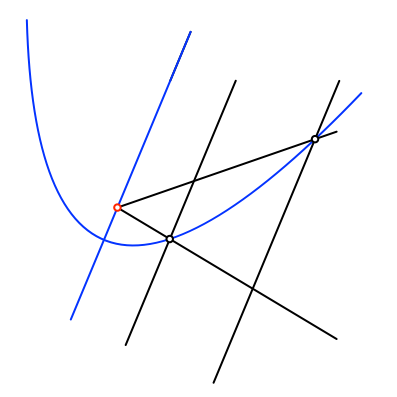
Abb. 9: Verbindung mit Brennpunkt

3.4 Tangententrapez

So entsteht ein Trapez (Abb. 10). Es hat einen Inkreis, ist also ein Tangententrapez.

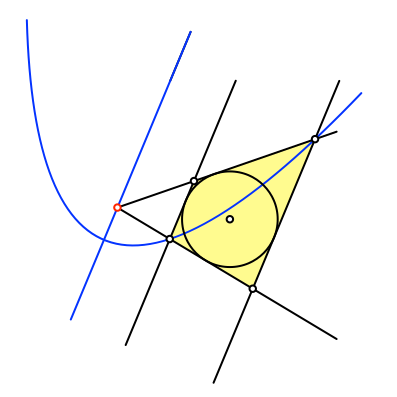
Abb. 10: Tangententrapez

3.5 Parabeltangenten

Die Parabeltangenten in den beiden Punkten verlaufen durch den Inkreismittelpunkt (Abb. 11).

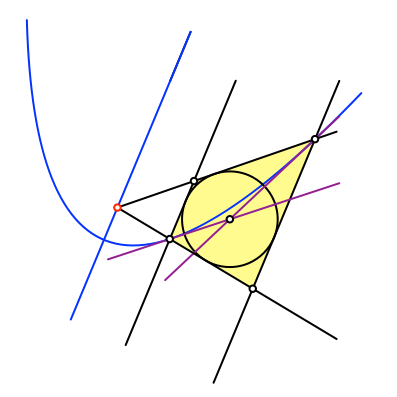
Abb. 11: Inkreismittelpunkt

Weblinks

Hans Walser: Tangentenviereck

https://walser-h-m.ch/hans/Miniaturen/T/Tangentenviereck2/Tangentenviereck2.html