Hans Walser, [20240225]
Tetraeder im Würfel
1 Worum es geht
Von den acht Eckpunkten eines Würfels werden vier ausgewählt. Diese bilden ein in der Regel nicht regelmäßiges Tetraeder.
Wie viele Möglichkeiten gibt es?
Eine Fleißarbeit
2 Kombinatorik
Es gibt binomial(8, 4) = 70 Möglichkeiten.
3 Beispiele
3.1 Seite
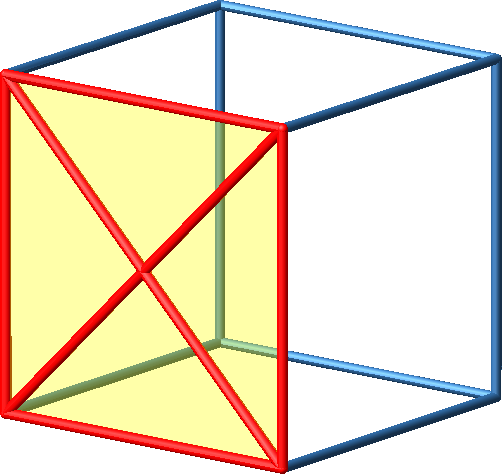
Abb. 1a: Seite
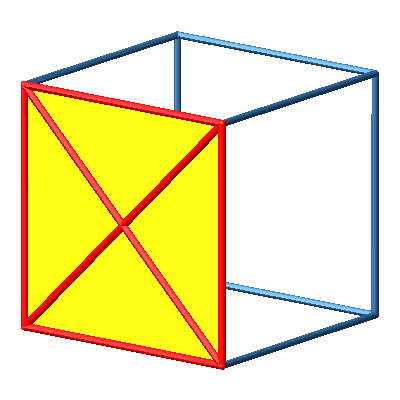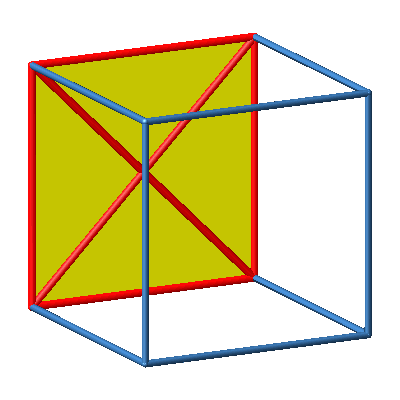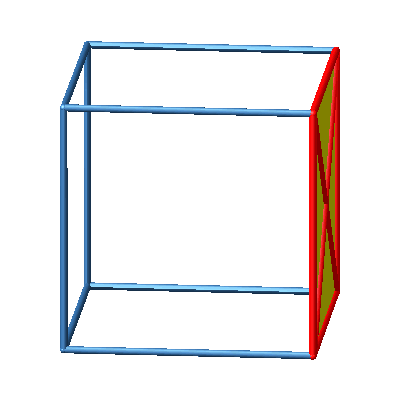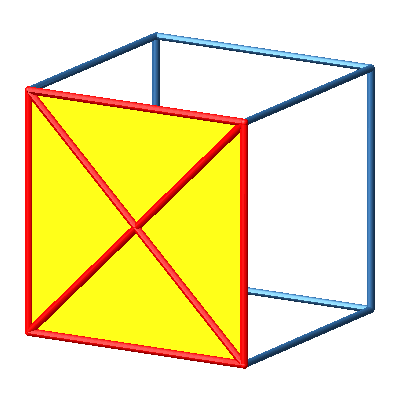
Abb. 1b: Seite
3.2 Diagonalrechteck
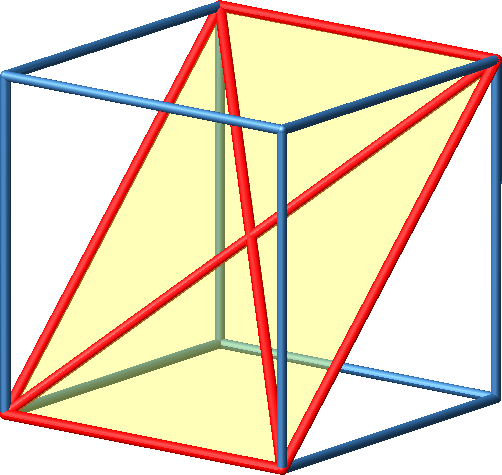
Abb. 2a: Diagonalrechteck
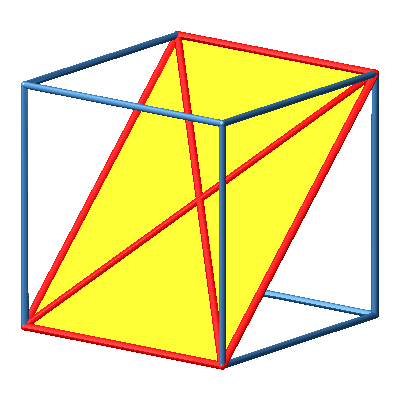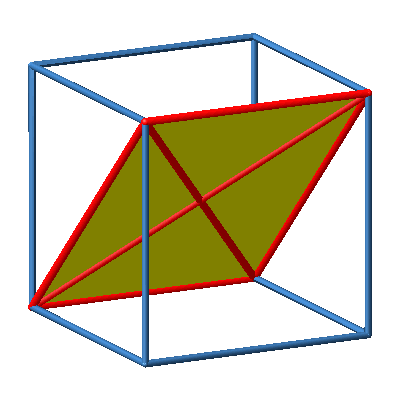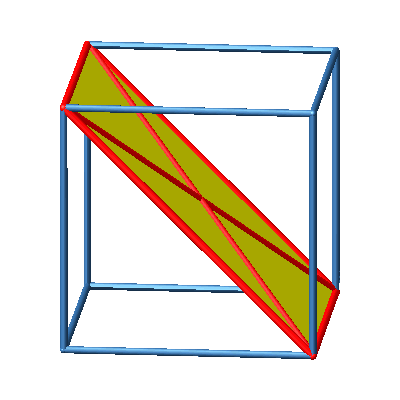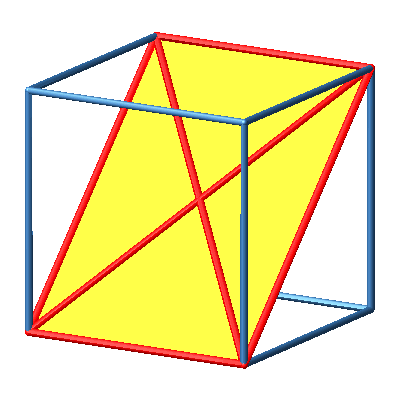
Abb. 2b: Diagonalrechteck
3.3 Regelmäßiges Tetraeder
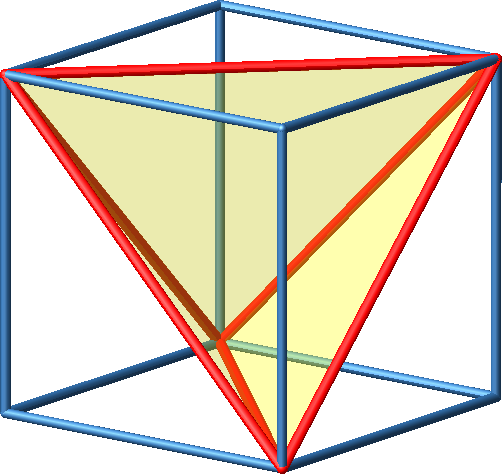
Abb. 3a: Regelmäßiges Tetraeder
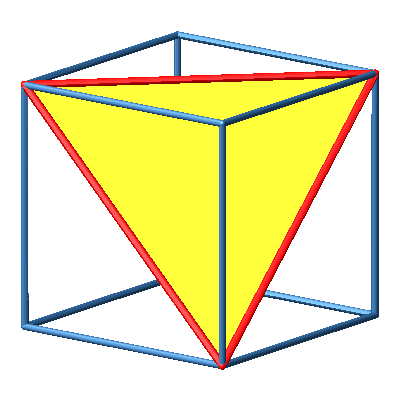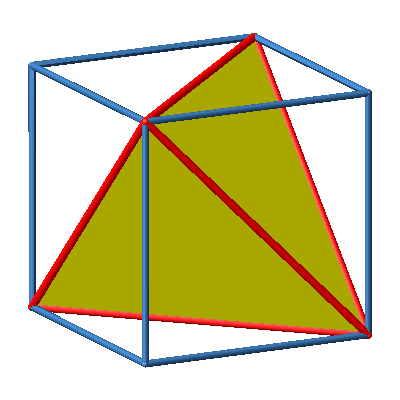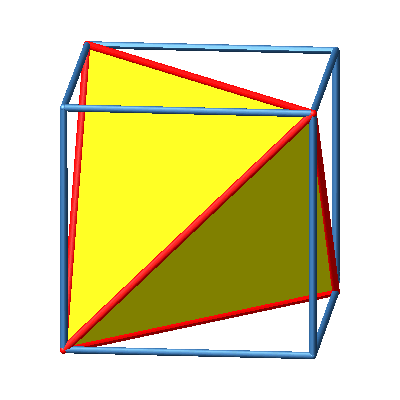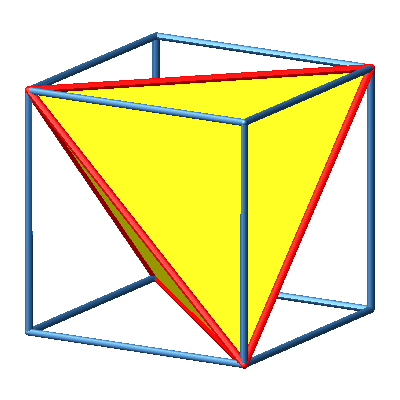
Abb. 3b: Regelmäßiges Tetraeder
3.4 Ecke
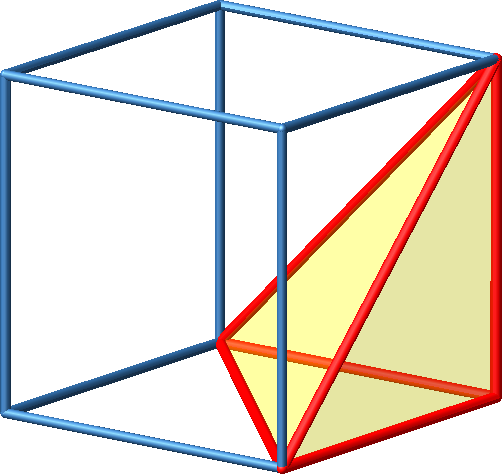
Abb. 4a: Ecke
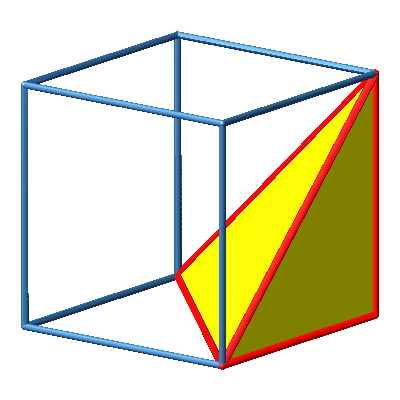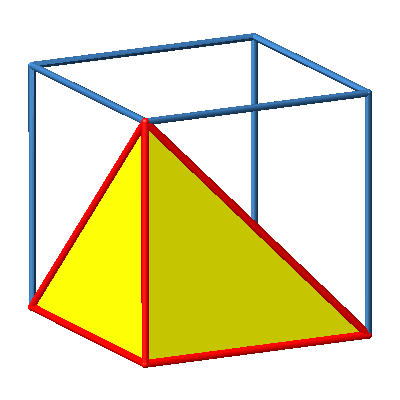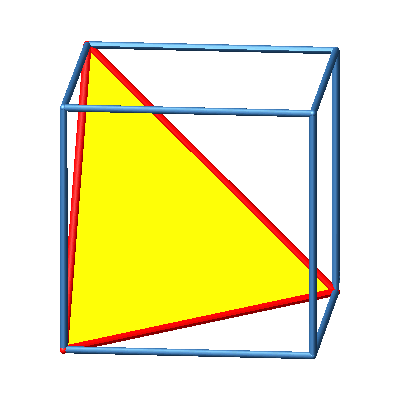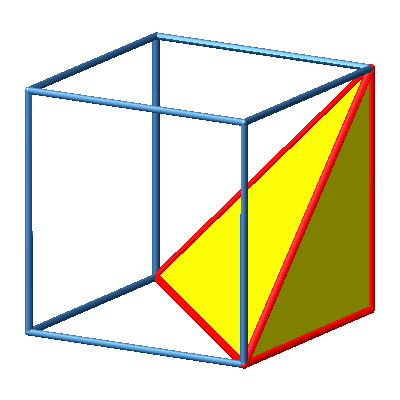
Abb. 4b: Ecke
3.5 Orthoschem rechts
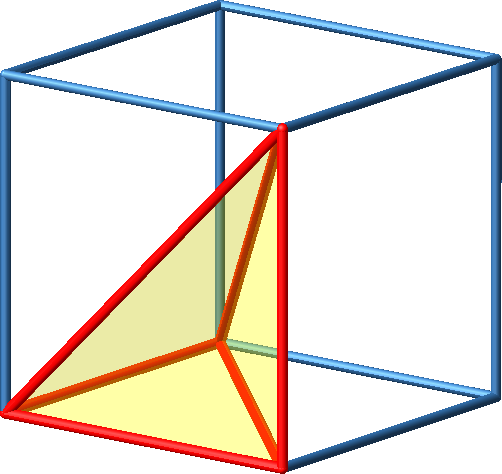
Abb. 5a: Orthoschem rechts
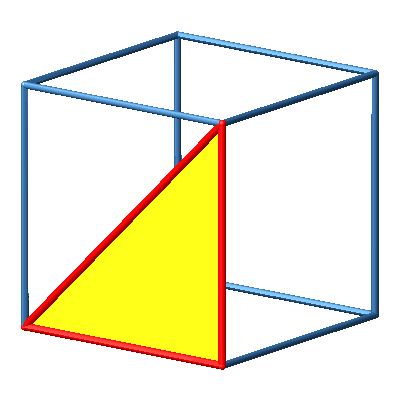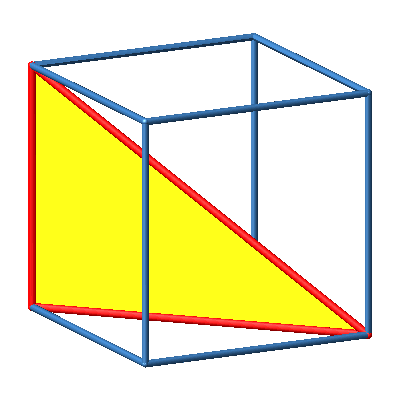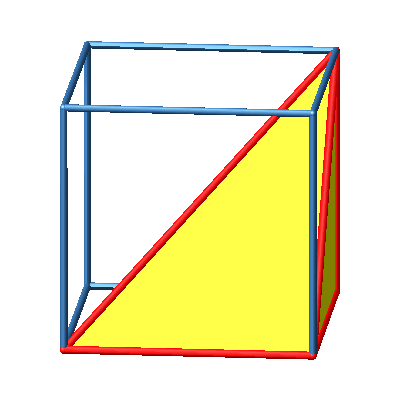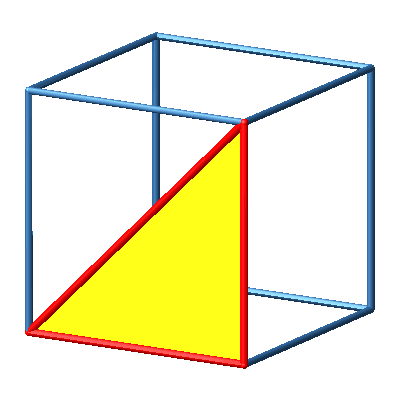
Abb. 5b: Orthoschem rechts
3.6 Orthoschem links
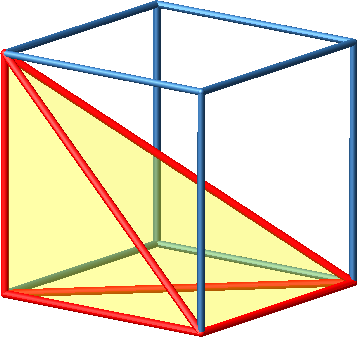
Abb. 6a: Orthoschem links
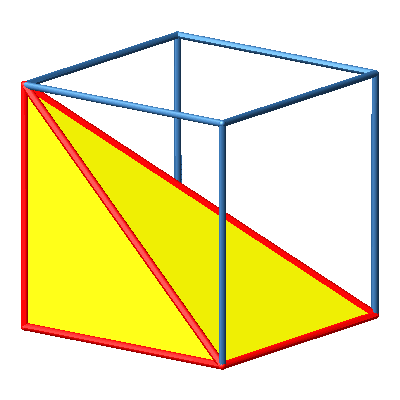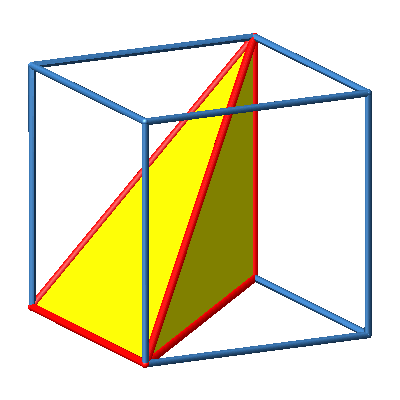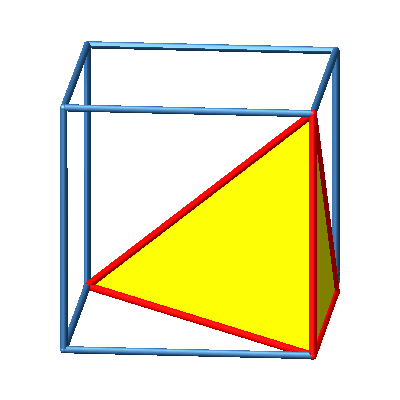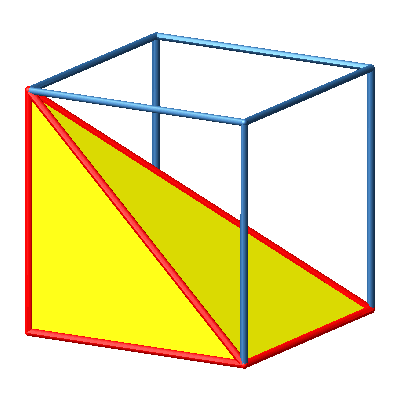
Abb. 6b: Orthoschem links
3.7 Schiefe Pyramide
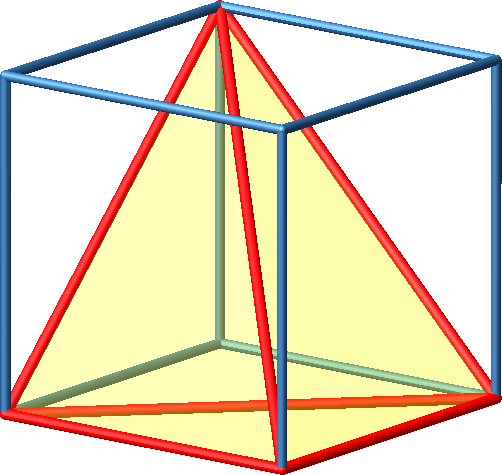
Abb. 7a: Schiefe Pyramide
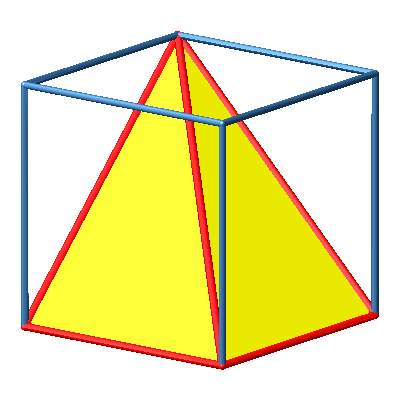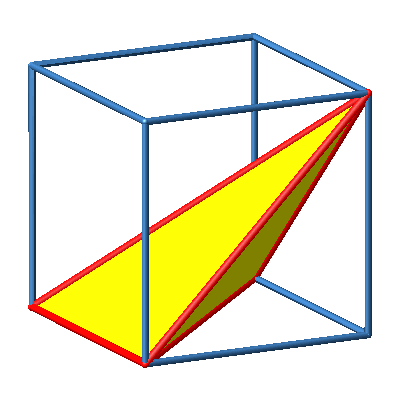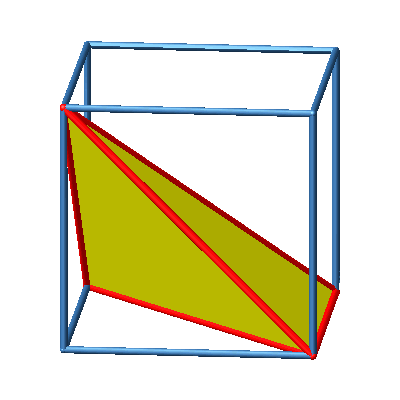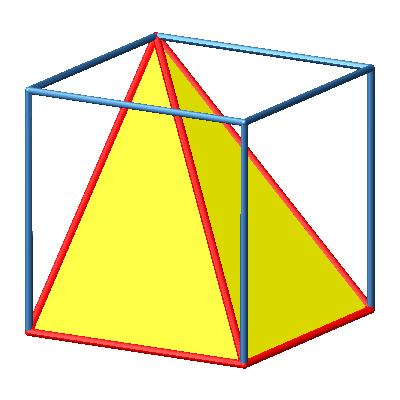
Abb. 7b: Schiefe Pyramide
4 Übersicht
|
Name |
Anzahl |
Zählweise |
Anzahl Kanten der Länge |
Volumen |
||
|
1 |
√2 |
√3 |
||||
|
Seite |
6 |
|
4 |
2 |
|
0 |
|
Diagonalrechteck |
6 |
|
2 |
2 |
2 |
0 |
|
Regelmäßiges Tetraeder |
2 |
|
|
6 |
|
1/3 |
|
Ecke |
8 |
1 pro Würfelecke |
3 |
3 |
|
1/6 |
|
Orthoschem rechts |
12 |
1 pro Würfelkante |
3 |
2 |
1 |
1/6 |
|
Orthoschem links |
12 |
1 pro Würfelkante |
3 |
2 |
1 |
1/6 |
|
Schiefe Pyramide |
24 |
4 pro Seitenfläche |
2 |
3 |
1 |
1/6 |
|
total |
70 |
|
|
|
|
|
Tab. 1: Übersicht
Weblink
Hans Walser: Tetraeder im Würfel
https://walser-h-m.ch/hans/Miniaturen/T/Tetraeder_im_Wuerfel/Tetraeder_im_Wuerfel.htm