1 Konstruktion

Wir beginnen mit der Einheitskugel (Abb. 1).

Abb. 1: Einheitskugel

Nun strecken wir eine kongruente, aber grüne Kugel in der x-Richtung mit dem Faktor 3, in der y-Richtung mit dem Faktor 1 (also keine Streckung) und in der z-Richtung mit dem Faktor ⅓ (Abb. 2). Das Produkt dieser drei Faktoren ist 1, das Volumen bleibt daher invariant. Wir erhalten ein zur Kugel volumengleiches Ellipsoid.

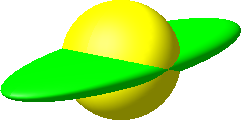
Abb. 2: Volumengleiches Ellipsoid

2 Animation

Die Abbildung 3 zeigt eine Animation dazu.

Abb. 3: Lällekönig

Die gelbe Kugel bleibt dabei invariant, wie ein Blick von der Seite zeigt (Abb. 4).

Abb. 4: Blick von der Seite

In einem Schnitt in der Ebene y = 0 sehen wir einen Kreis und eine Ellipse (Abb. 5). Die Ellipsen sind flächengleich und auch flächengleich zum Kreis.

Abb. 5: Schnitt

3 Schmale Zunge

In den Abbildungen 6 bis 9 wird in der y-Richtung mit dem Faktor 0.7 gestreckt, aber so, dass das Produkt der drei Streckfaktoren konstant gleich eins bleibt. Kugel und Ellipsoid sind immer noch volumengleich.

Abb. 6: Schmale Zunge

Für das grüne Ellipsoid gibt es drei Sonderfälle.

In der Abbildung 7 haben wir ein in der x-Richtung gestrecktes Rotationsellipsoid.

Abb. 7: Gestrecktes Rotationsellipsoid

In der Abbildung 8 haben wir ein in der y-Richtung abgeplattetes Rotationsellipsoid.

Abb. 8: Abgeplattetes Rotationsellipsoid

In der Abbildung 9 haben wir ein in der z-Richtung gestrecktes Rotationsellipsoid.

Abb. 9: Gestrecktes Rotationsellipsoid

4 Breite Zunge

In den Abbildungen 10 bis 13 wird in der y-Richtung mit dem Faktor 1.3 gestreckt, aber so, dass das Produkt der drei Streckfaktoren konstant gleich eins bleibt. Kugel und Ellipsoid sind immer noch volumengleich.

Abb. 10: Breite Zunge

Für das grüne Ellipsoid gibt es wiederum drei Sonderfälle.

In der Abbildung 11 haben wir ein in der z-Richtung abgeplattetes Rotationsellipsoid.

Abb. 11: Abgeplattetes Rotationsellipsoid

In der Abbildung 12 haben wir ein in der y-Richtung gestrecktes Rotationsellipsoid.

Abb. 12: Gestrecktes Rotationsellipsoid

In der Abbildung 13 haben wir ein in der x-Richtung abgeplattetes Rotationsellipsoid.

Abb. 13: Abgeplattetes Rotationsellipsoid

Weblinks

Hans Walser: Flächengleiche Ellipsen

https://walser-h-m.ch/hans/Miniaturen/F/Flaechengleiche_Ellipsen/Flaechengleiche_Ellipsen.html