Hans Walser, [20250403]

Winkelhalbierende

1 Worum es geht

Eine zeichnerische Methode und eine Methode mit Falten und Schneiden, um ein Dreieck zu den drei gegebenen Winkelhalbierenden zu finden. Bei der zweiten Methode benötigen wir nur einen einzigen Schnitt.

Das Dreieck ist durch die drei Winkelhalbierenden nur bis auf Ähnlichkeit festgelegt.

2 Zeichnerische Methode

2.1 Eine Schließungsfigur

Gegeben sind drei kopunktalen Geraden g₀, g₁, g₂. In der Abbildung 1 sind die drei Geraden der Übersichtlichkeit halber nur als vom gemeinsamen Punkt ausgehende Halbgeraden gezeichnet. Die Zwischenwinkel zwischen zwei benachbarten Halbgeraden muss größer als 90° sein.

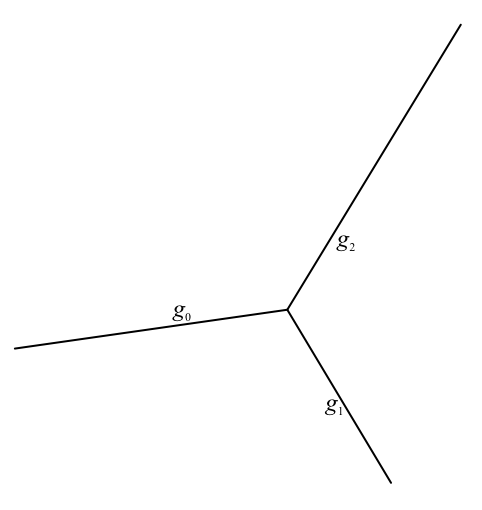
Abb. 1: Drei Geraden

Nun wählen wir einen beliebigen Punkt P₀ (Abb. 2).

Abb. 2: Startpunkt

Diesen Punkt P₀ spiegeln wir an der Geraden g₂ und erhalten den Spiegelpunkt P₁ (Abb. 3).

Abb. 3: Spiegelpunkt

Diesen Punkt P₁ spiegeln wir an der Geraden g₀ und erhalten den Spiegelpunkt P₂ (Abb. 4).

Abb. 4: Nächster Punkt

Das geht nun so weiter. Den Punkt P_k spiegeln wir an der Geraden g_{k–1 (mod 3)} und erhalten den Spiegelpunkt P_k+1 (Abb. 4 bis Abb. 7).

Abb. 5: Nächster Punkt

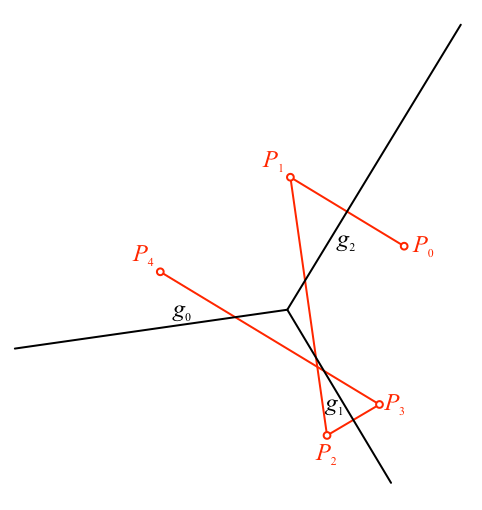
Abb. 6: Nächster Punkt

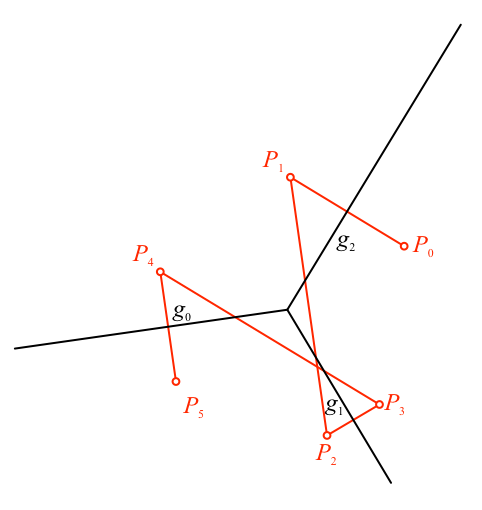
Abb. 7: Nächster Punkt

Und nun erleben wir etwas Interessantes. Wenn wir P₅ an der Geraden g₁ spiegeln, kommen wir zum Punkt P₀ zurück (Abb. 8). Wir haben eine sogenannte Schließungsfigur.

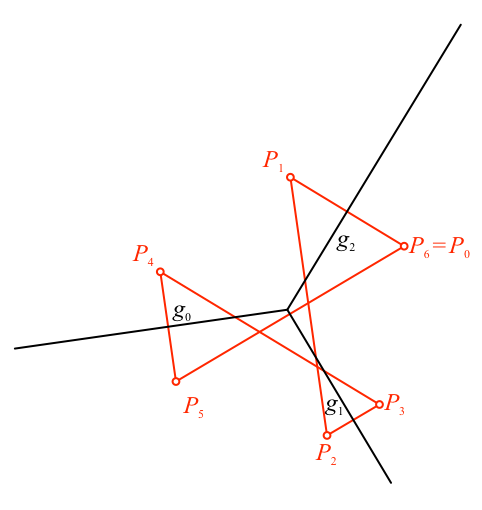
Abb. 8: Schließungsfigur

Beweisskizze: Zusammensetzungen von Geradenspiegelungen sind Drehungen um den Schnittpunkt und den doppelten Winkel von der ersten Spiegelachse zu zweiten. In unserer Situation drehen wir um den gemeinsamen Punkt um insgesamt 720°.

2.2 Das Dreieck

Die Geraden a_i = P_iP_i+3 sind die Seiten des gesuchten Dreieckes (Abb. 9). Der Beweis ergibt sich auf Grund der Spiegelungen.

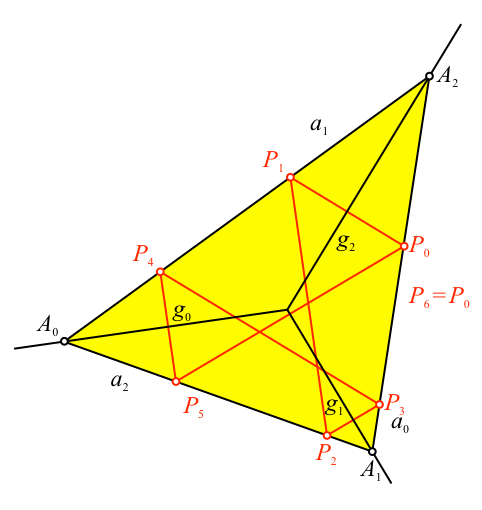
Abb. 9: Das Dreieck

3 Falten und Schneiden

3.1 Falten

Auf einem Blatt Papier bringen wir drei Bergfalten an, die den drei gegebenen Winkelhalbierenden entsprechen (Abb. 10 bis 13). Auch hier gehen wir vom gemeinsamen Punkt aus und falten nach außen, in Richtung der zukünftigen Dreiecksecken. Der Zwischenwinkel zwischen zwei benachbarten Faltlinien muss mehr als 90° betragen.

Abb. 10: Drei Bergfalten

Abb. 11: Drei Bergfalten

In den folgenden Abbildungen sind die Faltlinien zunehmend schärfer gestaltet.

Abb. 12: Drei Bergfalten

Abb. 13: Drei Bergfalten

Wir drehen nun die Figur um und nehmen sie zwischen drei Finger (Abb. 14).

Abb. 14: Zischen drei Fingern

Wir drücken zu Talfalten zusammen (Abb. 15 und 16).

Abb. 15: Zusammendrücken

In der Endlage haben wir drei doppellagige „Flügel“.

Abb. 16: Zu Kanten zusammendrücken

So entstehen drei Talfalten (rot in Abb. 17).

Abb. 17: Drei Talfalten

Link zur zeichnerischen Methode: Diese drei Talfalten sind die Mittelsenkrechten der Strecken P_jP_j+3 , j = 1,2,3 der zeichnerischen Methode (Abb. 18).

Abb. 18: Mittelsenkrechte

In der Situation der Abbildung 16 liegen alle drei roten Faltlinien aufeinander. Wir legen nun die drei Flügel so um, dass sie alle aufeinander liegen und die roten Faltlinien gemeinsam haben (Abb. 19, gemeinsame Faltlinien oben).

Abb. 19: Umlegen der drei Flügel

Wir zeichnen senkrecht zu den oberen gemeinsamen Faltlinien eine Linie (Abb. 20). Theoretisch kann man das auch durch Falten machen, aber die Papierlagen sind mittlerweile so dick, dass dies kaum mehr praktikabel ist.

Abb. 20: Senkrechte Linie

3.2 Ein einziger Schnitt

Nun schneiden wir entlang der senkrechten Linie die Figur entzwei (Abb. 21).

Abb. 21: Entzweischneiden

Aufwickeln des Teils rechts gibt das gesuchte Dreieck (Abb. 22). Das darübergelegte Geodreieck dient nur zum Flachhalten.

Abb. 22: Das Dreieck

Aufwickeln des linken Teils liefert die Negativform (Abb. 23).

Abb. 23: Negativform

Weblinks

Hans Walser: Schließungsfiguren

https://walser-h-m.ch/hans/Schliessungsfiguren/

Hans Walser: Schließungsfiguren der Periodenlänge 6

https://walser-h-m.ch/hans/Schliessungsfiguren/06int_001-050.htm