Hans Walser, [20240610]

Würfelabwicklungen

1 Worum es geht

Die Würfelabwicklungen werden kartografisch belegt.

Geometrische und kombinatorische Fragestellungen.

2 Die sechs Karten

Wir arbeiten mit den sechs Karten der Abbildung 1, welche die gesamte Erdoberfläche abbilden.

Abb. 1: Die sechs Karten

Kartografische Bemerkung: Die sechs Karten sind nach der Collignon-Projektion erstellt. Die Karten sind flächenverhältnistreu (equivalent).

3 Die 20 Abwicklungen

Die Abbildung 2 zeigt die möglichen 20 Würfelabwicklungen, je exemplarisch mit den sechs Karten garniert.

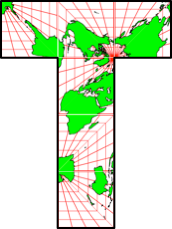
Abb. 2.1: T-Form

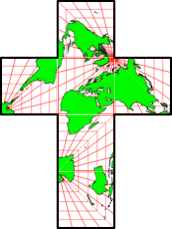
Abb. 2.2: Lateinisches Kreuz

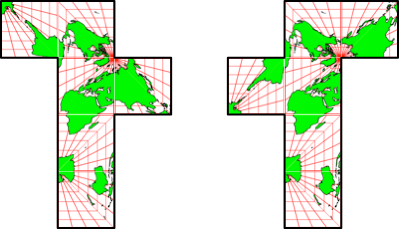
Abb. 2.3

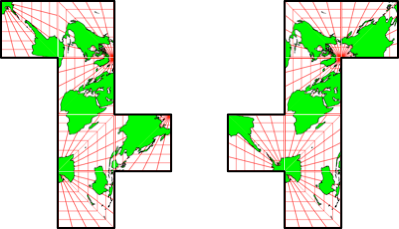
Abb. 2.4

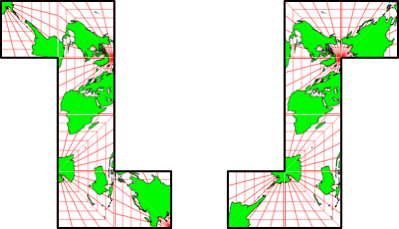
Abb. 2.5: Punktsymmetrische Form

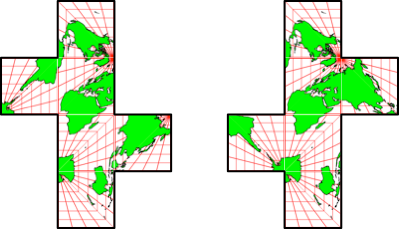
Abb. 2.6: Punktsymmetrische Form

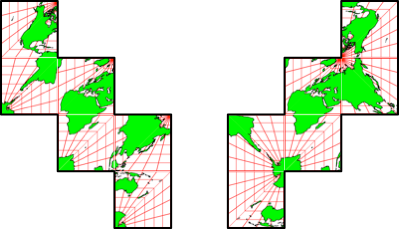
Abb. 2.7: Punktsymmetrische Form

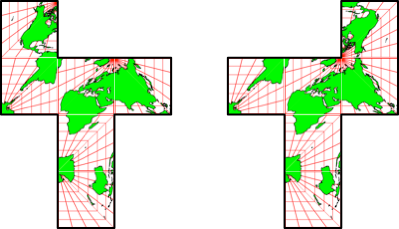
Abb. 2.8

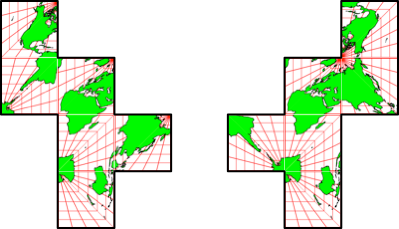
Abb. 2.9

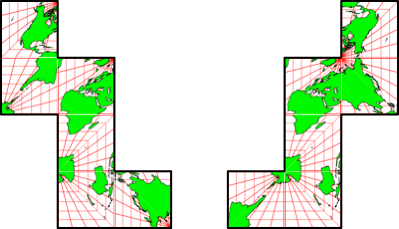
Abb. 2.10

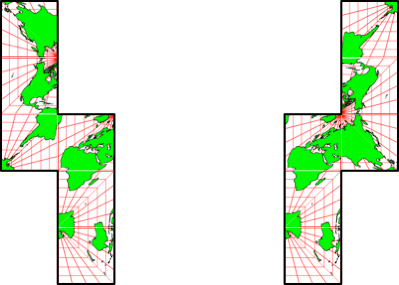
Abb. 2.11: Punktsymmetrische Form

4 Kartenpositionen in einer gegebenen Abwicklungsform

4.1 Problemstellung

Auf wie viele Arten kann der Abwicklungsrahmen (T-Form) der Abbildung 3 mit den sechs Karten konsistent gefüllt werden? „Konsistent“ heißt, dass der Übergang von einer Karte zu einer benachbarten Karte geografisch stimmig ist.

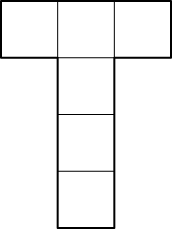
Abb. 3: Gegebener Rahmen der Abwicklung

4.2 Bearbeitung

Mit einer bestimmten der sechs Karten kann das erste Feld links oben auf vier verschiedenen Arten belegt werden (Abb. 4). Die Karte kann um Vielfache von 90° gedreht werden.

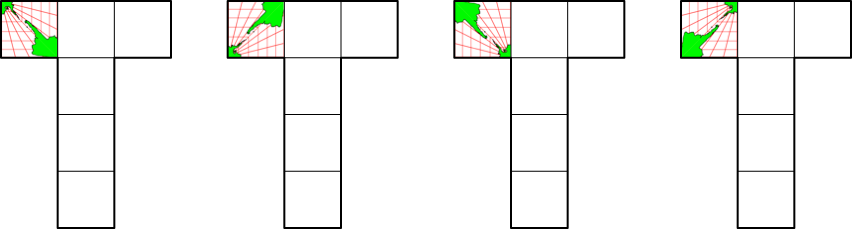
Abb. 4.1: Belegung des ersten Feldes mit einer bestimmten Karte

Durch die Bedingung der Konsistenz ist durch die Belegung des ersten Feldes die gesamte Abwicklung eindeutig festgelegt (Abb. 4.2 bis 4.6).

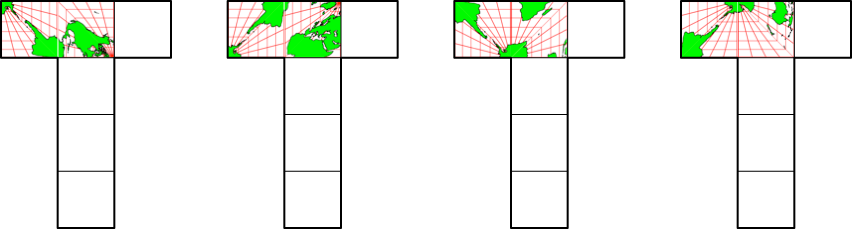
Abb. 4.2: Konsistente Belegung des anschließenden Feldes

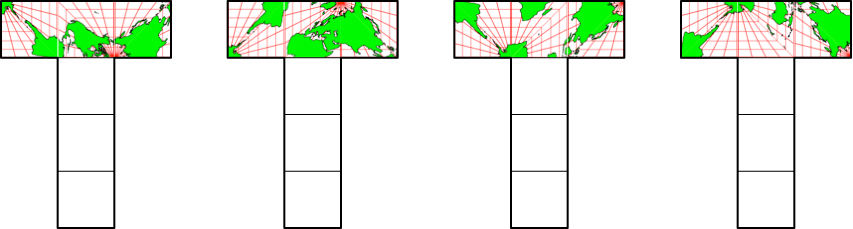
Abb. 4.3: Konsistente Belegung eines dritten Feldes

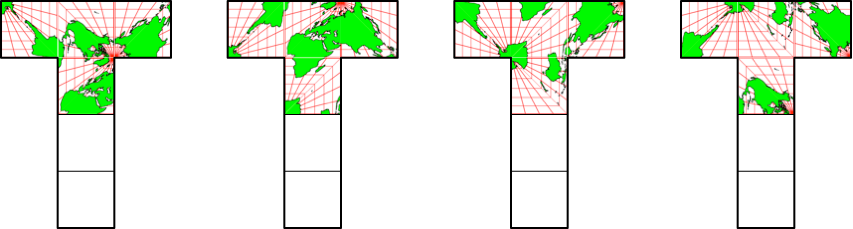
Abb. 4.4: Konsistente Belegung des vierten Feldes

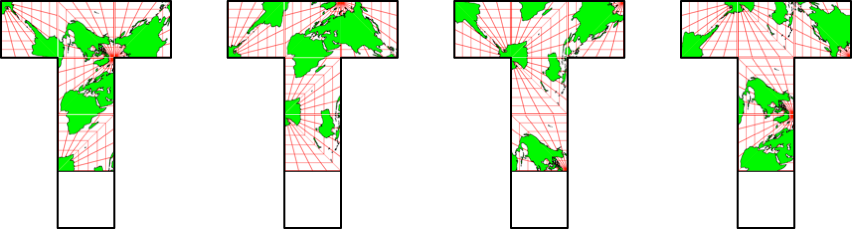
Abb. 4.5: Konsistente Belegung des fünften Feldes

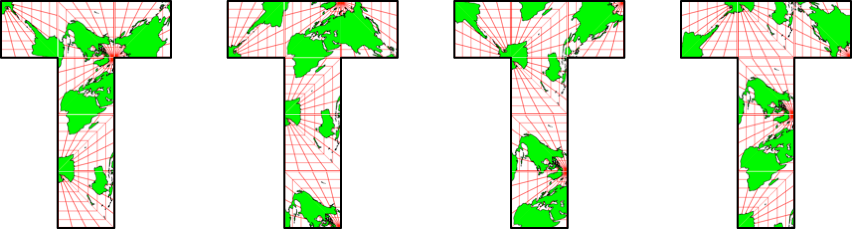
Abb. 4.6: Konsistente Belegung des letzten Feldes

4.3 Punktsymmetrischer Abwicklungsrahmen

Bei einempunktsymmetrischen Abwicklungsrahmen gibt es zu jeder Belegung eine zweite, kongruente Belegung mit einer anderen Startkarte (Abb. 5).

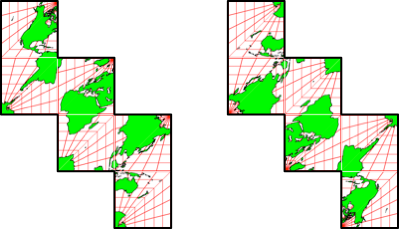
Abb. 5: Punktsymmetrischer Abwicklungsrahmen

5 Kombinatorisches

Da wir für das erste Feld aus sechs Karten wählen können, gibt es bei einem bestimmten, nicht punktsymmetrischen Abwicklungsrahmen insgesamt 4•6 = 24 Möglichkeiten.

Bei einem punktsymmetrischen Abwicklungsrahmen gibt es nur 12 Möglichkeiten.

Gemäß Abbildung 2 gibt es 20 mögliche Abwicklungsrahmen. Allerdings sind 8 davon punktsymmetrisch.

Somit gibt es insgesamt 12•6 + 8•12 = 168 Abwicklungskarten mit den sechs Grundkarten der Abbildung 1.

Weblinks

ETH Zurich. Institute of Cartography and Geoinformation (IKG): Kartenprojektionen

https://www.schweizerweltatlas.ch/swatools/MapProjector/MapProjector.de.html

Hans Walser: Collignon

https://walser-h-m.ch/hans/Miniaturen/C/Collignon/Collignon.html

Hans Walser: Würfelabwicklungen

https://walser-h-m.ch/hans/Miniaturen/W/Wuerfelabwicklungen2/Wuerfelabwicklungen2.html

Hans Walser: Würfelabwicklungen

https://walser-h-m.ch/hans/Miniaturen/W/Wuerfelabwicklungen/Wuerfelabwicklungen.htm