Hans Walser, [20231120], [20240520]
Collignon
1 Worum es geht
Karte von Collignon. Animationen
2 Die Karte von Collignon
Die Abbildung 1 zeigt die Karte von Collignon in eurozentrischer Sicht. In der Kartenmitte erkennen wir den Nullmeridian.
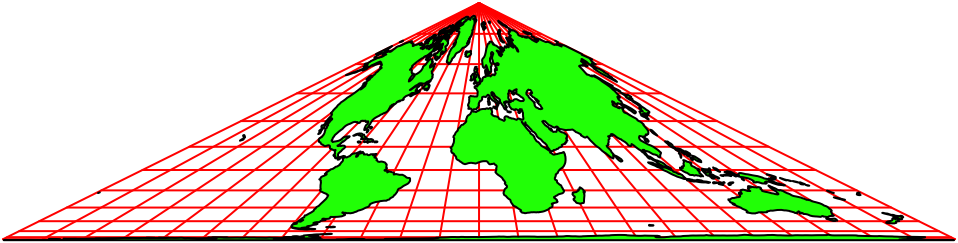
Abb. 1: Karte von Collignon
Die Karte ist flächenverhältnistreu (equivalent).
Die Abbildungsgleichungen sind:
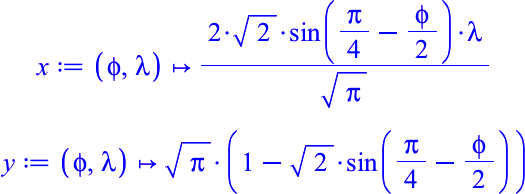
3 Animationen
Die Abbildungen 2 zeigen Animationen in verschiedenen Tempi. Der Nullmeridian (Greenwich) wird schrittweise um 15° verschoben.
Die Animationen erwecken den Anschein einer Drehung auf einem Kegel. Es handelt sich aber um rein zweidimensionale Dreiecks-Karten. Auf jeder Karte ist die ganze Welt abgebildet.
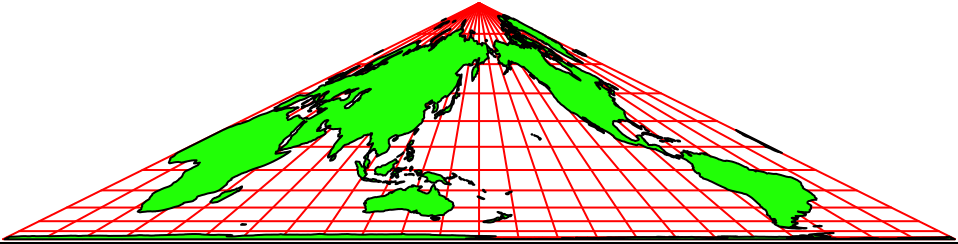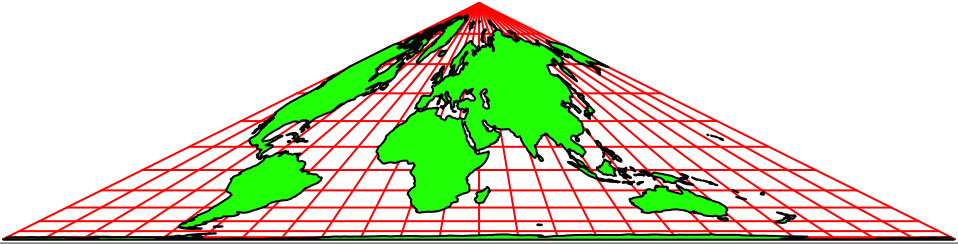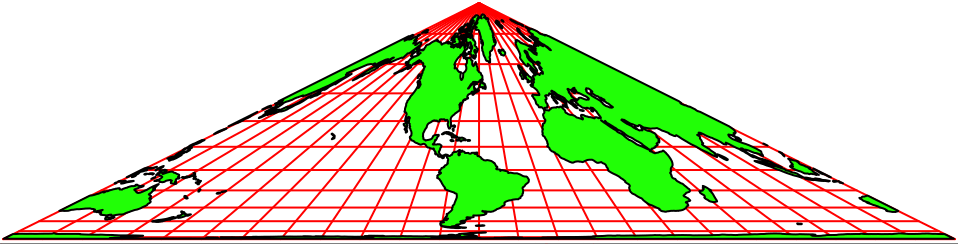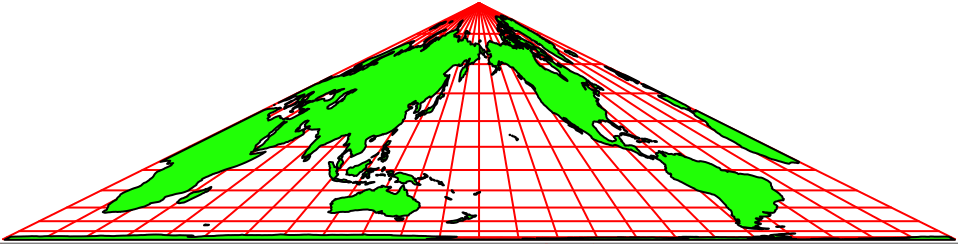
Abb. 2.1: Animation
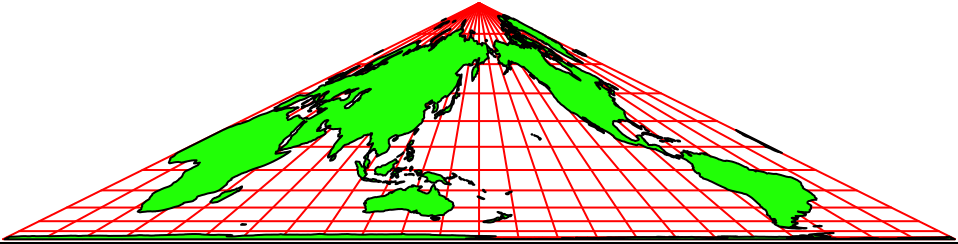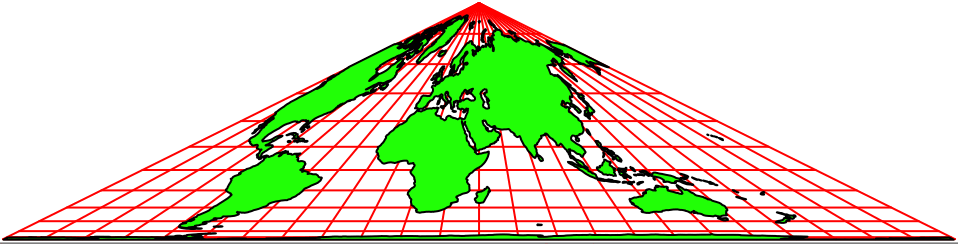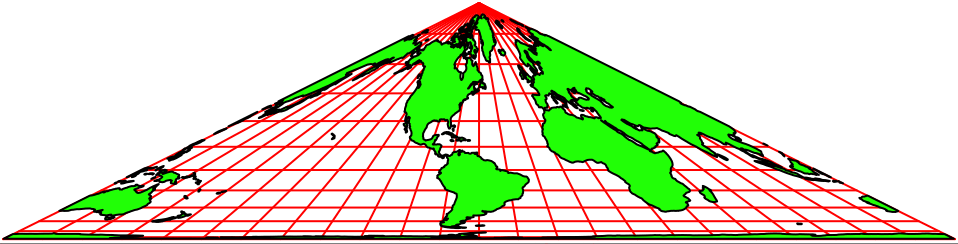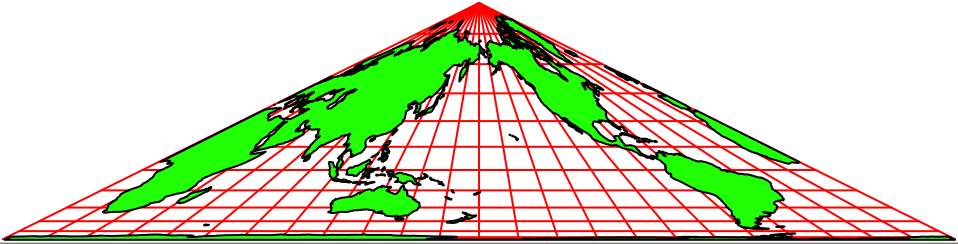
Abb. 2.2: Animation
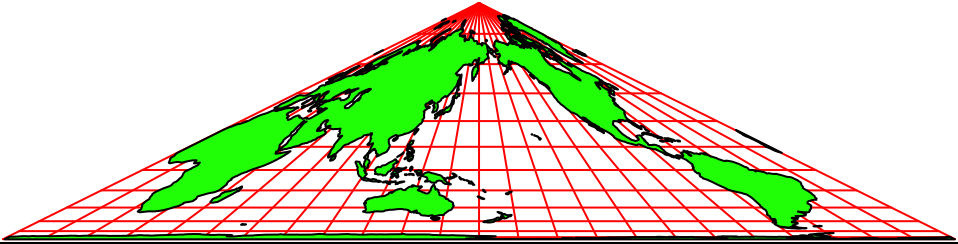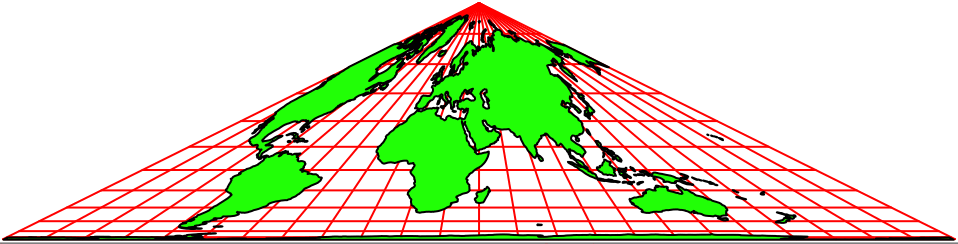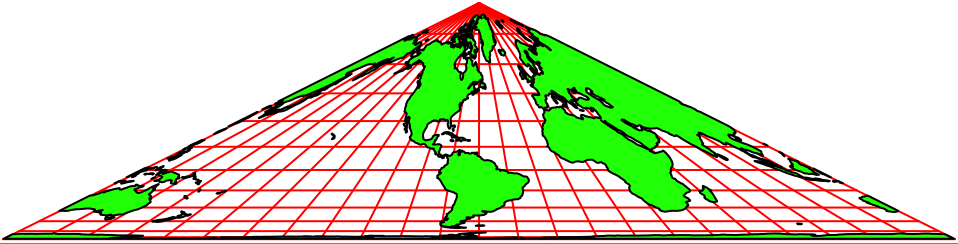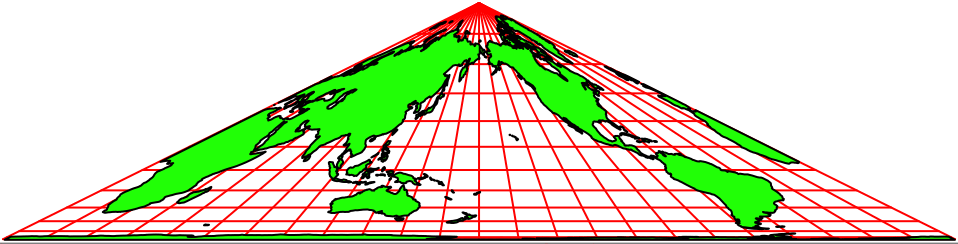
Abb. 2.3: Animation
4 Äquatororientiert
Die Abbildung 3 zeigt eine Anordnung mit der Spitze im Südpol. In der Kartenmitte erkennen wir wieder den Nullmeridian.
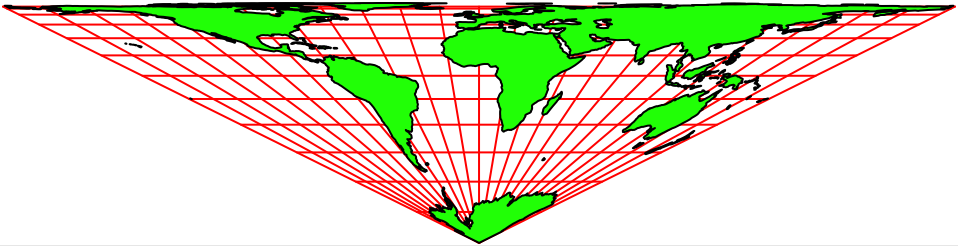
Abb. 3: Spitze im Südpol
Wir schneiden nun in den Karten der Abbildung 1 und der Abbildung 3 je beim Bild des Äquators durch. Dann schieben wir die beiden den jeweiligen Pol enthaltenden Teile zusammen (Abb. 4).
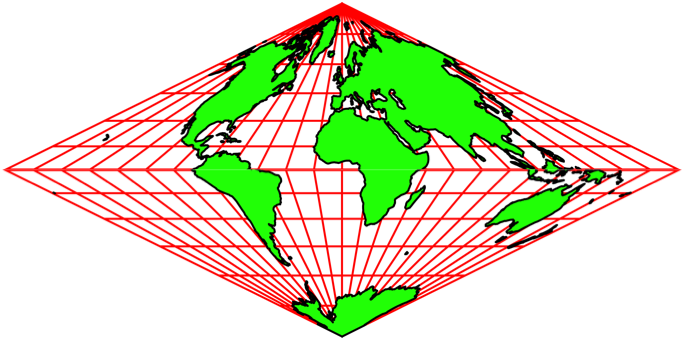
Abb. 4: Pole in den Spitzen
Die Abbildungen 5 zeigen Animationen in
verschiedenen Tempi. Der Nullmeridian (Greenwich) wird schrittweise um 15°
verschoben.
Die Animationen erwecken den Anschein einer
Drehung auf einem Doppelkegel. Es handelt sich aber um rein zweidimensionale Rhomben-Karten.
Auf jeder Karte ist die ganze Welt abgebildet.
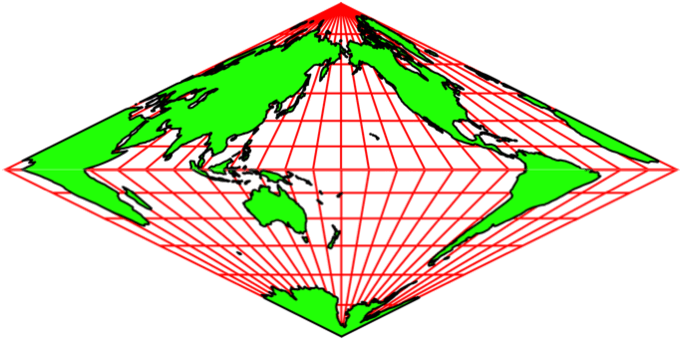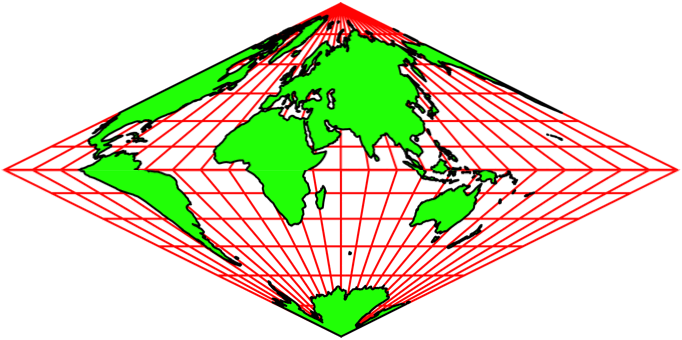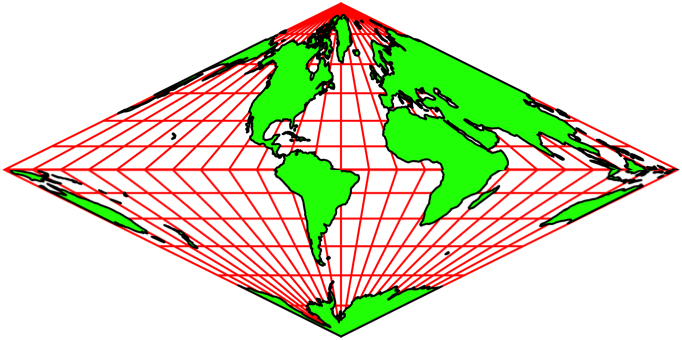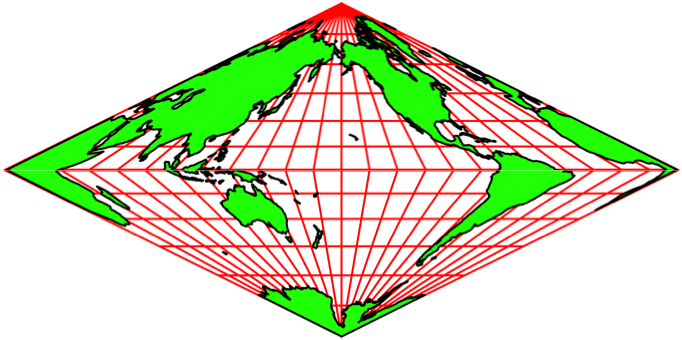
Abb. 5.1: Animation

Abb. 5.2: Schneller
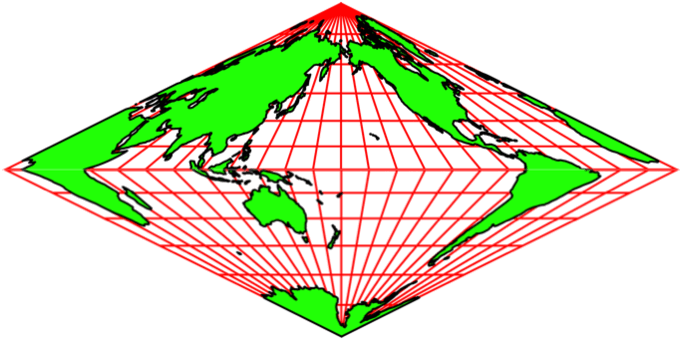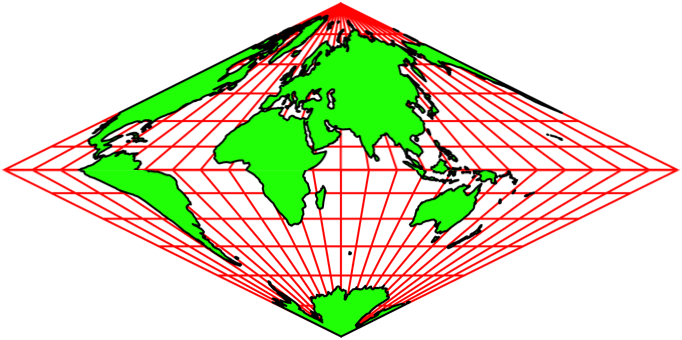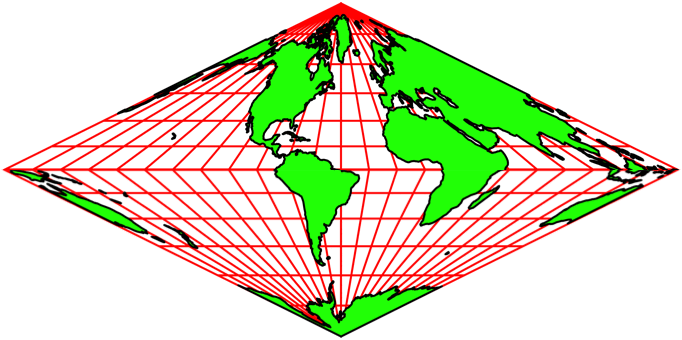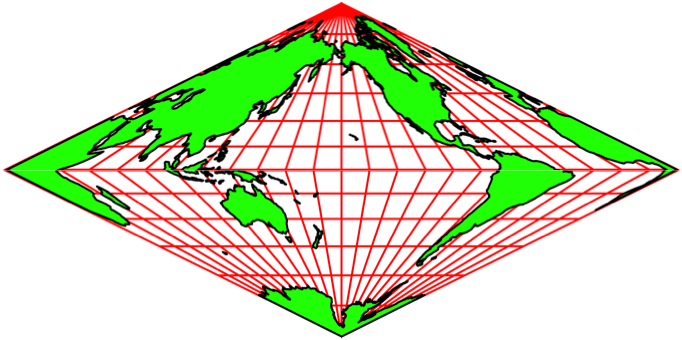
Abb. 5.3: Ganz schnell
5 Person
Édouard Collignon (1831-1913) war ein französischer Ingenieur. Die nach ihm benannte Karte (Collignon-Projektion) veröffentlichte er 1865.
Weblinks
ETH Zurich. Institute of Cartography and
Geoinformation (IKG): Kartenprojektionen
https://www.schweizerweltatlas.ch/swatools/MapProjector/MapProjector.de.html
Hans
Walser: Collignon-Puzzle
https://walser-h-m.ch/hans/Miniaturen/C/Collignon-Puzzle/Collignon-Puzzle.html
Hans Walser: Einstreifen-Oktaeder
https://walser-h-m.ch/hans/Miniaturen/E/Einstreifen-Oktaeder/Einstreifen-Oktaeder.html
Hans Walser: Würfelwelten
https://walser-h-m.ch/hans/Miniaturen/W/Wuerfelwelten/Wuerfelwelten.htm