Hans Walser, [20250504]
Goldener Schnitt
Idee und Anregung: Kurt Hofstetter, Wien
1
Worum es
geht
Konstruktion des
Goldenen Schnittes in einem Dreiecksraster mit Hilfe eines Kreisbogens.
Analoge Konstruktion
im Sechseckraster.
2
Problemstellung
Eine gegebene
Strecke soll im Verhältnis des Goldenen Schnittes geteilt werden.
3
Konstruktion
3.1 Anpassen eines Dreiecksrasters
Wir passen zur
gegebenen Strecke (schwarz in Abb. 1) ein Dreiecksraster an.

Abb. 1:
Anpassen eines Dreiecksrasters
3.2 Kreisbogen
Nun zeichnen wir
einen Kreisbogen mit dem Zentrum im Rasterpunkt rechts unten durch den zweiten
Rasterpunkt links oben (Abb. 2).

Abb. 2:
Kreisbogen
3.3 Goldener Schnitt
Dieser Kreisbogen
teilt die gegebene Strecke im Verhältnis des Goldenen Schnittes (Abb. 3).

Abb. 3: Goldener Schnitt
3.4 Beweis
Im Prinzip eine Variante der Konstruktion des Goldenen Schnittes nach George Odom.
4 Im Sechseckraster
Die Konstruktion funktioniert analog im Sechseckraster (Abb. 4 bis 6).

Abb. 4: Anpassen eines Sechseckrasters
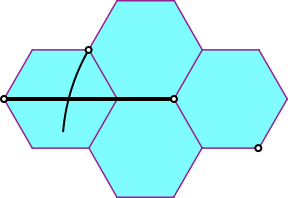
Abb. 5: Kreisbogen
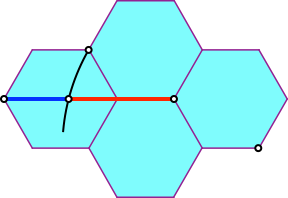
Abb. 6: Goldener Schnitt
Weblinks
Kurt Hofstetter: Divison
of a Segment in the Golden Section with Ruler and Rusty Compass
https://web.archive.org/web/20200716225313/http:/forumgeom.fau.edu/FG2005volume5/FG200518.pdf
Hans Walser: Miniaturen. Goldener Schnitt
https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html
Hans Walser: Goldener Schnitt
https://walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_26/Goldener_Schnitt_26.html
Hans Walser:
Goldener Schnitt
https://walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_27/Goldener_Schnitt_27.html
Literatur
Hans Walser: The
Golden Ratio
https://link.springer.com/book/10.1007/978-3-662-69890-7
Hans Walser: Der
Goldene Schnitt