1 Worum geht es?

Geometrische Visualisierung der üblichen Parametrisierung der pythagoreischen Dreiecke.

Faltvorgehen.

2 Erinnerung

Mit

ist

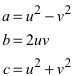
ein primitives pythagoreisches Tripel. Die Zahlen u und v heißen die Parameter des pythagoreischen Tripels und des zugehörigen pythagoreischen Dreieckes.

Die Tabelle 1 zeigt die ersten Werte.

u	v	a	b	c
2	1	3	4	5	Ägyptisches Dreieck. „Lehrerdreieck“
3	2	5	12	13	Indisches Dreieck
4	1	15	8	17
4	3	7	24	25
5	2	21	20	29
5	4	9	40	41

Tab. 1: Pythagoreische Dreiecke

3 Geometrisches Vorgehen

Wir zeichnen ein Rechteck der Länge u und der Breite v und spiegeln es an einer Diagonale. So entstehen außen vier kongruente rechtwinklige Dreiecke mit dem Seitenverhältnis des zu u und v gehörenden pythagoreischen Dreiecks.

Die Abbildung 1 zeigt das Beispiel für u = 2 und v = 1 (ägyptisches Dreieck). Die gelben rechtwinkligen Dreiecke haben das Seitenverhältnis 3 : 4 : 5.

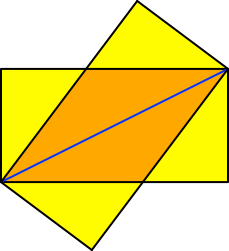
Abb. 1: u = 2, v = 1

Die Abbildung 2 zeigt das Beispiel für u = 3 und v = 2 (indisches Dreieck). Die gelben rechtwinkligen Dreiecke haben das Seitenverhältnis 5 : 12 : 13.

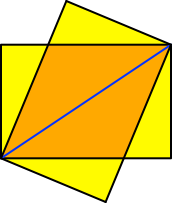
Abb. 1: u = 3, v = 2

4 Beweis

Wir arbeiten mit den Bezeichnungen der Abbildung 3.

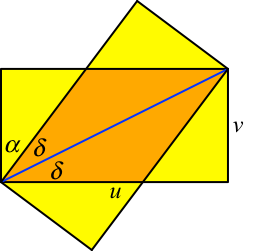
Abb. 3: Bezeichnungen

Zunächst ist:

Weiter erhalten wir:

Damit haben wir das Seitenverhältnis für das zugehörige pythagoreische Dreieck. Dies war zu zeigen.

5 Faltvorgang

Wir arbeiten mit einem Papierrechteck der Länge u und der Breite v, welches auf der Oberseite gelb und auf der Unterseite hellblau ist. Nun falten wir zwei diametrale Ecken aufeinander (Abb. 4). Das sichtbar übrigbleibende gelbe rechtwinklige Dreieck ist das zugehörige pythagoreische Dreieck.