Hans Walser, [20231123]
Rechtwinkliges Dreieck und Goldener Schnitt
Idee und Anregung: Maik Rentsch
1 Worum es geht
Ein Sonderfall einer Schnittpunktkonfiguration im rechtwinkligen Dreieck führt zum Goldenen Schnitt.
2 Der Schnittpunkt
Wir beschreiben einem rechtwinkligen Dreieck ein Quadrat ein, welches auf der Hypotenuse aufsitzt (Abb. 1).
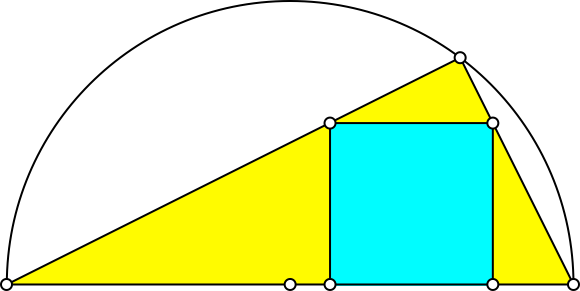
Abb. 1: Quadrat im Dreieck
Wir können nun drei Geraden einzeichnen, welche einen gemeinsamen Schnittpunkt haben (Abb. 2 und 3).
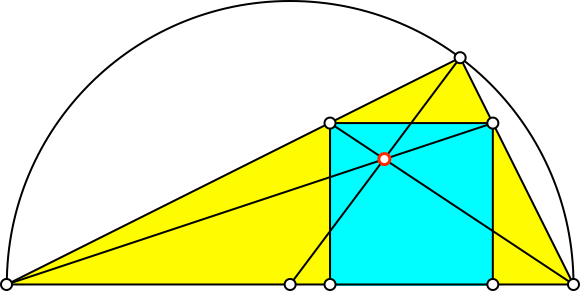
Abb. 2: Schnittpunkt
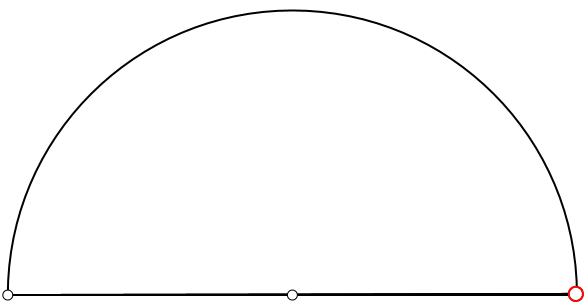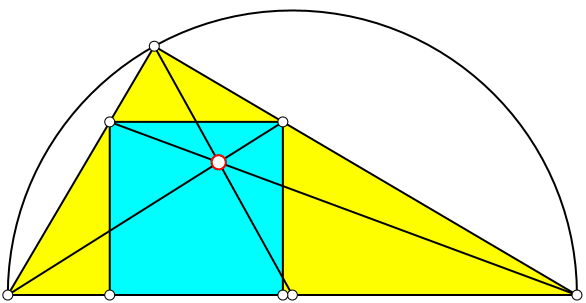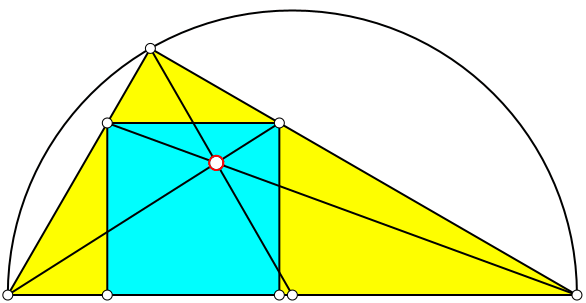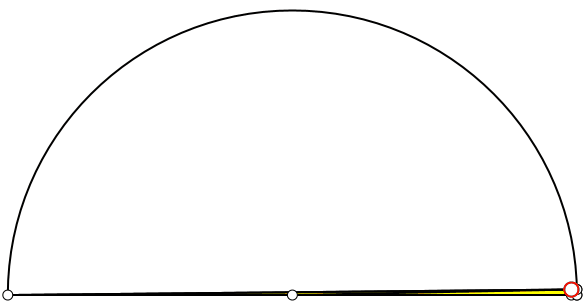
Abb. 3: Schnittpunkt bei Variation des Dreiecks
Der Beweis für die Schnittpunkteigenschaft folgt aus dem Satz von Ceva. Der Teilpunkt auf der Hypotenuse des rechtwinkligen Dreiecks hat als Mittelpunkt das Teilverhältnis 1 : 1. Die beiden Teilpunkte auf den Katheten haben zueinander inverse Teilverhältnisse. Dies folgt aus dem Strahlensatz und der Orientierung der Teilverhältnisse. Insgesamt ist das Produkt der Teilverhältnisse 1. Nach dem Satz von Ceva existiert ein Schnittpunkt.
3 Sonderfall und Goldener Schnitt
Wir betrachten den Sonderfall mit einer unteren Quadratecke im Mittelpunkt der Hypotenuse (Abb. 4).
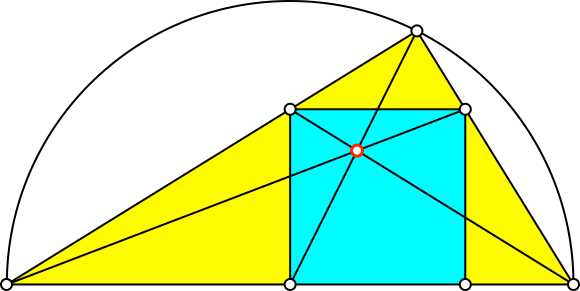
Abb. 4: Sonderfall
In diesem Sonderfall erscheint der Goldene Schnitt an mehreren Orten (Abb. 5.1 bis 5.6). Es sind jeweils der Major rot und der Minor blau eingezeichnet.
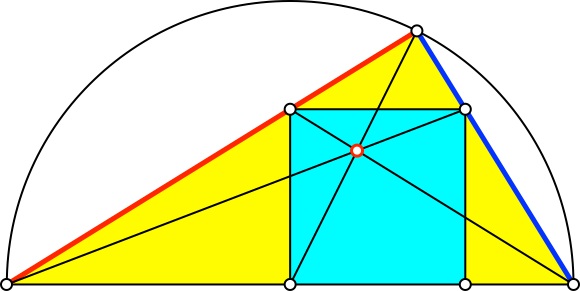
Abb. 5.1: Goldener Schnitt
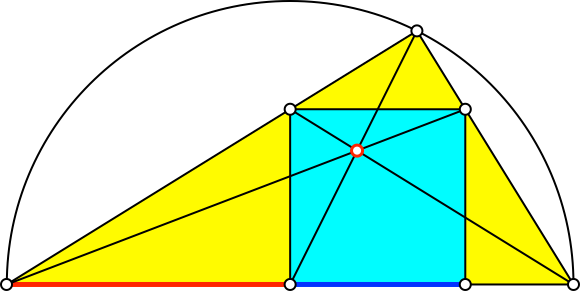
Abb. 5.2: Goldener Schnitt
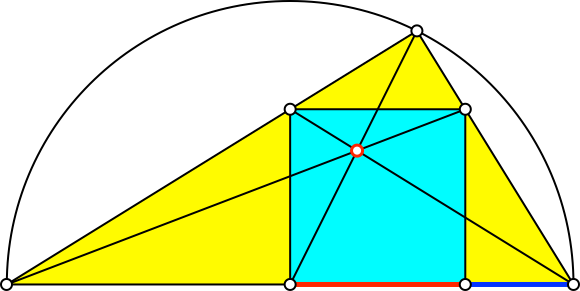
Abb. 5.3: Goldener Schnitt
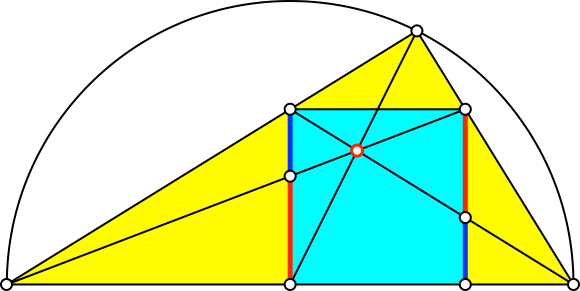
Abb. 5.4: Goldener Schnitt
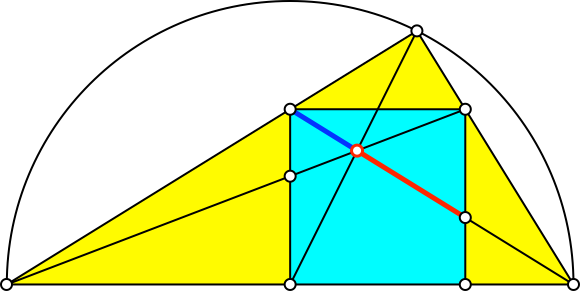
Abb. 5.5: Goldener Schnitt
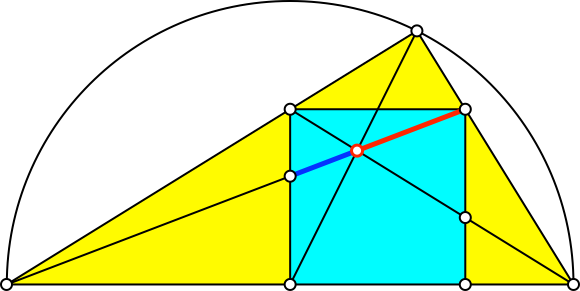
Abb. 5.6: Goldener Schnitt
Weblinks
Hans Walser: Rechtwinkliges Dreieck und Goldener Schnitt
Hans Walser: Rechtwinkliges Dreieck und Goldener Schnitt