Hans Walser, [20250120]
Quadratisches Profil
1 Worum es geht
Wir setzen aus ebenen Polygonen räumliche Figuren zusammen, welche aus drei paarweise orthogonalen Sichtrichtungen gesehen ein quadratisches Profil ausfüllen.
Welches ist die Minimallösung?
Für Flächen- und Volumenberechnungen wird die Quadratseite des Profils auf 1 gesetzt.
2 Beispiele
2.1 Drei Quadrate
Das naheliegende Beispiel besteht aus drei Quadraten mit gemeinsamem Mittelpunkt und paarweise orthogonalen Trägerebenen (Abb. 1 und Abb. 2).

Abb. 1: Drei Quadrate

Abb. 2: Drei Quadrate
Die Abbildung 3 zeigt die drei speziellen Sichten.



Abb. 3: Sicht von vorne, von der Seite und von oben
Die Figur hat den Flächeninhalt 3.
Die Figur hat ein Kuboktaeder als konvexe Hülle (Abb. 4 und Abb. 5).
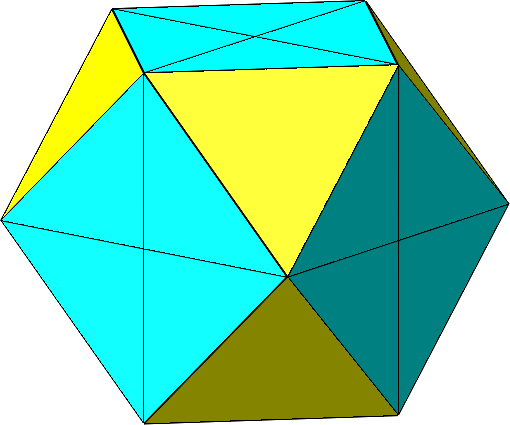
Abb. 4: Kuboktaeder als konvexe Hülle

Abb. 5: Gedrehtes Kuboktaeder
Die drei speziellen Sichten von vorne, von der Seite und von oben sehen alle gleich aus (Abb. 6).
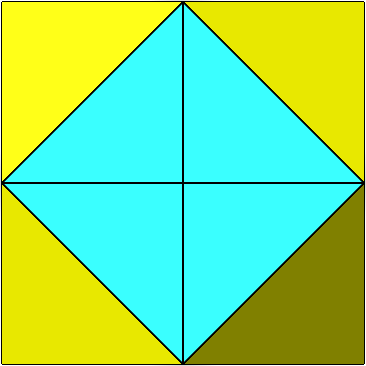
Abb. 6: Quadratisches Profil
Das Kuboktaeder hat das Volumen ⅚.
2.2 Zwei Rechtecke
Die Abbildungen 7 und 8 zeigen eine Figur aus zwei Rechtecken. Die Rechtecke haben das Seitenverhältnis √2:1 (DIN-Format).

Abb. 7: Zwei Rechtecke

Abb. 8: Zwei Rechtecke
Die Abbildung 9 zeigt spezielle Sichten mit quadratischem Profil.



Abb. 9: Sicht von vorne, von der Seite und von oben
Die Figur hat den Flächeninhalt 2√2 ≈ 2.828.
Die Figur hat ein unregelmäßiges Oktaeder als konvexe Hülle (Abb. 10 und Abb. 11). Das unregelmäßige Oktaeder kann auch als Antiprisma gesehen werden.
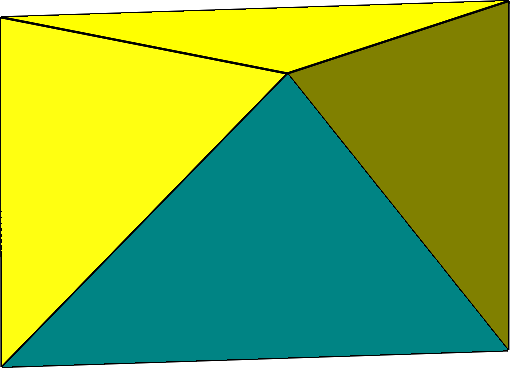
Abb. 10: Unregelmäßiges Oktaeder

Abb. 11: Unregelmäßiges Oktaeder
Die Abbildung 12 zeigt drei spezielle Sichten mit quadratischem Profil.



Abb. 12: Sicht von vorne, von der Seite und von oben
Das unregelmäßige Oktaeder hat das Volumen ⅔.
2.3 Ein Quadrat und ein Rechteck
Ein etwas asymmetrisches Beispiel besteht aus einem Quadrat und einem Rechteck (Abb. 13 und Abb. 14). Das Rechteck hat das Seitenverhältnis √2:1 (DIN-Format):

Abb. 13: Quadrat und Rechteck

Abb. 14: Quadrat und Rechteck
Die Abbildung 15 zeigt drei spezielle Sichten mit quadratischem Profil. Wegen unterschiedlicher Beleuchtung variiert scheinbar die magenta-Farbe.



Abb. 15: Sicht von vorne, von der Seite und von oben
Die Figur hat den Flächeninhalt 1 + √2 ≈ 2.414.
Die konvexe Hülle der Figur ist ein unregelmäßiges Oktaeder (Abb. 16 und Abb. 17).
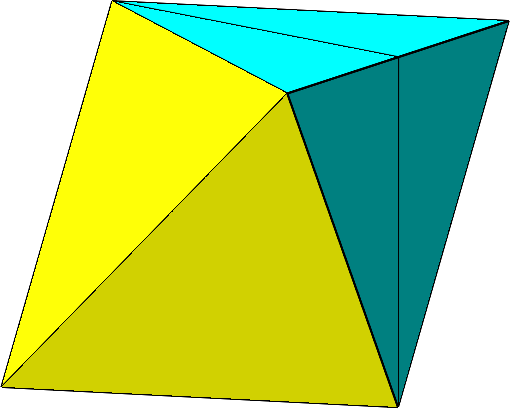
Abb. 16: Unregelmäßiges Oktaeder als konvexe Hülle

Abb. 16: Unregelmäßiges Oktaeder
Die Abbildung 18 zeigt drei spezielle Sichten mit quadratischem Profil.


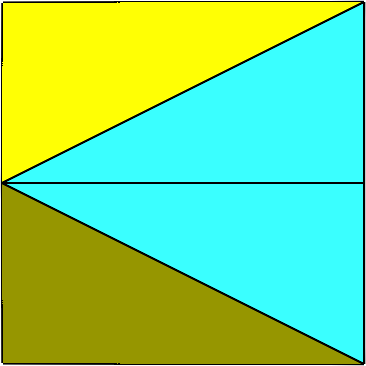
Abb. 18: Sicht von vorne, von der Seite und von oben
Das unregelmäßige Oktaeder hat das Volumen ⅔.
2.4 Sechs gleichschenklige Dreiecke
Die gleichschenkligen Dreiecke (Abb. 19 und 20) haben die Schenkellänge ½√3 ≈ 0.866 und die Basislänge √2 ≈ 1.414.

Abb. 19: Sechs gleichschenklige Dreiecke

Abb. 20: Sechs gleichschenklige Dreiecke
Die Abbildung 21 zeigt verschiedene Sichten mit quadratischem Profil. Wir sehen jeweils vier von den sechs Dreiecken.


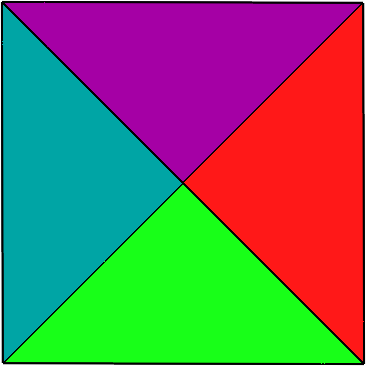
Abb. 21: Sicht von vorne, von der Seite und von oben
Die Figur hat den Flächeninhalt 1.5 √2 ≈ 2.121. Der Autor vermutet, dass dies flächenmäßig die Minimallösung ist.
Die konvexe Hülle der Figur ist das regelmäßige Tetraeder (Abb. 22 und Abb. 23).
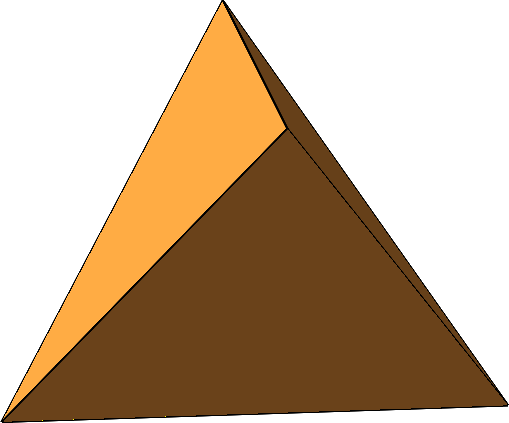
Abb. 22: Regelmäßiges Tetraeder

Abb. 23: Regelmäßiges Tetraeder
Die Abbildung 24 zeigt drei spezielle Sichten mit quadratischem Profil. Bis auf die Schattierung sehen die Bilder gleich aus.



Abb. 24: Sicht von vorne, von der Seite und von oben
Das Tetraeder hat das Volumen ⅓. Der Autor vermutet, dass dies auch volumenmäßig die Minimallösung ist.
Weblinks
Hans Walser: Mehrzweckstöpsel
https://walser-h-m.ch/hans/Miniaturen/M/Mehrzweckstoepsel3/Mehrzweckstoepsel3.html
Hans Walser:
Mehrzweckstöpsel
https://walser-h-m.ch/hans/Miniaturen/M/Mehrzweckstoepsel2/Mehrzweckstoepsel2.html
Hans Walser:
Mehrzweckstöpsel
https://walser-h-m.ch/hans/Miniaturen/M/Mehrzweckstoepsel/Mehrzweckstoepsel.html