Hans
Walser, [20240218]
Varignon
1
Erinnerung:
Der Satz von Varignon
Die Kantenmitten
eines beliebigen Viereckes sind die Ecken eines Parallelogramms (Satz von
Varignon).
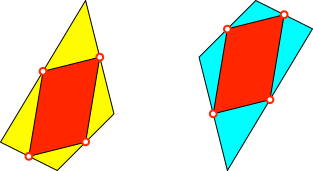
Abb. 1: Satz
von Varignon
Das hellblaue
Viereck ist gegenüber dem gelben um 180° gedreht.
2
Parkett
mit Vierecken
Mit Vierecken können
wir die Ebene parkettieren (Abb. 2). Die hellblauen Vierecke sind gegenüber den
gelben Vierecken um 180° gedreht.
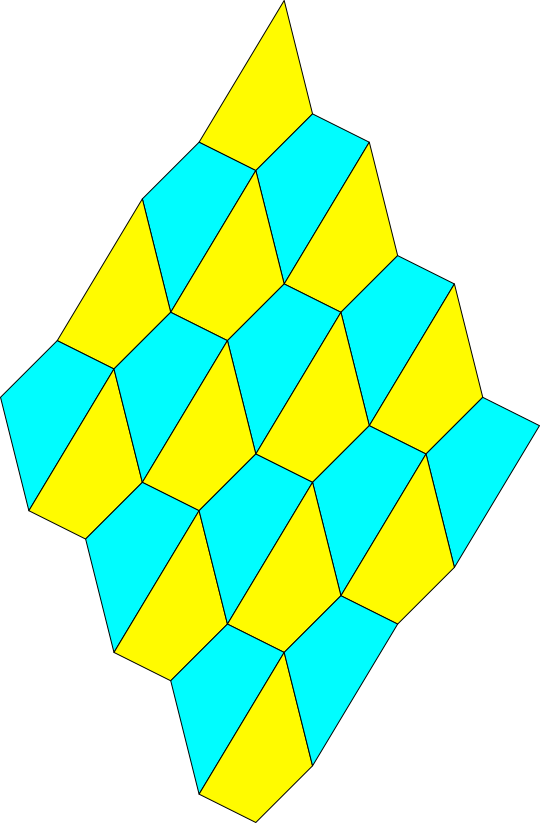
Abb. 2: Parkett
mit Vierecken
Die Varignon-Parallelogramme
bilden ein Parallelogrammraster (Abb. 3). Der Flächeninhalt eines Viereckes ist
doppelt so groß wie der Flächeninhalt des zugehörigen Varignon-Parallelogramms.
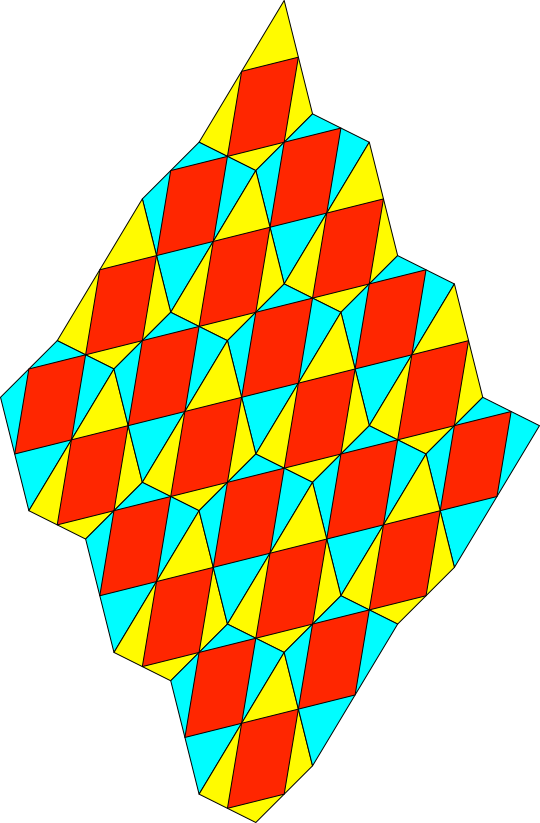
Abb. 3: Parallelogrammraster
3
Mitnahme
eines Punktes
Wir markieren im
Viereck einen beliebigen Punkt (Abb. 4). Der Punkt im hellblauen Viereck ist
relativ an derselben Lage wie der Punkt im gelben Viereck.
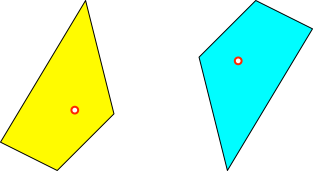
Abb. 4:
Beliebiger Punkt im Viereck
Wir nehmen diesen
Punkt bei der Parkettierung mit (Abb. 5).
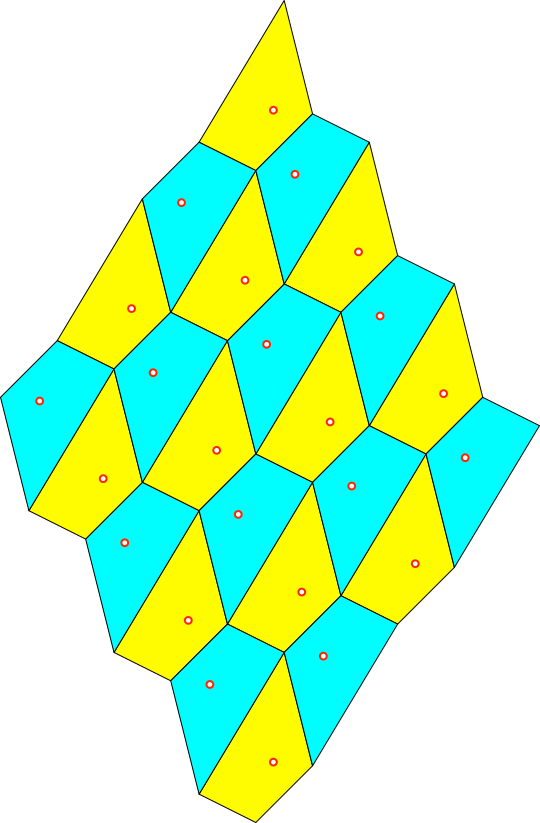
Abb. 5: Punkte
im Parkett
Die Punkte in den
gelben Vierecken bilden ein Parallelogrammraster (Abb. 6), ebenso die Punkte in
den hellblauen Vierecken (Abb. 7). Das Parallelogramm setzt sich aus vier
Varignon-Parallelogrammen der Abbildung 1 zusammen.
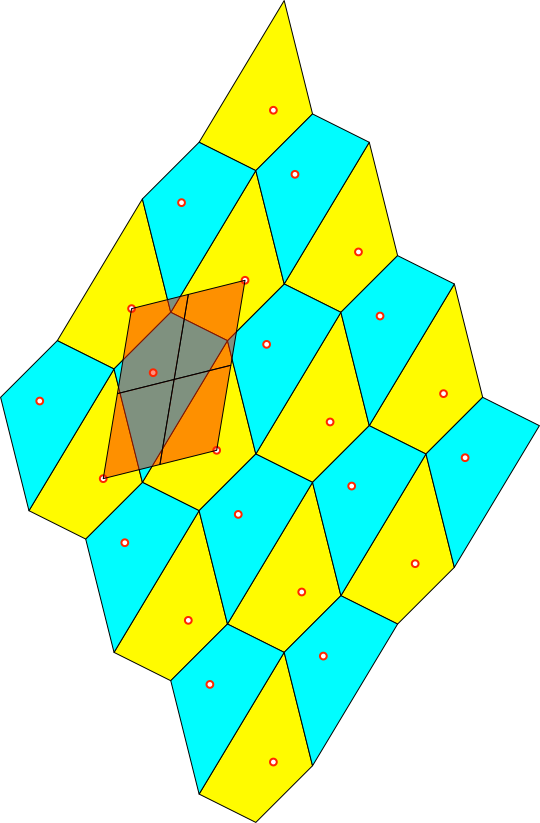
Abb. 6: Parallelogrammraster
in den gelben Vierecken
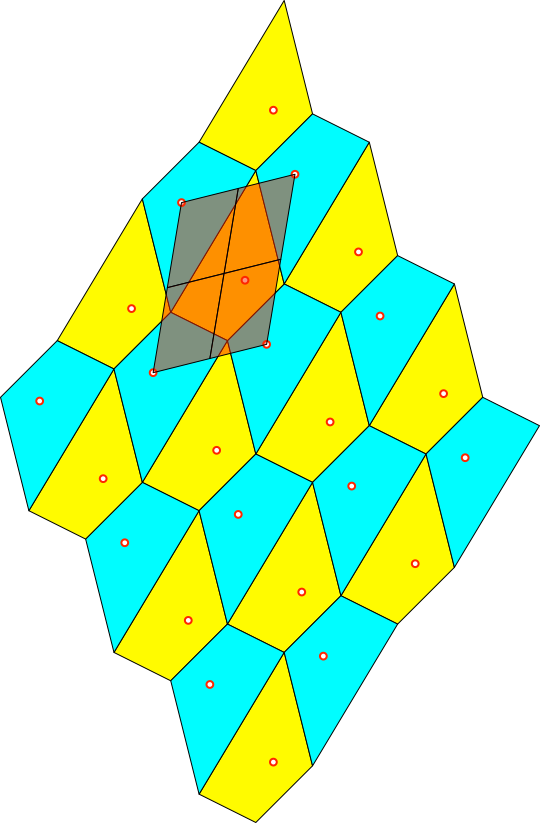
Abb. 7: Parallelogrammraster
in den hellblauen Vierecken
4
Konsistentes
Parallelogrammraster
Die Frage ist nun,
wo der Punkt im Viereck gewählt werden kann, so dass ein konsistentes
Parallelogrammraster entsteht.
Die Lösung ist der
Eckenschwerpunkt des Viereckes (Abb. 8 und 9).
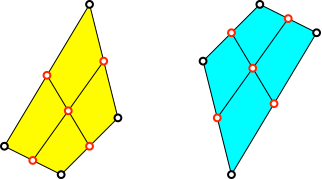
Abb. 4:
Eckenschwerpunkt
Bemerkung: Im
allgemeinen Viereck ist der Eckenschwerpunkt nicht gleich dem
Flächenschwerpunkt.
Das Rasterparallelogramm
hat den gleichen Flächeninhalt wie das Viereck.
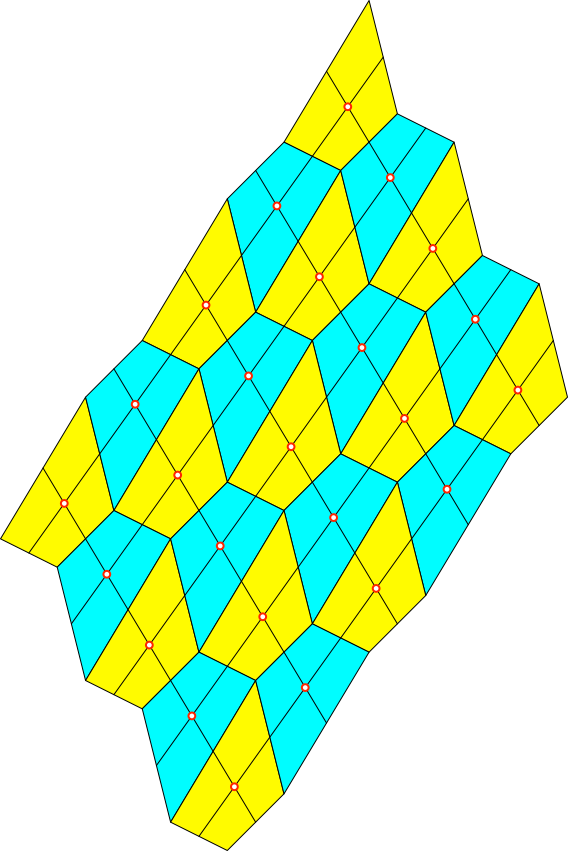
Abb. 9:
Konsistentes Parallelogrammraster
Die Abbildung 10
zeigt den Zusammenhang mit dem Varignon-Parallelogramm.
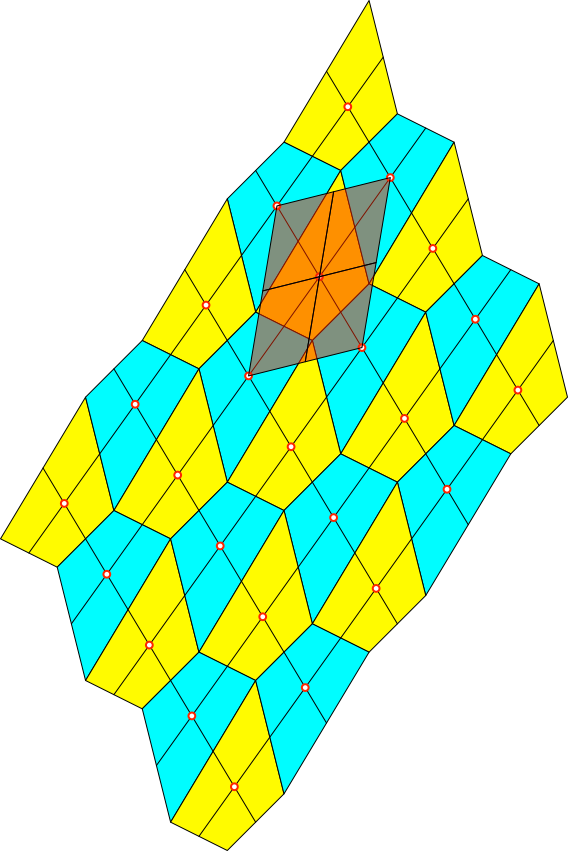
Abb. 10:
Zusammenhang mit Varignon-Parallelogramm
Weblinks
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon/Varignon.htm
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon2/Varignon2.htm
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon3/Varignon3.htm