Hans Walser, [20240521]
Collignon-Puzzle
1 Worum geht es?
Kartografisches Puzzle
2 Die drei Kartenausschnitte
Wir arbeiten mit den drei Kartenausschnitten der Abbildung 1.
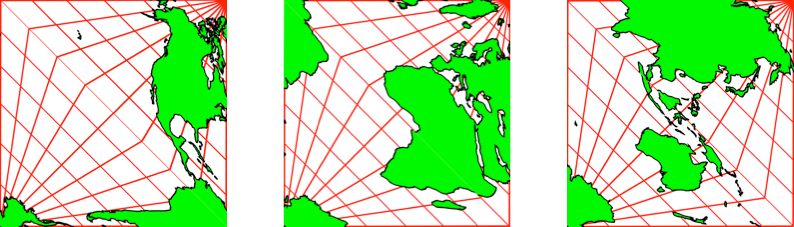
Abb. 1: Die drei Kartenausschnitte
Die drei Kartenausschnitte decken zusammen die ganze Welt ab (Abb. 2).
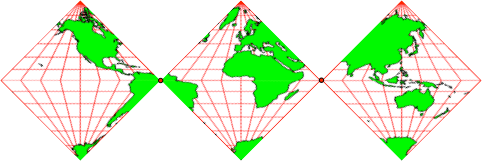
Abb. 2: Ganze Welt
Wir stellen uns die Kontaktpunkte als Gelenke vor. Die Kartenausschnitte können wir auf verschiedene Arten zusammenklappen (Abb. 3). An den gemeinsamen Kanten gehen die Kartenausschnitte jeweils geografisch stimmig (konsistent) ineinander über.
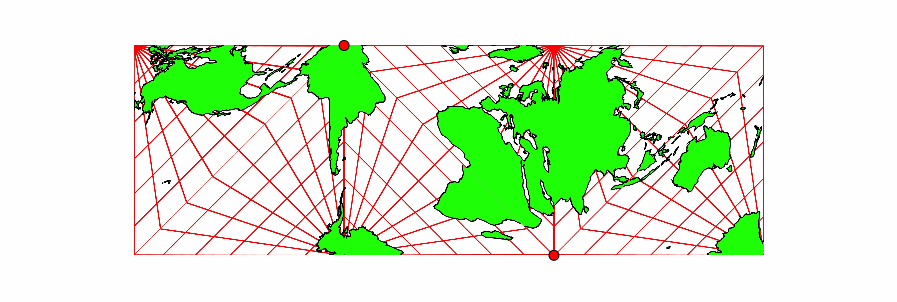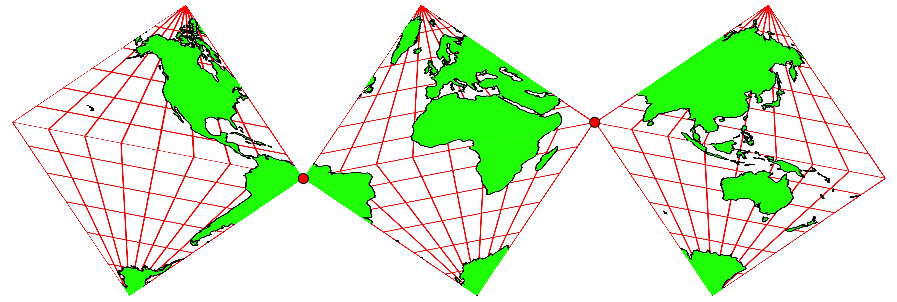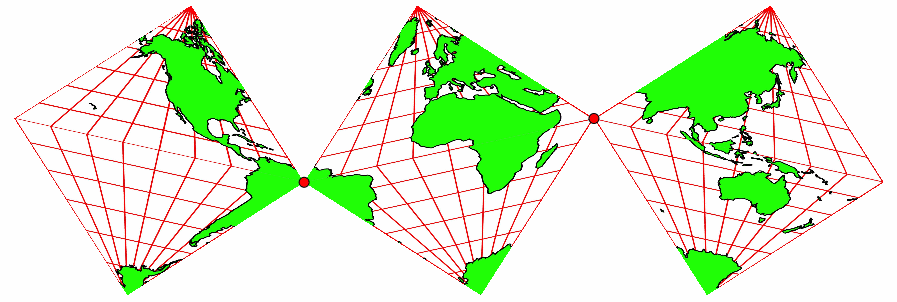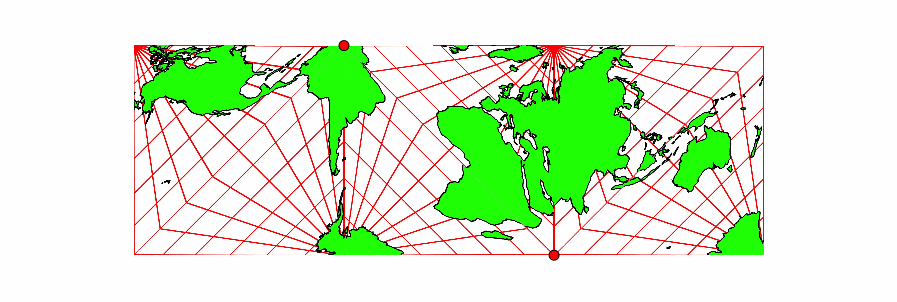
Abb. 3: Gelenkmodell
3 Konsistente Kartenzusammensetzungen
Wir versuchen nun, mehrere Sätze von Kartenausschnitten der Abbildung 1 konsistent zusammenzusetzen.
Wir beginnen mit drei Kartenausschnitten (Abb. 4). Dies ist auch eine der beiden Endlagen des Gelenkmodells (Abb. 3).
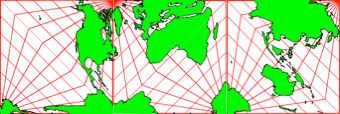
Abb. 4: Drei Kartenausschnitte
Wir können nun einen weiteren Satz aus drei Kartenausschnitten konsistent anfügen (Abb. 5). Die drei neu angefügten Kartenausschnitte liegen in anderer Reihenfolge und Position als die drei ersten.

Abb. 5: Drei weitere Kartenausschnitte
Diese Zusammensetzung von sechs Kartenausschnitten kann nun als Basis für ein Bandornament dienen (Abb. 6).

Abb. 6: Bandornament
Die Abbildung 7.1 zeigt eine Treppe, bestehend aus zwei Sätzen von Kartenausschnitten.
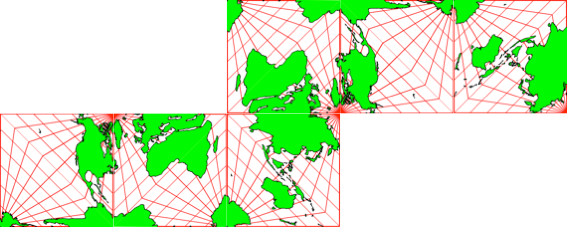
Abb. 7.1: Treppe
Erst nach sechs Stufen (Abb. 7.2) haben wir den Ansatz für eine Bandornament (Abb. 7.3) erreicht.
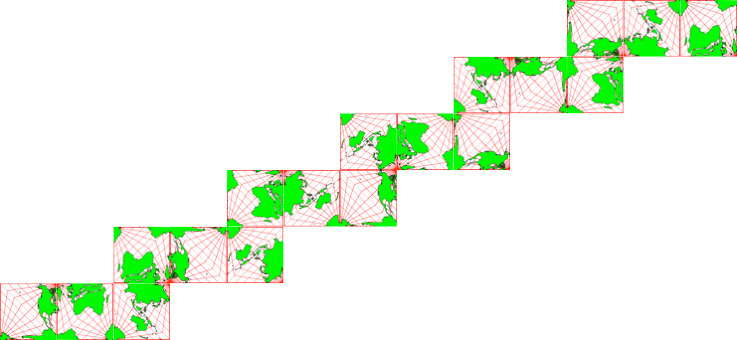
Abb. 7.2: Sechs Stufen

Abb. 7.3: Bandornament
Die Abbildungen 8 und 9 zeigen zwei zirkuläre Anordnungen.
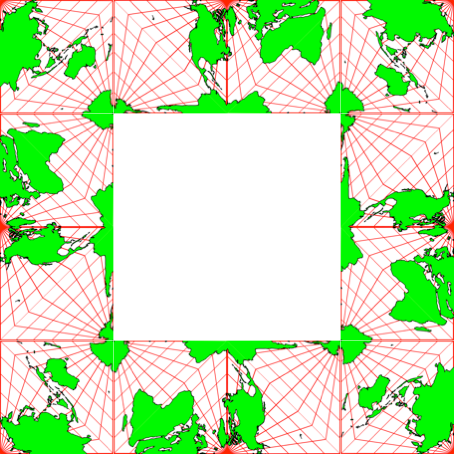
Abb. 8: Quadratische Anordnung
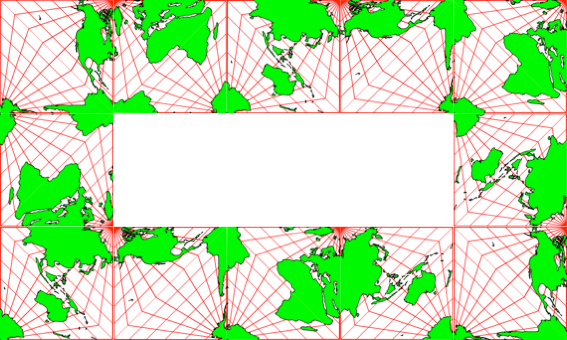
Abb. 9: Rechteckanordnung
4 Konstruktion der Kartenausschnitte
Wir zeigen exemplarisch die Konstruktion der mittleren der drei Kartenausschnitte der Abbildungen 1, 2, 3 und 4. Dieser Ausschnitt hat den Nullmeridian als eine der beiden Diagonalen.
Die Konstruktion basiert auf der Collignon-Projektion.
4.1 Collignon-Projektion
Wir beginnen mit der klassischen Collignon-Projektion (Abb. 10). Diese hat den Nullmeridian als Mittellinie. Die Karte ist in einer 15°-Rasterung gezeichnet.
Die Karte ist flächenverhältnistreu. Dies wird an den eingezeichneten orangen Verzerrungsellipsen sichtbar. Diese haben zwar unterschiedliche Formen, aber alle denselben Flächeninhalt. Der Äquator (blau in Abb. 10) teilt die Dreiecksfläche in zwei flächengleiche Teile. Der Abstand von der Spitze ist √(½) ≈ 70.71% der gesamten Dreieckshöhe.
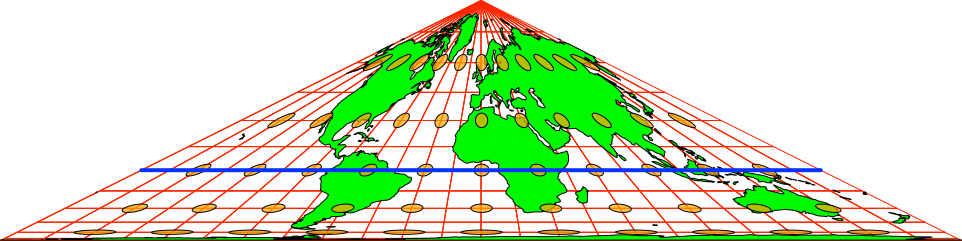
Abb. 10: Collignon-Projektion
Die Abbildung 11 zeigt dieselbe Projektion, aber auf den Südpol fokussiert. Sie hat ebenfalls den Nullmeridian als Mittellinie.
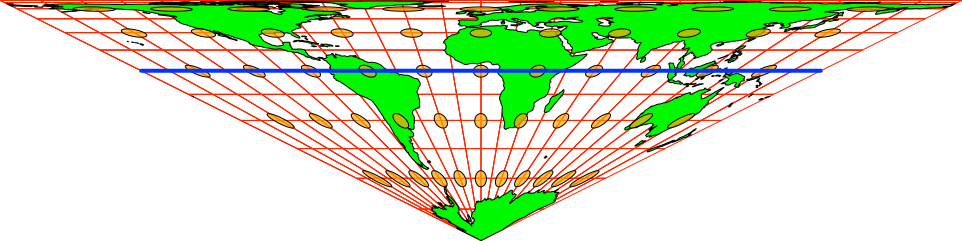
Abb. 11: Fokussierung auf den Südpol
4.2 Zwei Hälften
Nun schneiden wir die beiden Karten am Äquator entzwei und fügen die beiden den jeweiligen Pol enthaltenden Teile zusammen (Abb. 12). Der Nullmeridian ist die senkrechte Mittellinie.
Die Verzerrungsellipsen werden nicht mehr gezeichnet.
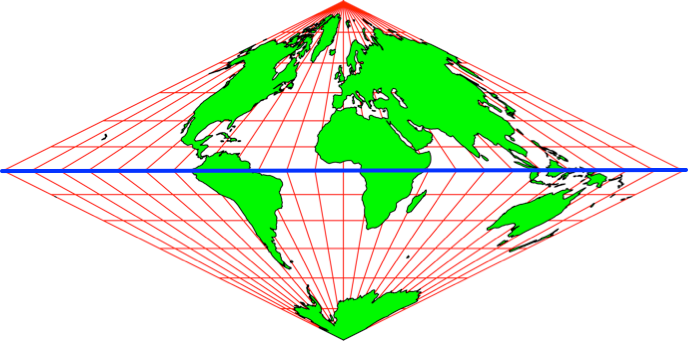
Abb. 12: Zusammensetzung
4.3 Animation
Wir können einen anderen Meridian als Mittellinie wählen. In der Abbildung 13 wird der Mittellinien-Meridian schrittweise um 15° versetzt. Deshalb bleiben die Netzlinien scheinbar stabil. Es entsteht der Eindruck einer Drehung auf einem Doppelkegel.
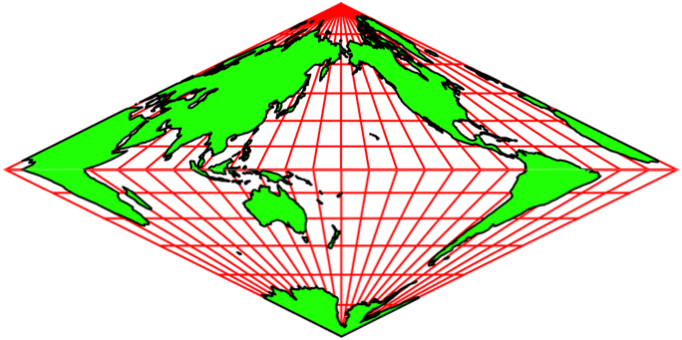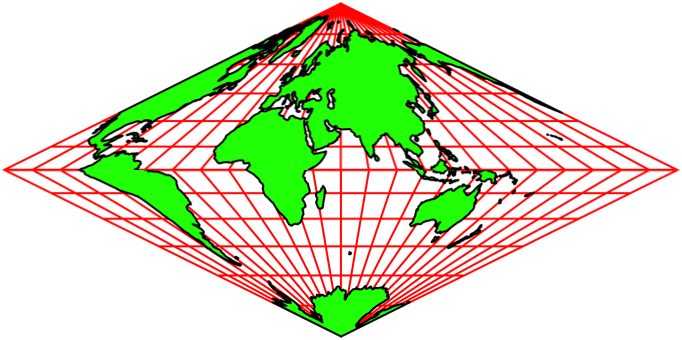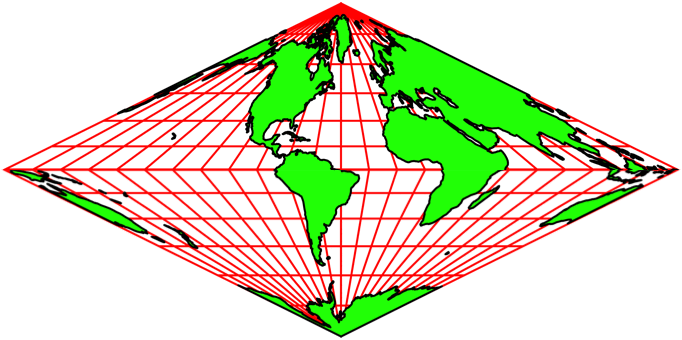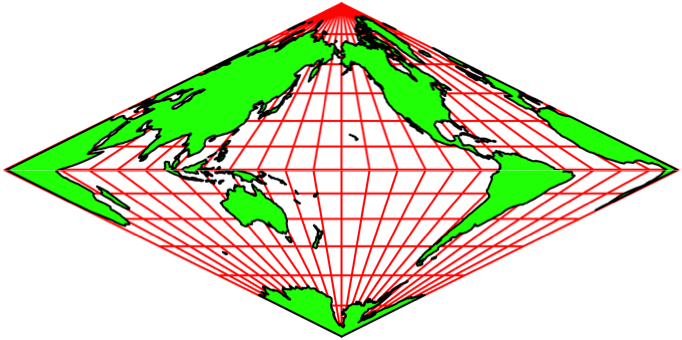
Abb. 13.1: Andere Mittellinien

Abb. 13.2: Schneller
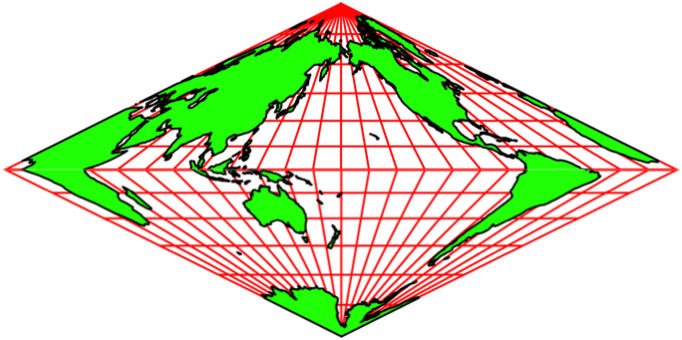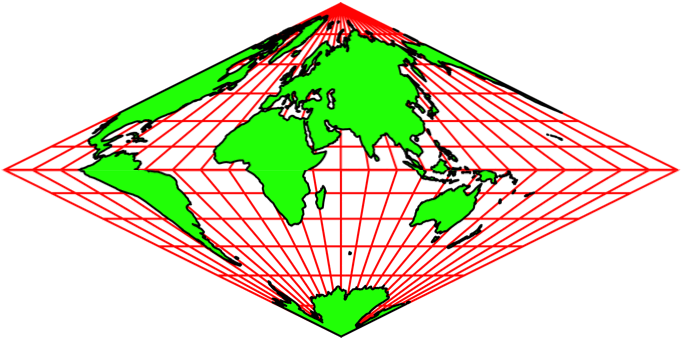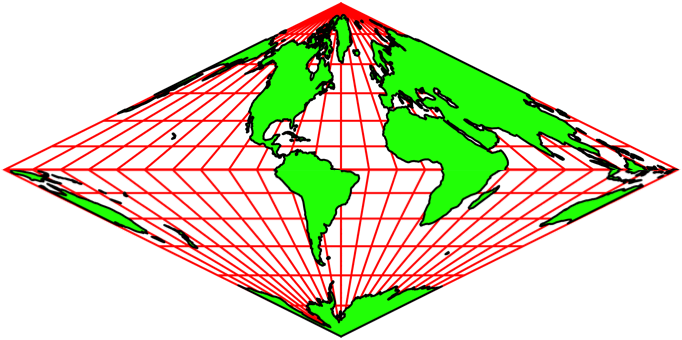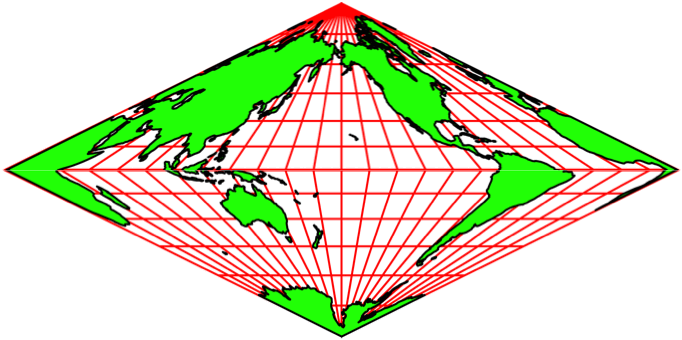
Abb. 13.3: Noch schneller
4.4 Kartenausschnitt
Der von uns gewünschte Kartenausschnitt liegt zwischen den Meridianen 60°W und 60°E (Abb. 14).
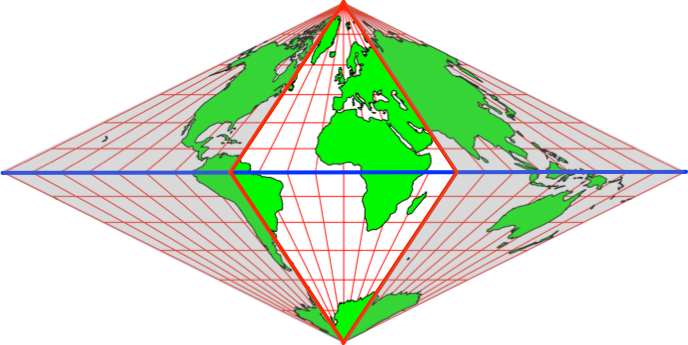
Abb. 14: Kartenausschnitt
Der Kartenausschnitt ist also ein Rhombus. Durch Zusammendrücken in vertikaler Richtung erhalten wir den gesuchten quadratischen Kartenausschnitt (Abb. 15). Die Flächenverhältnisse bleiben dabei unverändert.
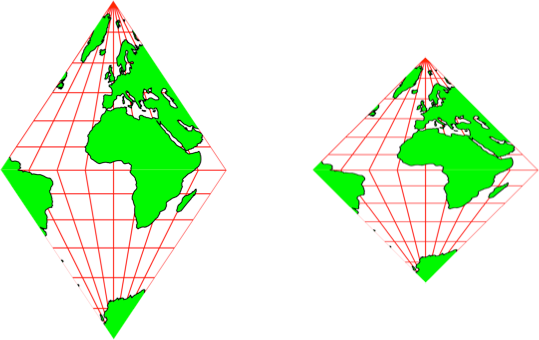
Abb. 15: Vom Rhombus zum Quadrat
5 Schnittmuster
In den Schnittmustern (Abb. 16 und Abb. 17) haben die Quadrate Seitenlängen von 7cm beziehungsweise 8cm.
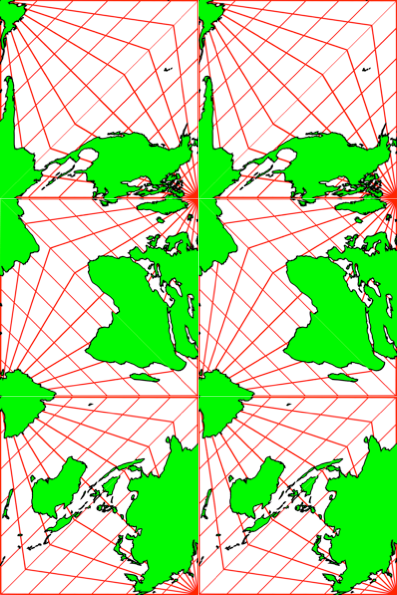
Abb. 16: Kantenlänge 7cm
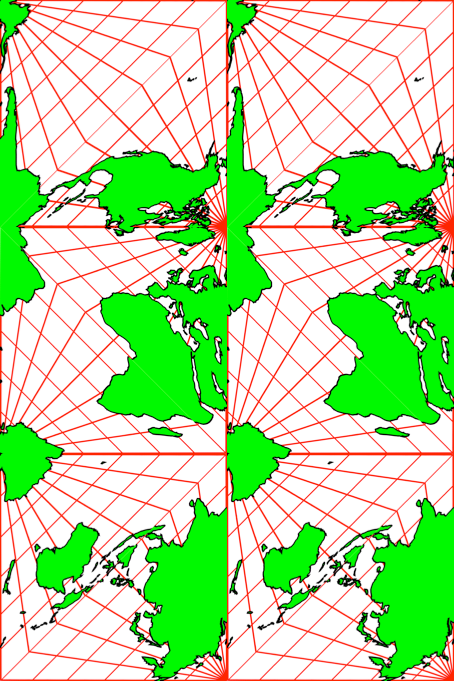
Abb. 17: Kantenlänge 8cm
Weblinks
ETH Zurich.
Institute of Cartography and Geoinformation (IKG): Kartenprojektionen
https://www.schweizerweltatlas.ch/swatools/MapProjector/MapProjector.de.html
Hans
Walser: Collignon
https://walser-h-m.ch/hans/Miniaturen/C/Collignon/Collignon.html
Hans
Walser: Collignon-Puzzle
https://walser-h-m.ch/hans/Miniaturen/C/Collignon-Puzzle/Collignon-Puzzle.html
Hans Walser: Einstreifen-Flechtmodell
https://walser-h-m.ch/hans/Miniaturen/E/Einstreifen/Einstreifen.htm
Hans Walser: Einstreifen-Welt
https://walser-h-m.ch/hans/Miniaturen/E/Einstreifen-Welt/Einstreifen-Welt.html
Hans Walser: Einstreifen-Oktaeder
https://walser-h-m.ch/hans/Miniaturen/E/Einstreifen-Oktaeder/Einstreifen-Oktaeder.html
Hans Walser: Würfelwelten
http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelwelten/Wuerfelwelten.htm