Hans Walser, [20241103]
Füllkreis
1 Worum es geht
Inkreise. Pythagoreische Dreiecke
2 Einstiegsbeispiel
In einem Quadrat zeichnen wir zwei Viertelkreise und die beiden Füllkreise mit Mittelpunkten auf der Symmetrieachse (Abb. 1).

Abb. 1: Viertelkreise und Füllkreise
Das rote Dreieck mit einer Ecke im Mittelpunkt des roten Füllkreises hat das Seitenverhältnis 3:4:5, ist also ein pythagoreisches Dreieck (Abb. 2).

Abb. 2: Pythagoreisches Dreieck
Das blaue Dreieck mit einer Ecke im Mittelpunkt des blauen Füllkreises hat das Seitenverhältnis 15:8:17, ist also ebenfalls ein pythagoreisches Dreieck (Abb. 3).

Abb. 3: Pythagoreisches Dreieck
3 Umgekehrter Einstieg
Wir beginnen mit einem pythagoreischen Dreieck, zum Beispiel dem Dreieck mit dem Seitenverhältnis 5:12:13 (Abb. 4), zeichnen den roten Kreis, passen die Viertelkreise ein und packen das Ganze in ein Rechteck.
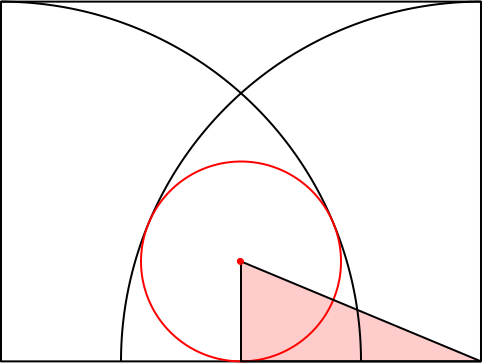
Abb. 4: Umgekehrter Einstieg
Der blaue Füllkreis führt ebenfalls zu einem pythagoreischen Dreieck. Es hat das Seitenverhältnis 3:4:5 (Abb. 5).
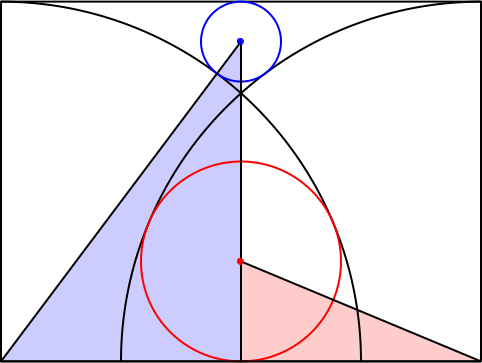
Abb. 5: Seitenverhältnisse 5:12:13 und 15:8:17
Die Abbildung 6 zeigt ein weiteres Beispiel.

Abb. 6: Seitenverhältnisse 15:8:17 und 63:16:65
Und noch ein Beispiel (Abb. 7).

Abb. 7: Seitenverhältnisse 7:24:25 und 55:48:73
4 Tabellarische Darstellung
Wir parametrisieren die roten pythagoreischen Dreiecke in der üblichen Weise (Tab. 1). Anschließend werden vom zugehörigen blauen pythagoreischen Dreieck die Parameter und die Seiten angegeben. Man kann versuchen, ein Muster zu erkennen.
|
u |
v |
a |
b |
c |
u |
v |
a |
b |
c |
|
|
2 |
1 |
3 |
4 |
5 |
4 |
1 |
15 |
8 |
17 |
Abbildung 3 |
|
3 |
2 |
5 |
12 |
13 |
2 |
1 |
3 |
4 |
5 |
Abbildung 5 |
|
4 |
1 |
15 |
8 |
17 |
8 |
1 |
63 |
16 |
65 |
Abbildung 6 |
|
4 |
3 |
7 |
24 |
25 |
8 |
3 |
55 |
48 |
73 |
Abbildung 7 |
|
5 |
2 |
21 |
20 |
29 |
3 |
2 |
5 |
12 |
13 |
|
|
5 |
4 |
9 |
40 |
41 |
5 |
2 |
21 |
20 |
29 |
|
|
6 |
1 |
35 |
12 |
37 |
12 |
1 |
143 |
24 |
145 |
|
|
6 |
5 |
11 |
60 |
61 |
12 |
5 |
119 |
120 |
169 |
|
|
7 |
2 |
45 |
28 |
53 |
4 |
3 |
7 |
24 |
25 |
|
|
7 |
4 |
33 |
56 |
65 |
7 |
2 |
45 |
28 |
53 |
|
|
7 |
6 |
13 |
84 |
85 |
5 |
2 |
21 |
20 |
29 |
|
|
8 |
1 |
63 |
16 |
65 |
16 |
1 |
255 |
32 |
257 |
|
|
8 |
3 |
55 |
48 |
73 |
16 |
3 |
247 |
96 |
265 |
|
|
8 |
5 |
39 |
80 |
89 |
16 |
5 |
231 |
160 |
281 |
|
|
8 |
7 |
15 |
112 |
113 |
16 |
7 |
207 |
224 |
305 |
|
|
9 |
2 |
77 |
36 |
85 |
5 |
4 |
9 |
40 |
41 |
|
|
9 |
4 |
65 |
72 |
97 |
9 |
2 |
77 |
36 |
85 |
|
|
9 |
8 |
17 |
144 |
145 |
9 |
4 |
65 |
72 |
97 |
|
|
10 |
1 |
99 |
20 |
101 |
20 |
1 |
399 |
40 |
401 |
|
|
10 |
3 |
91 |
60 |
109 |
20 |
3 |
391 |
120 |
409 |
|
|
10 |
7 |
51 |
140 |
149 |
20 |
7 |
351 |
280 |
449 |
|
|
10 |
9 |
19 |
180 |
181 |
20 |
9 |
319 |
360 |
481 |
|
Tab. 1: Numerische Beispiele
Weblinks
Hans Walser: Füllkreis
https://walser-h-m.ch/hans/Miniaturen/F/Fuellkreis2/Fuellkreis2.html
Hans Walser: Inkreise
https://walser-h-m.ch/hans/Miniaturen/I/Inkreise2/Inkreise2.html
Hans Walser: Berührkreise
https://walser-h-m.ch/hans/Miniaturen/B/Beruehrkreise/Beruehrkreise.html
Hans Walser: Füllkreis
https://walser-h-m.ch/hans/Miniaturen/F/Fuellkreis/Fuellkreis.html