1 Problemstellung

Einer Ellipse ist ein Tangentenviereck einzubeschreiben.

2 Bearbeitung

Es gibt unendlich viele Lösungen.

2.1 Einfaches Vorgehen

Auf der Ellipse wählen wir zwei beliebige Punkte A und C (Abb. 1). Wir haben also zwei Freiheitsgrade.

Ein Bild, das Dunkelheit, Screenshot, Schwarz, Raum enthält.

Automatisch generierte Beschreibung

Abb. 1: Zwei Punkte auf Ellipse

Die Mittelsenkrechte der Strecke AC schneiden wir mit der Ellipse. Schnittpunkte B und D (Abb. 2).

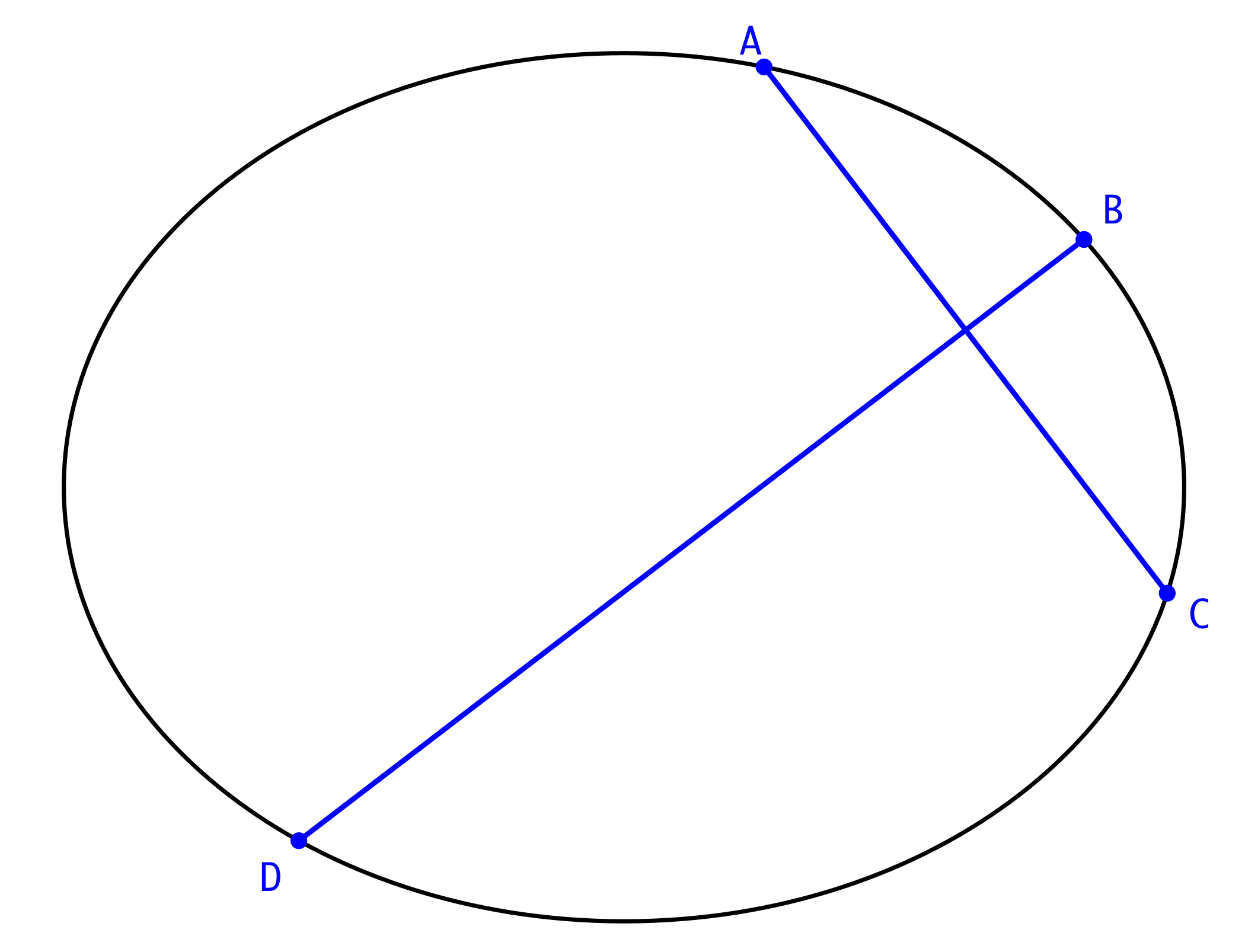
Ein Bild, das Reihe, Screenshot, Licht enthält.

Automatisch generierte Beschreibung

Abb. 2: Mittelsenkrechte

Das Viereck ABCD ist ein Drachenviereck und hat deshalb einen Inkreis (Abb. 3).

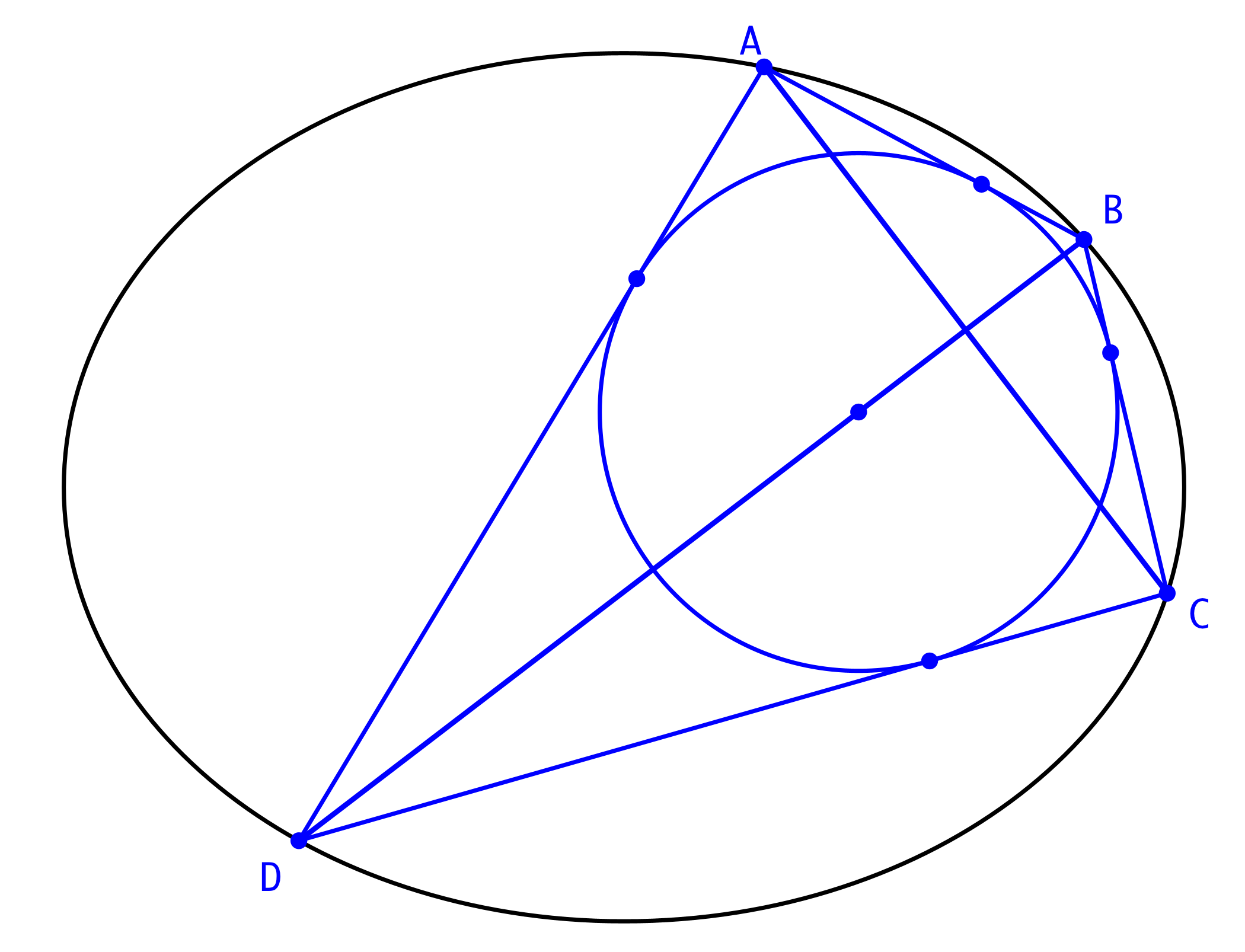
Ein Bild, das Reihe, Dreieck, Astronomie enthält.

Automatisch generierte Beschreibung

Abb. 3: Drachenviereck mit Inkreis

Damit haben wir ein einbeschriebenes Tangentenviereck. Da die Punkte A und C auf der Ellipse frei wählbar sind, gibt es schon mal unendlich viele Lösungen.

Nach einem Satz von Poncelet gibt es zu jeder dieser Lösungen unendlich viele weitere Lösungen mit demselben Inkreis (rot in Abb. 4). Diese Lösungen sind keine Drachenvierecke mehr.

Abb. 4: Weitere Lösungen

2.2 Elaboriertes Vorgehen

Wir wählen auf der Ellipse drei beliebige Punkte A, B und C (Abb. 5). Damit haben wir sogar drei Freiheitsgrade.

Ein Bild, das Dunkelheit, Screenshot, Schwarz, Raum enthält.

Automatisch generierte Beschreibung

Abb. 5: Drei Punkte auf Ellipse

Nun zeichnen wir die Hyperbel mit den Brennpunkten A und C, welche durch B verläuft (Abb. 6). Den durch B verlaufenden Hyperbelast schneiden wir mit der Ellipse. Schnittpunkt D.

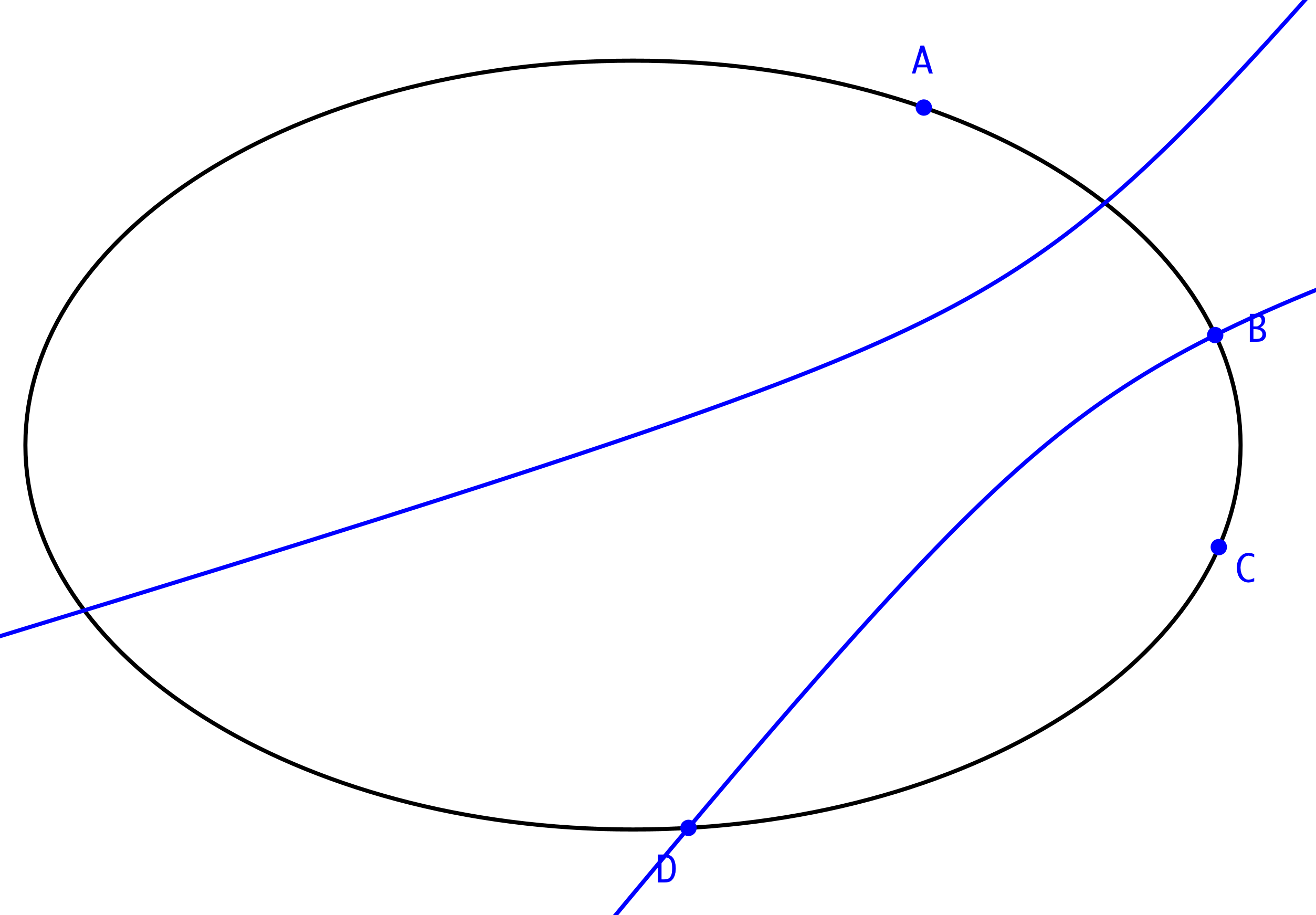
Ein Bild, das Screenshot, Reihe, Raum, Dunkelheit enthält.

Automatisch generierte Beschreibung

Abb. 6: Hyperbel

Das Viereck ABCD ist ein Tangentenviereck (Abb. 7). Dies folgt aus der Abstandseigenschaft der Hyperbel.

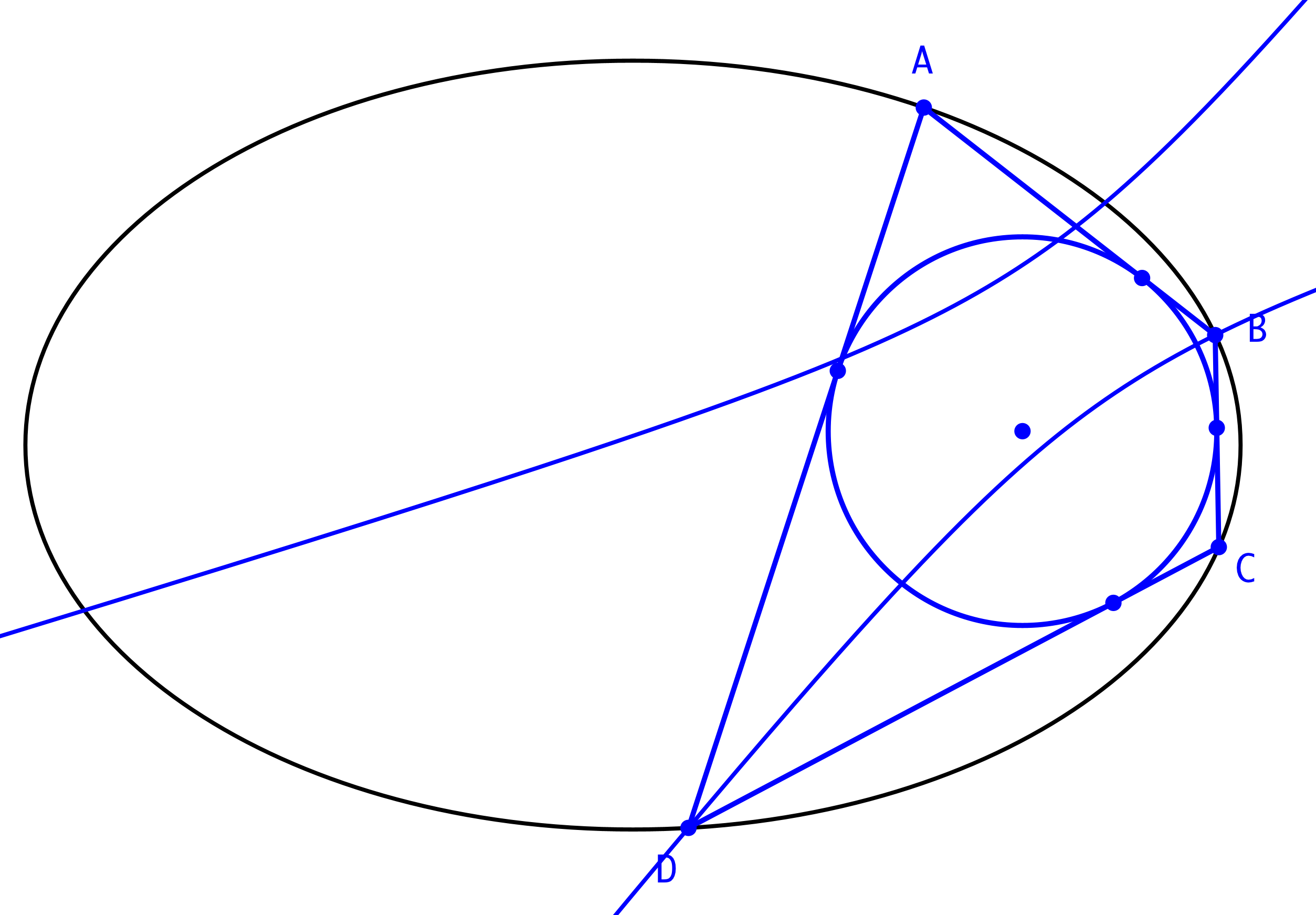
Ein Bild, das Reihe, Screenshot, Kunst, Grafiken enthält.

Automatisch generierte Beschreibung

Abb. 7: Tangentenviereck

Nach dem Satz von Poncelet ergeben sich weitere Lösungen mit demselben Inkreis (Abb. 8).

Abb. 8: Weitere Lösungen

Weblinks

Hans-Jürgen Elschenbroich: Kreis mit Tangentenviereck in Ellipse

https://www.geogebra.org/m/a9kbn4ua

Hans Walser : Tangentenviereck

https://walser-h-m.ch/hans/Miniaturen/T/Tangentenviereck2/Tangentenviereck2.html

Hans Walser: Tangentenviereck

https://walser-h-m.ch/hans/Miniaturen/T/Tangentenviereck/Tangentenviereck.html

Hans Walser: Tangentenviereck als Gelenkmodell

https://walser-h-m.ch/hans/Miniaturen/T/Tang_Viereck_Gelenkmodell/Tang_Viereck_Gelenkmodell.htm

Hans Walser: Tangentenviereck mit Münzen

https://walser-h-m.ch/hans/Miniaturen/T/Tang4eck_m_Muenzen/Tang4eck_m_Muenzen.htm