Hans Walser, [20231122]

Tetraederwelt

1 Worum es geht

Papiermodell eines tetraederförmigen Globus unter Verwendung der Collignon-Projektion

2 Tetraederwelten

Die Abbildung 1 zeigt zwei Modelle. Das Modell links basiert auf hellblauem Druckerpapier, das Modell rechts auf weißem Druckerpapier.

Abb. 1: Tetraederwelten

Die Tetraedermodelle haben keinen Boden, sie sind unten offen (”Hütchen”). Die Modelle können daher gestapelt werden.

Der Nordpol ist in der Tetraederspitze. Der Südpol wird durch die Randlinien des Bodendreieckes repräsentiert.

3 Faltmuster

Die Abbildung 2 zeigt das Faltmuster. Es besteht aus neun gleichseitigen Dreiecken, davon sind drei kartografisch belegt. Der Nordpol ist in der Mitte.

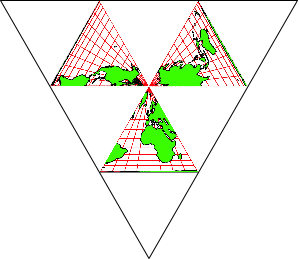
Abb. 2: Faltmuster

Der Anhang enthält ein großes Faltmuster. Das Faltmuster wird ausgedruckt und das große gleichseitige Dreieck ausgeschnitten. Der Ausdruck kann auf weißem oder hellblauem Papier erfolgen. Es genügt die übliche Druckerpapier-Qualität.

4 Faltvorgang

Wir falten zunächst die drei Symmetrieachsen des großen gleichseitigen Dreiecks als Talfalte (Abb. 3).

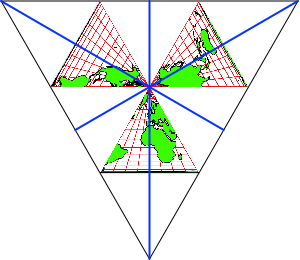
Abb. 3: Symmetrieachsen als Talfalte

Anschließend drehen wir das Papier um und falten die drei Ecken in die Mitte und wieder zurück. Dadurch entstehen auf der Vorderseite drei Bergfalte (Abb. 4). Sie schließen die Kartendreiecke unten ab.

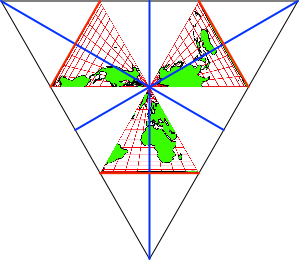
Abb. 4: Bergfalte als Fußlinien der Kartendreiecke

Nun falten wir, ebenfalls auf der Rückseite, die Randlinien des großen Dreiecks auf die eben gefalteten Linien und wieder zurück. Dadurch entstehen auf der Vorderseite drei weitere Bergfalte (Abb. 5). Die Kartendreiecke sind nun vollständig von Bergfalten umgeben.

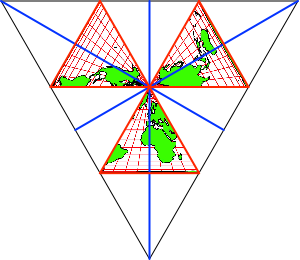
Abb. 5: Weitere Bergfalte

Nun formen wir das Faltmuster zum Tetraeder. Dabei kommt jedes gelb markierte rechtwinklige Dreieck (Abb. 6) auf das benachbarte hellblau markierte zu liegen. Diese Faltlasche legen wir auf der Innenseite des Modells an ein benachbartes Kartendreieck. Abschließend falten wir darüber die grün markierten Dreiecke hinein, so dass ein Hütchen entsteht.

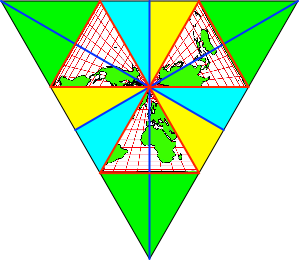
Abb. 6: Abschlussarbeiten

Das Modell ist selbsttragend. Es benötigt keinen Klebstoff und ist reversibel. Man kann es also wieder auseinanderfalten und flach transportieren.

5 Kartografischer Hintergrund

Die Kartendreiecke sind Ausschnitte aus Karten in der Collignon-Projektion. Diese Karten sind flächenverhältnistreu (equal area).

Wir zeigen die Herstellung exemplarisch am Beispiel des Kartendreiecks, das den Nullmeridian (Greenwich) enthält.

Die Abbildung 7 zeigt die Karte in der Collignon-Projektion. Diese Karte hat den Nullmeridian als Symmetrieachse.

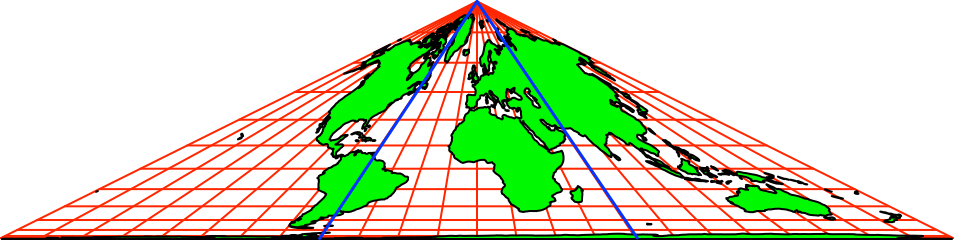
Abb. 7: Collignon-Projektion

Die Karte stellt die gesamte Erdoberfläche dar. Wir benötigen für unser Kartendreieck aber nur einen Drittel davon, aus Symmetriegründen den Teil zwischen 60°W und 60°E. Die Grenzmeridiane sind blau markiert. Die Abbildung 8 zeigt diesen Ausschnitt.

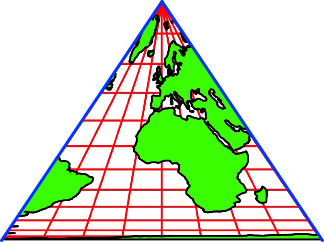
Abb. 8: Benötigter Ausschnitt

Nun ist dieses Dreieck aber nicht gleichseitig, wie das für eine Tetraederseite erforderlich ist. Wir können aber das Dreieck horizontal zusammenpressen, bis es gleichseitig wird (Abb. 9). Dieses Zusammenpressen (eine affine Abbildung) ändert nichts an den Flächenverhältnissen.

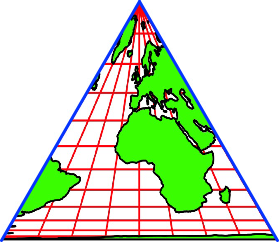
Abb. 9: Gleichseitiges Dreieck

Für die beiden anderen Dreiecke gehen wir analog vor. Die Abbildung 10 zeigt als Beispiel die für den östlichen Teil benötigte Collignon-Karte.

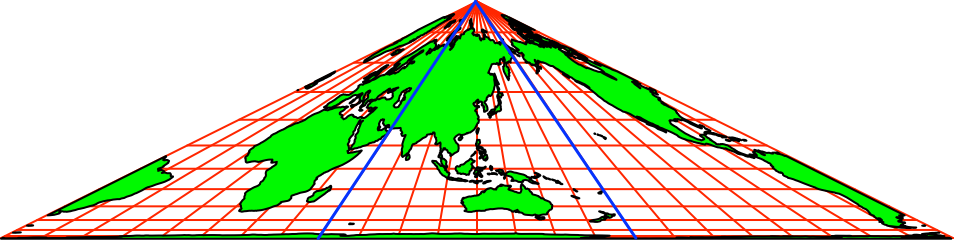
Abb. 10: Asien im Zentrum

6 Flächenverhältnis

Im gleichseitigen Kartendreieck der Abbildung 9 ist der Äquator weit unterhalb der Mitte (Abb. 11).

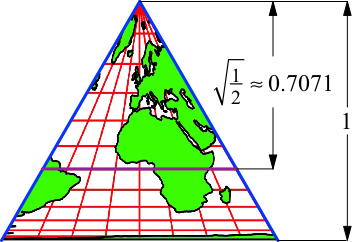
Abb. 11: Position des Äquators

Es handelt sich hier um die klassische Schulaufgabe, ein Dreieck flächenmäßig zu halbieren.

Die Abbildung 12 zeigt die Collignon-Karte der Abbildung 7 zusammen mit den Verzerrungsellipsen. Diese haben zwar unterschiedliche Formen, aber überall den gleichen Flächeninhalt. Daher sind die Flächenverhältnisse invariant.

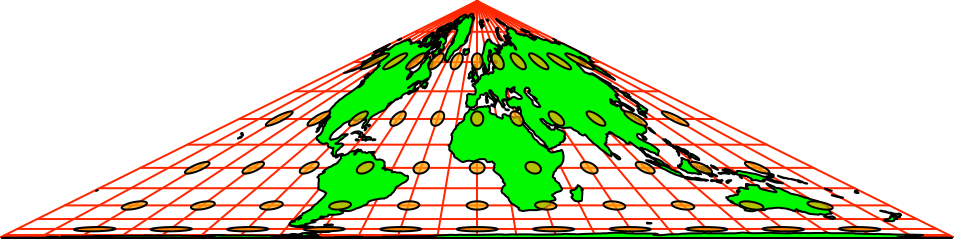
Abb. 12: Verzerrungsellipsen

Anhang

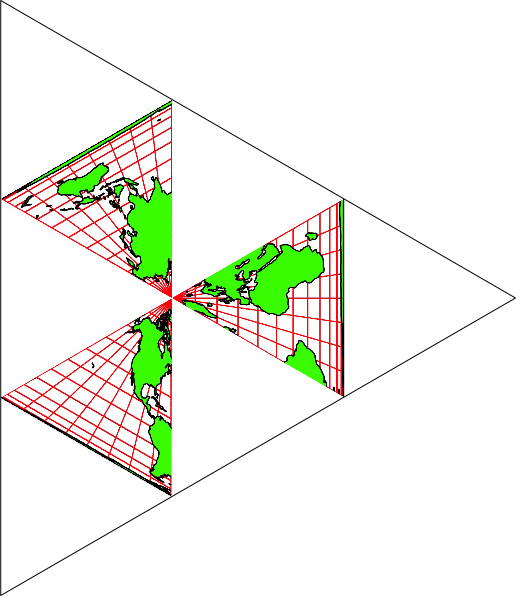
Anhang: Faltmuster

Weblinks

ETH Zurich. Institute of Cartography and Geoinformation (IKG): Kartenprojektionen

https://www.schweizerweltatlas.ch/swatools/MapProjector/MapProjector.de.html

Hans Walser: Collignon

https://walser-h-m.ch/hans/Miniaturen/C/Collignon/Collignon.html

Hans Walser: Quadratwelt

https://walser-h-m.ch/hans/Miniaturen/Q/Quadratwelt/Quadratwelt.html

Hans Walser: Tetraeder-Hütchen

https://walser-h-m.ch/hans/Miniaturen/T/Tetraeder-Huetchen/Tetraeder-Huetchen.htm

Hans Walser: Würfelwelten

https://walser-h-m.ch/hans/Miniaturen/W/Wuerfelwelten/Wuerfelwelten.htm