Hans Walser, [20240224]

Varignon

1 Worum es geht

Zwei verschiedene Beweise zum Satz von Varignon.

2 Erinnerung: Der Satz von Varignon

Die Kantenmitten eines beliebigen Viereckes sind die Ecken eines Parallelogramms (Abb. 1).

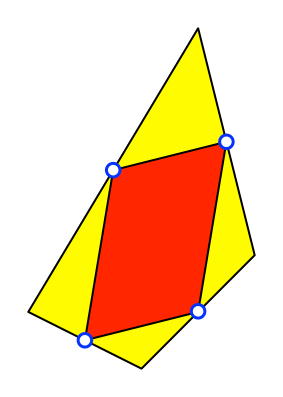
Abb. 1: Satz von Varignon

3 Beweise

3.1 Klassischer Beweis

In der Schule wird in der Regel folgender Beweis zelebriert (Abb. 2): Wir zerschneiden das Viereck mit einer Diagonalen in zwei Teildreiecke. In einem solchen Teildreieckreieck folgt aus dem Strahlensatz, dass die Verbindung der Kantenmitten parallel und halb so lang ist wie die Diagonale.

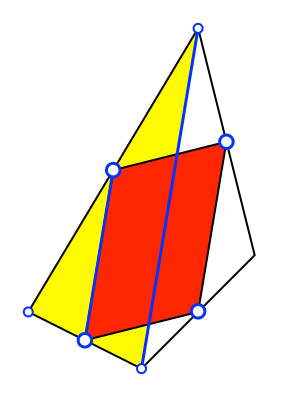
Abb. 2: Strahlensatz

Analog im zweiten Teildreieck (Abb. 3).

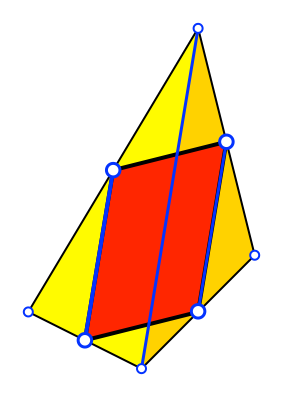
Abb. 3: Zweites Teildreieck

Nun haben wir zwei parallele und gleich lange Strecken. Sie bilden das eine Paar von Parallelseiten eines Parallelogramms. Damit ist der Satz von Varignon bewiesen.

Wir hätten auch mit der anderen Diagonalen wirtschaften können (Abb. 4).

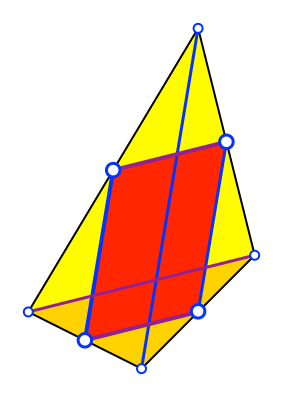
Abb. 4: Andere Diagonale

Die Seiten des Parallelogramms sind halb so lang wie die dazu parallelen Diagonalen des Vierecks.

3.2 Hantel-Beweis

Der Hantel-Beweis basiert auf den Hebelgesetzen von Archimedes.

Wir belegen zwei benachbarte Ecken je mit einer Einheitsmasse und verbinden diese beiden mit einer massenlosen Strecke (Abb. 5). So entsteht eine Hantel.

Abb. 5: Hantel

Der Schwerpunkt dieser Hantel ist ihr Mittelpunkt (Abb. 6). Wir können die beiden Massen in den Ecken ersetzt denken durch eine doppelt so große Masse im Mittelpunkt.

Abb. 6: Mittelpunkt und Schwerpunkt

Analog verfahren wir mit der gegenüberliegenden Kante (Abb. 7).

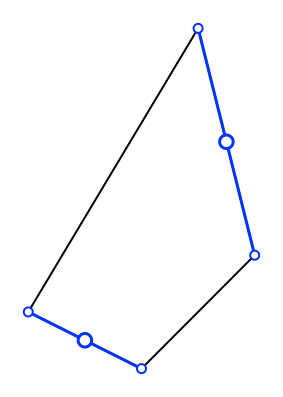
Abb. 7: Gegenüberliegende Kante

Der Schwerpunkt der beiden Kantenschwerpunkte ist wiederum der Mittelpunkt (Abb. 8).

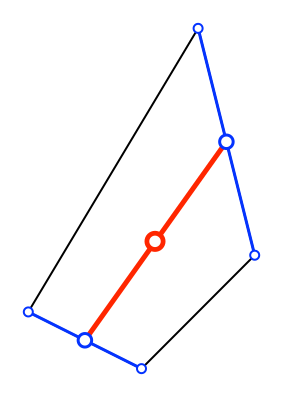
Abb. 8: Schwerpunkt der Kantenschwerpunkte

Dieser Punkt ist auch der Eckenschwerpunkt der vier Vierecks-Ecken. (Rechnerisch: arithmetisches Mittel der Koordinaten der Vierecks-Ecken).

Wenn wir entsprechend mit den beiden anderen Seiten des Viereckes arbeiten, kommen wir ebenfalls zum Eckenschwerpunkt (Abb. 9).

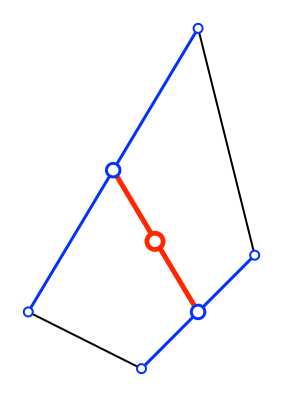
Abb. 9: Andersherum

Die Abbildung 10 zeigt die Überlagerung der beiden Konstruktionen.

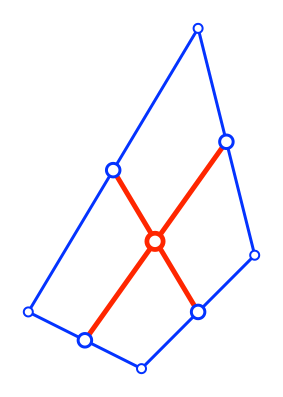
Abb. 10: Überlagerung

Die roten Strecken bilden mit ihren blauen Endpunkten eine punktsymmetrische Figur (Abb. 11). Sie ist das Gerüst (Skelett) eines Parallelogramms (Abb. 12).

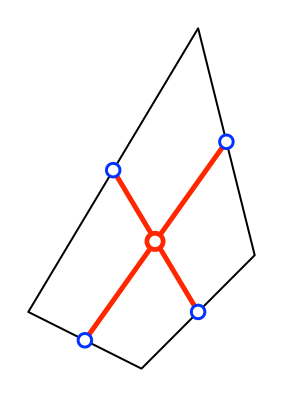
Abb. 11: Punktsymmetrische Figur

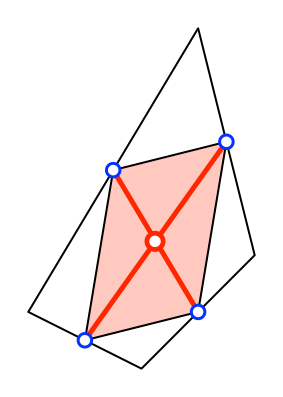
Abb. 12: Parallelogramm

Dieses Parallelogramm ist ebenfalls das Varignon-Parallelogramm.

3.3 Vergleich der beiden Beweise

Der erste Beweis liefert eine Information über die Seitenlängen des Varignon-Parallelogramms (halb so lang wie die Diagonalen des Vierecks).

Aus dem zweiten Beweis ergibt sich, dass der Mittelpunkt des Varignon-Parallelogramms der Eckenschwerpunkt des Viereckes ist.

4 Ein Schmankerl

4.1 Verschiedene Schwerpunkte

Der Eckenschwerpunkt eines Dreiecks ist gleich dem Flächenschwerpunkt dieses Dreieckes. Daher wird oft nur die Terminologie Schwerpunkt verwendet (obwohl der Kantenschwerpunkt des Dreiecks im Allgemeinen ein anderer Punkt ist).

Der Eckenschwerpunkt eines Viereckes ist aber im Allgemeinen nicht der Flächenschwerpunkt dieses Viereckes. Dies kann durch folgendes Gedankenexperiment plausibel gemacht werden: Wir lassen zwei benachbarte Ecken des Viereckes gegeneinander streben. Wir haben dann ein Dreieck, dessen eine Ecke für den Eckenschwerpunkt ein doppeltes Gewicht hat. Für den Flächenschwerpunkt ist aber auch bei dieser Ecke nur mit einfachem Gewicht zu rechnen.

Die Abbildung 13 zeigt den Flächenschwerpunkt (schwarz) für unser Beispiel. (Konstruktionsweg: Mit einer Diagonale in zwei Teildreiecke teilen. In jedem Teildreieck den üblichen Dreiecks-Schwerpunkt. Die beiden Dreiecks-Schwerpunkte verbinden. Analog für die andere Diagonale. Schnittpunkt der beiden Verbindungsgeraden ist der Flächenschwerpunkt des Viereckes).

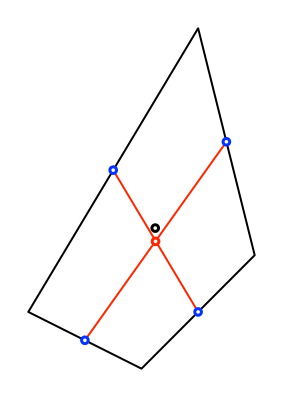
Abb. 13: Flächenschwerpunkt

4.2 Eine Gerade

Wir zeichnen noch die beiden Diagonalen des Viereckes ein (Abb. 14). Der Flächenschwerpunkt (schwarz), der Eckenschwerpunkt (rot) und der Diagonalenschnittpunkt (lila) liegen auf einer Geraden. Der Eckenschwerpunkt teilt die Strecke vom Flächenschwerpunkt zum Diagonalenschnittpunkt im Verhältnis 1:3.

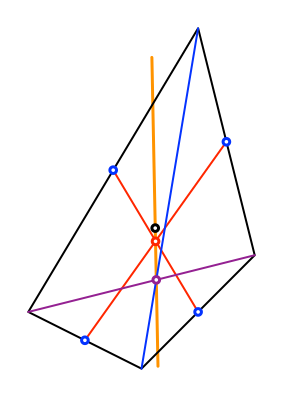
Abb. 14: Eine Gerade

Weblinks

Hans Walser: Varignon

https://walser-h-m.ch/hans/Miniaturen/V/Varignon/Varignon.htm

Hans Walser: Varignon

https://walser-h-m.ch/hans/Miniaturen/V/Varignon2/Varignon2.htm

Hans Walser: Varignon

https://walser-h-m.ch/hans/Miniaturen/V/Varignon3/Varignon3.htm

Hans Walser: Varignon

https://walser-h-m.ch/hans/Miniaturen/V/Varignon4/Varignon4.html