Hans Walser, [20240417]

Wurzelspirale

1 Worum es geht

Kombination von Wurzelrechtecken und der Wurzelspirale

2 Definitionen

Ein Wurzelrechteck hat das Seitenverhältnis √n : 1. Dabei ist n ∈ N eine natürliche Zahl. Ein Wurzelrechteck im Querformat kann in n zueinander kongruente und zum Ausgangsrechteck ähnliche Rechtecke im Hochformat unterteilt werden. Das einfachste Beispiel dazu ist das Quadrat. Das einfachste nicht triviale Beispiel ist ein Rechteck im DIN-Format mit dem Seitenverhältnis √2 : 1.

Die Wurzelspirale ist aus rechtwinkligen Dreiecken mit den Katheten √n und 1 und der Hypotenuse √(n + 1) zusammengesetzt.

3 Kombination

Die Abbildung 1 zeigt die ersten fünf Wurzelrechtecke. Sie sind bereits unterteilt. Dazwischen sind die entsprechenden rechtwinkligen Dreiecke eingeklemmt.

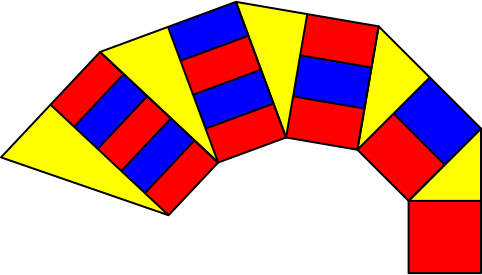
Abb. 1: Fünf Wurzelrechtecke

In den Abbildungen 2 und 3 sehen wir die ersten 25 Wurzelrechtecke. Es ergibt sich ein spiralartiges Verhalten.

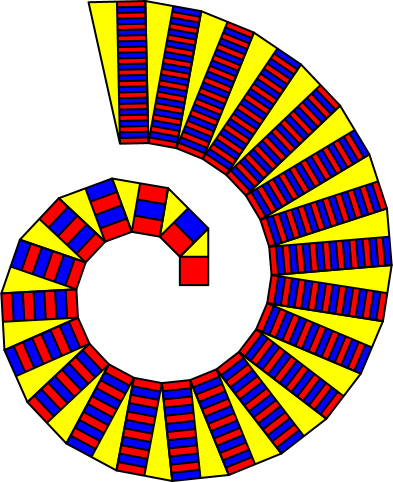
Abb. 2: Spirale

Abb. 3: Aufbau der Spirale

Bei großen Werten von n ergibt sich eine Selbstüberlappung (Abb. 4 für n = 50).

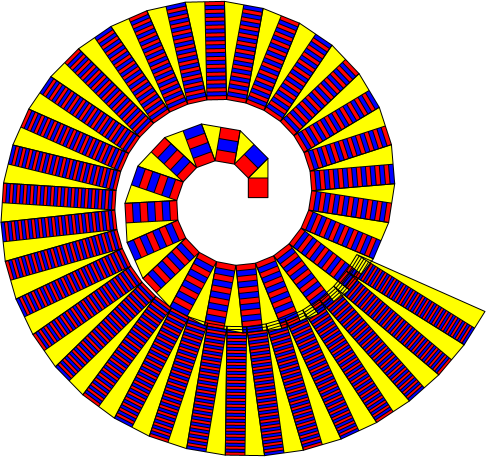
Abb. 4: Selbstüberlappung

4 Durchziehen der Streifen

Das rot-blaue Streifenmuster können wir geradlinig von einem Rechteck auf das nachfolgende Rechteck übertragen (Abb. 5).

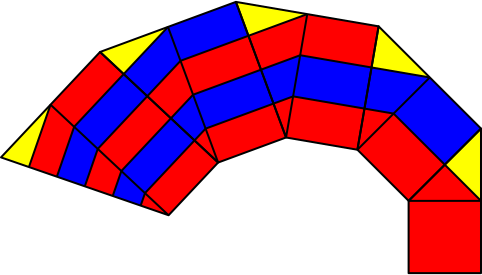
Abb. 5: Übertragung der Streifen

Bei jedem Schritt startet eine weitere rote oder blaue Spirale (Abb. 6 und Abb. 7).

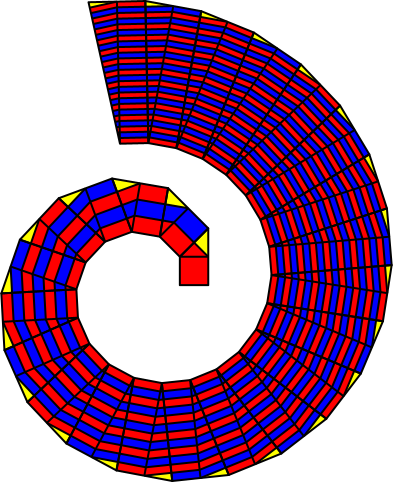
Abb. 6: Rote und blaue Spiralen

Abb. 7: Aufbau der Figur

Weblinks

Hans Walser: Unterteilung durch Falten

https://walser-h-m.ch/hans/Miniaturen/U/Unterteilung_durch_Falten/Unterteilung_durch_Falten.html

Hans Walser: Wurzelpyramide

https://walser-h-m.ch/hans/Miniaturen/W/Wurzelpyramide/Wurzelpyramide.html

Hans Walser: Wurzelrechtecke

https://walser-h-m.ch/hans/Miniaturen/W/Wurzelrechtecke/Wurzelrechtecke.html

Hans Walser: Wurzelspirale

https://walser-h-m.ch/hans/Miniaturen/W/Wurzelspirale/Wurzelspirale.htm

Hans Walser: Wurzelspiralen

https://walser-h-m.ch/hans/Miniaturen/W/Wurzelspiralen/Wurzelspiralen.htm

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).