Hans
Walser, [20240301]
Varignon
Anregung:
Pierre de Varignon, Paris
1 Worum es geht
Verallgemeinerung des Satzes von Varignon
2 Im Quadratraster
Die Abbildung 1 zeigt ein schwarzes Quadratraster mit einem roten Diagonalraster.

Abb. 1: Quadratraster
Wir versuchen nun, diese Figur auf ein allgemeines Viereck zu übertragen.
3 Allgemeines Viereck
Wir unterteilen jede Seite eines allgemeinen Vierecks in gleich viele Teile (acht Teile in Abb. 2).
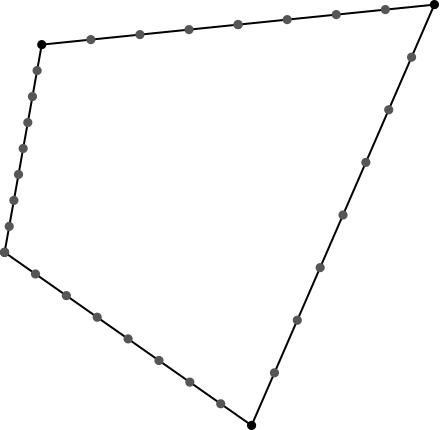
Abb. 2: Allgemeines Viereck mit gleichmäßig unterteilten Seiten
Nun verbinden wir entsprechende Punkte auf gegenüberliegenden Seiten (Abb. 3 und 4).

Abb. 3: Verbindungslinien

Abb. 4: Viereckraster
Wir erhalten ein Viereckraster. Jede Strecke der einen Schar wird von den Strecken der anderen Schar gleichmäßig unterteilt. Dies kann mit Gewichtsüberlegungen gezeigt werden.
Hintergrund: bei der Figur handelt es sich um ein flachgedrücktes hyperbolisches Paraboloid.
4 Diagonalen
Wir zeichnen Diagonalen ein (Abb. 5).
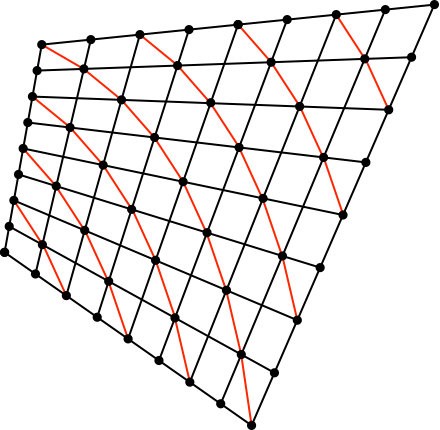
Abb. 5: Diagonalen
Die Stützpunkte einer Diagonalen liegen nicht wie im Quadratraster auf einer Geraden. Sie liegen auf einer Parabel (Abb. 6). Man kann also eine Parabel durch einen linearen Mechanismus in einem allgemeinen Viereck erzeugen.
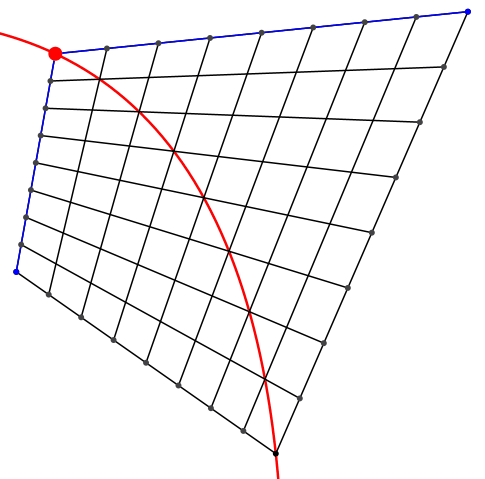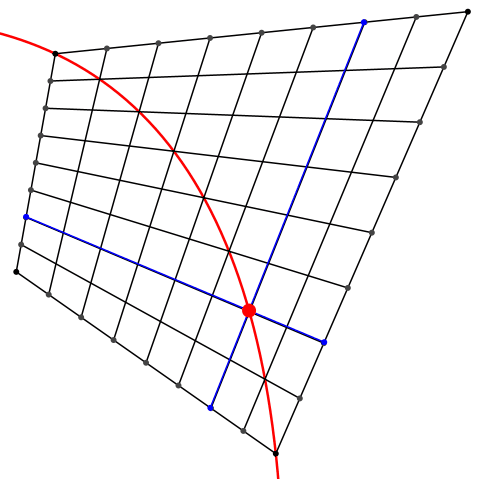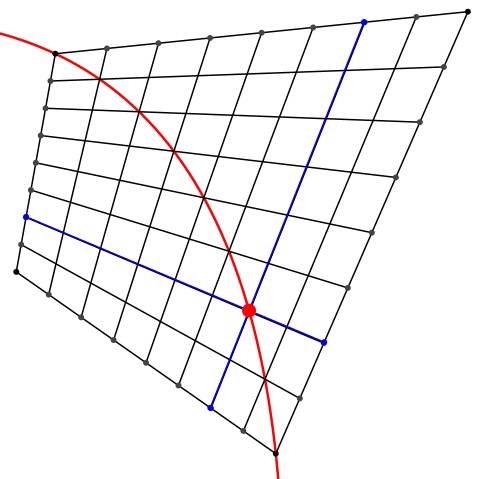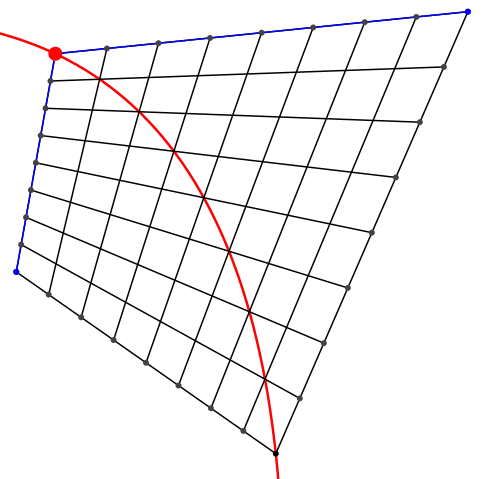
Abb. 6: Parabel
Durch die Konterdiagonalen entsteht ein rotes Viereckraster (Abb. 7).
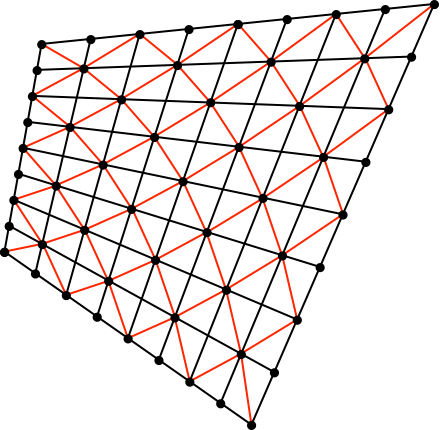
Abb. 7: Viereckraster
Die roten Vierecke sind Parallelogramme. Dies folgt aus dem Satz von Varignon und ist eine Verallgemeinerung davon.
Wenn wir nun von den Kantenmitten des ursprünglichen Viereckes ausgehen, erhalten wir eine Art „Viereck“ (gelb in Abb. 8), dessen gegenüberliegende Seiten stückweise parallel und gleich lang sind, also ein verallgemeinertes „Parallelogramm“.
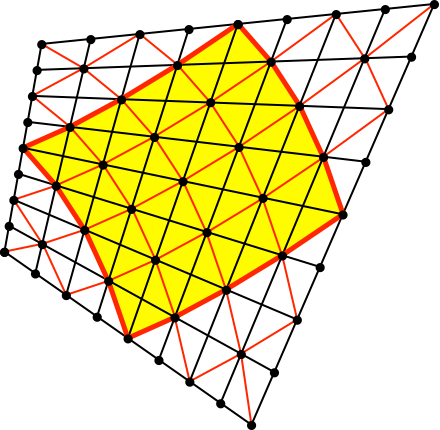
Abb. 8: „Parallelogramm“
5 Parabelscharen
Die Abbildung 9 zeigt die eine der beiden Parabelscharen durch die Gitterpunkte. Die Parabeln sind kongruent und gehen durch Translationen auseinander hervor.
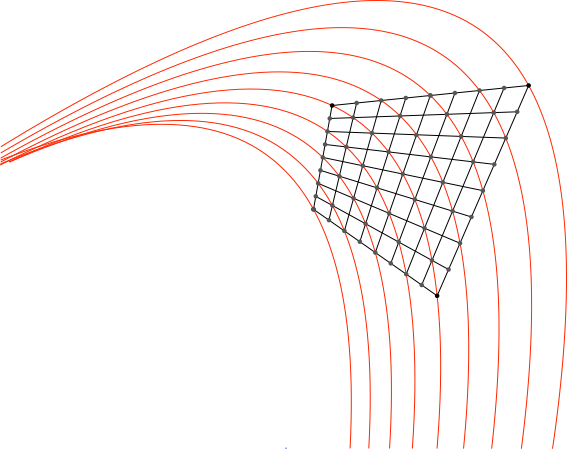
Abb. 9: Parabelschar
In der Abbildung 10 ist auch die zweite Parabelschar eingezeichnet.
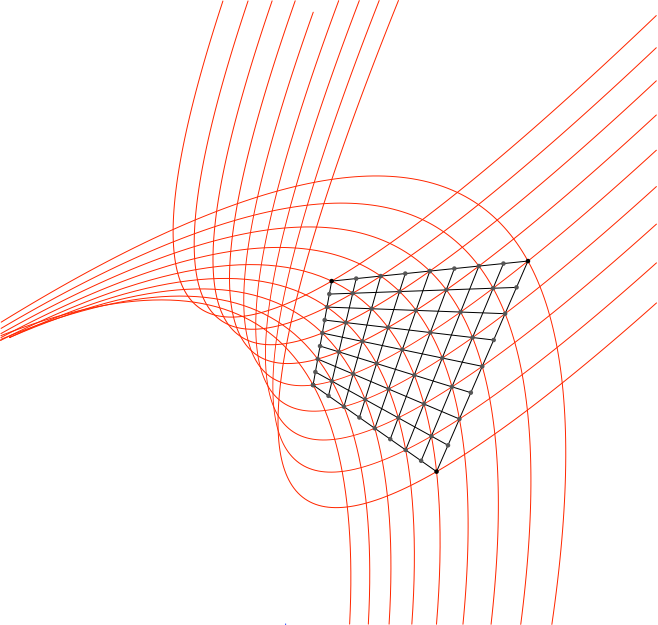
Abb. 10: Zwei Parabelscharen
Zu jedem Schnittpunkt zweier Parabeln gibt es noch einen zweiten Schnittpunkt (Abb. 11).
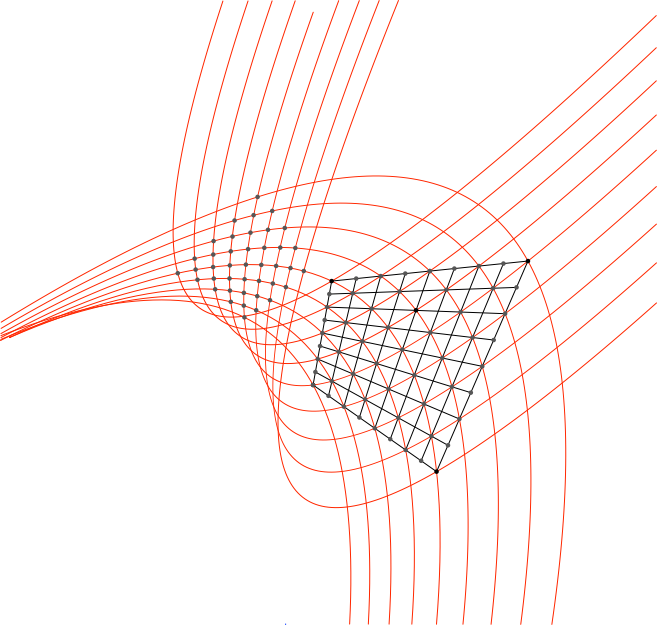
Abb. 11: Zweite Schnittpunkte
Diese zweiten Schnittpunkte liegen nicht mehr auf Geraden, sondern ebenfalls auf Parabeln (Abb. 12).
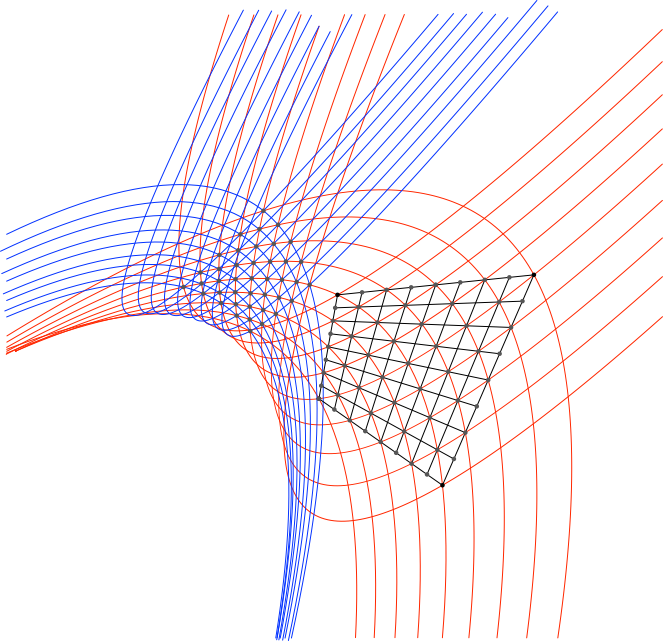
Abb. 12: Weitere Parabeln
Die Parabelscharen umhüllen eine weitere Parabel als Enveloppe. Auch die ursprünglichen schwarzen Geraden tun dies (Abb. 13).
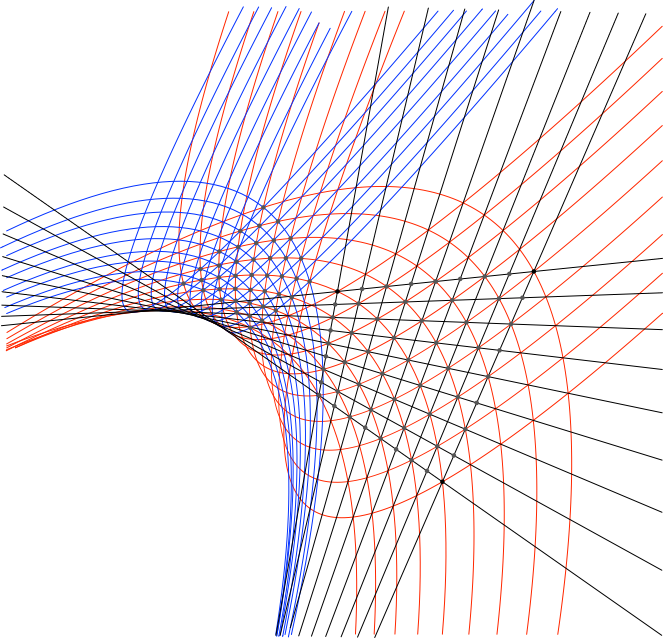
Abb.
13: Enveloppe
Weblinks
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon/Varignon.htm
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon2/Varignon2.htm
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon3/Varignon3.htm
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon4/Varignon4.html
Hans
Walser: Varignon
https://walser-h-m.ch/hans/Miniaturen/V/Varignon5/Varignon5.html