Hans Walser
Dreieck-Origami
Workshop
Österreichische Fortbildungstagung für Geometrie
7. bis 9. November 2024
BIFEB, Bundesinstitut für Erwachsenenbildung
Strobl am Wolfgangsee
Last modified: 02.05.24
1 Worum es geht
Zwei- und dreidimensionale Figuren aus dreieckigem Papier
2 Das dreieckige Papier
2.1 Falten und Schneiden
Wir beginnen mit einem rechteckigen Papier im Querformat (Abb. 1a). Ich habe mit DIN A4 gearbeitet, es geht aber auch mit zum Beispiel US Letter.
Aus didaktischen Gründen wird in den folgenden Figuren angenommen, das Papier sei auf der Vorderseite gelb und auf der Rückseite hellblau. Natürlich können alle Modelle auch mit einfarbigem Papier gebaut werden.
Wir falten die Mittellinie und auf der linken Seite nochmals die Mittellinie (Abb. 1b). Anschließend falten wir zurück.

Abb. 1: Start
Nun falten wir die rechte obere Ecke auf die Mittellinie in der linken Hälfte. Dabei soll die Faltlinie in der Mitte der Oberkante des Papiers beginnen, also am oberen Ende der Mittellinie des Gesamtpapiers (Abb. 2a). So entsteht ein Winkel von 60°.

Abb. 2: Ecke herunterfalten
Das umgefaltete Papierstück schneiden wir ab. Am besten geschieht dies mit einem Taschenmesser oder Papiermesser.
Nun verfahren wir in etwa analog mit der linken oberen Ecke (Abb. 3a) und erhalten nach Abschneiden das gleichseitige Dreieck (Abb. 3b).

Abb. 3: Das gleichseitige Dreieck
Es ist dies das größte gleichseitige Dreieck, das aus dem rechteckigen Papier herausgeschnitten werden kann.
2.2 Symmetrieachsen
Für die meisten Beispiele benötigen wir die drei Symmetrieachsen (Abb. 4), die wir gleich jetzt schon falten. Damit haben wir auch schon den Mittelpunkt des Dreieckes.

Abb. 4: Symmetrieachsen
Ein kleiner Schönheitsfehler ist das Reststück der Faltlinie links. Diese war zur Konstruktion des 60°-Winkels erforderlich, wird aber im Folgenden nicht mehr gebraucht. Die Lage dieses Reststückes ist durch das Format des Papier-Rechteckes bedingt und hat keine geometrische Bedeutung im gleichseitigen Dreieck. In vielen Modellen kommt dieses Reststück ins Innere des Modells zu liegen und ist dann nicht mehr sichtbar. Dieses Reststück wird daher in den folgenden Faltanleitungen nicht mehr gezeigt.
2.3 Resteverwertung
Die Abbildung 5 zeigt, wie aus dem Reststück rechts oben ein weiteres, kleineres gleichseitiges Dreieck gewonnen werden kann.

Abb. 5: Resteverwertung
Es bleibt wieder ein Reststück übrig. Aus diesem kann durch Falten und Schneiden wiederum ein gleichseitiges Dreieck gewonnen werden, oder aber auch ein regelmäßiges Sechseck. Ausprobieren!
3 Stern
Wir falten eine Dreiecksecke auf den Mittelpunkt der gegenüberliegenden Dreiecksseite (Abb. 6a) und wieder zurück. Diesen Vorgang wiederholen wir für die beiden anderen Ecken (Abb. 6b).
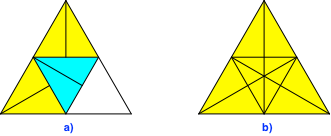
Abb. 6: Ecken auf Seitenmitten
Nun wenden wir um und falten auf der Rückseite jede Ecke in den Mittelpunkt des Dreiecks und wieder zurück (Abb. 7).
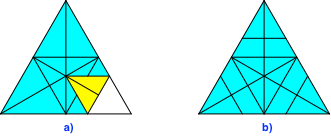
Abb. 7: Ecken auf Mittelpunkt
Wir wenden zurück und falten auf der Vorderseite eine Ecke mit der langen Faltlinie hinein und dann mit der kurzen Faltlinie wieder hinaus (Abb. 8a). Wir wiederholen den Vorgang mit einer zweiten Ecke (Abb. 8b). Dabei falten wir über die erste eingefaltete Ecke.
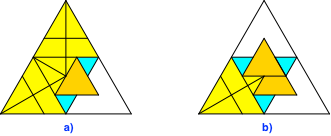
Abb. 8: Doppelfaltung
Bei der dritten Ecke falten wir über die zweite Ecke, schieben aber den Anfang sorgfältig unter die erste Ecke (Abb. 9a). Dadurch entsteht eine zyklische Hackordnung: Jede Faltung ist oberhalb der vorhergehenden und unterhalb der nachfolgenden. Diese zyklische Hackordnung garantiert den Zusammenhang des Stern-Modells (Abb. 9b und Abb. 10) ohne Leim oder andere Bindemittel.

Abb. 9: Dritte Doppelfaltung

Abb. 10: Stern aus einem Dreieck-Origami-Papier
4 Zweifarbiger Stern
Für dieses Modell benötigen wir zwei Dreieck-Origami-Papiere, vorzugsweise in verschiedenen Farben. Beide werden genau gleich gefaltet.
Zunächst falten wir auf der Rückseite die drei Ecken in die Mitte (Abb. 11).

Abb. 11: Ecken in die Mitte falten
Wir wenden auf die Vorderseite (Abb. 12a). Dann falten wir die unterste Kante in die Mitte (Abb. 12b). Anschließend falten wir die Kante rechts oben in die Mitte, und zwar über die von unten heraufgefaltete Kante (Abb. 12c).

Abb. 12: Kanten in die Mitte falten
Und nun kommt wieder der Trick mit der zyklischen Hackordnung: die Kante von links oben kommt über die Kante von rechts oben zu liegen, aber unter die Kante von unten (Abb. 13a). Dadurch wird die Figur stabil.
Durch Umwenden ergibt sich ein Dreieck mit je einem von jeder Ecke ausgehenden Rhombus.
Das zweite Dreieck-Origami-Papier falten wir genau gleich. Wir können nun das eine Dreieck unter die Rhomben des anderen platzieren. Ist ein bisschen heikel, geht aber. Die Rhomben halten klauenartig von drei Seiten her das eingefügte Dreieck. Somit haben wir den zweifarbigen Stern (Abb. 13c und Abb. 14).

Abb. 13: Abschluss

Abb. 14: Zweifarbiger Stern
5 Tetraeder-Hütchen
Wir bauen ein unten offenes Tetraeder aus einem Dreieck-Origami-Papier.
Zunächst falten wir die drei Ecken in die Mitte und wieder zurück (Abb. 15).

Abb. 15: Ecken in die Mitte und wieder zurück
Dann falten wir die drei Dreiecksseiten auf die eben entstandenen parallelen Faltkanten und zurück (Abb. 16).
Nun wenden wir das Origami-Papier und falten auf der Rückseite genau dasselbe Faltprogramm. Dadurch wird jede Faltlinie zweigängig verwendbar.
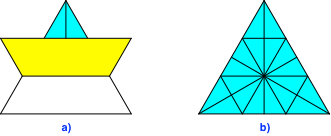
Abb. 16: Parallele Faltlinien
In der Abbildung 17a ist die Unterteilung des Origami-Dreiecks aus Kognitionsgründen (das heißt, damit man es besser versteht) neu gefärbt. Die drei orange gefärbten Dreiecke werden zu den drei Außenseiten des Tetraeder-Hütchens. Das jeweils benachbarte grüne und magenta rechtwinklige Dreieck werden aufeinandergelegt und auf der Innenseite auf das dem magenta-Dreieck benachbarte orange Dreieck gelegt. Dann wird das dem orangen Dreieck benachbarte hellorange Dreieck nach innen geklappt, also über das grüne und dass magenta Dreieck. Die Abbildung 17b zeigt die fast fertige Situation. Es muss noch das letzte hellorange Dreieck hineingeklappt werden. Das Modell hält ohne Leim.
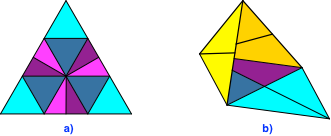
Abb. 17: Neue Färbung und Aufbau des Modells
Die Abbildungen 18 und 19 zeigen ein reales Modell.

Abb. 18: Papiermodell

Abb. 19: Fehlender Boden
6 Tetraederwelt
Die Abbildung 20 zeigt ein gleichseitiges Dreieck, das mit einer aus drei kleinen gleichseitigen Dreiecken zusammengesetzten Weltkarte bestückt ist.

Abb. 20: Weltkarte
Das Dreieck kann ausgedruckt (zum Besispiel auf hellblaues Papier) und ausgeschnitten und zu einem Tetraeder-Hütchen verarbeitet werden. Dies ergibt eine Tetraederwelt (Abb. 21). Der Nordpol ist in der Spitze des Tetraederhütchens, der Südpol in den Kanten des Bodendreiecks (Abb. 22).

Abb. 21: Tetraederwelt

Abb. 22: Blick auf den Südpol
Kartografisch handelt es sich um die Collignon-Projektion. Diese ist flächenverhältnistreu, die Flächenverhältnisse sind also auf den drei Mantelflächen des Tetraeders gleichwie auf der Erdkugel.
7 Origami-Oktaeder
Das Origami-Oktaeder besteht aus zweimal vier Bauteilen, vorzugsweise in zwei verschiedenen Farben. In den folgenden Abbildungen wurden aber aus didaktischen Gründen immer die Farben gelb für Vorderseite und Hellblau für Rückseite verwendet.
7.1 Bauteil Typ 1
Für den Bauteil vom Typ 1 falten wir auf der Rückseite jede Ecke in die gegenüberliegende Seitenmitte und zurück (Abb. 23).

Abb. 23: Falten auf der Rückseite
Dann wenden wir um und falten auf der Vorderseite die Ecken in die im Uhrzeigersinn anschließende Seitenmitte (Abb. 24 und 25). Wir haben also außen doppellagige rechtwinklige Dreiecke.
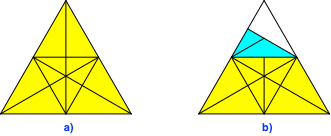
Abb. 24: Falten auf der Vorderseite

Abb. 25: Falten auf der Vorderseite. Fortsetzung
Nun wenden wir wieder um. Nun ist also die Rückseite wieder oben (Abb. 26a). Wir falten ein erstes doppellagiges rechtwinkliges Dreieck hinein (Abb. 26b).

Abb. 26: Hineinfalten
Nun falten wir analog das im Gegenuhrzeigersinn anschließende doppellagige rechtwinklige Dreieck über das erste hinein (Abb. 27b). Dann wird das dritte doppellagige rechtwinklige Dreieck so hineingefaltet, dass es über das zweite, aber unter das erste zu liegen kommt (Abb. 27b). Wir generieren somit wiederum eine zyklische Hackordnung, welche das Modell stabilisiert. Dies gibt dann ein Bauteil vom Typ 1.

Abb. 27: Zyklische Hackordnung
An den Außenkanten des Bauteils vom Typ 1 haben wir Schlitze, unter denen sich Taschen in Form und Größe der rechtwinkligen Dreiecke befinden.
Die Abbildung 28 zeigt links ein Bauteil vom Typ 1. Deutlich erkennen wir die zyklische Hackordnung. Die Bauteile sind von der Rückseite her abgebildet, also von der Innenseite des fertigen Modells.

Abb. 28: Bauteile vom Typ 1 und 2
7.2 Bauteil Typ 2
Für den Bauteil vom Typ 2 falten wir ebenfalls auf der Rückseite jede Ecke in die gegenüberliegende Seitenmitte und zurück (Abb. 29).
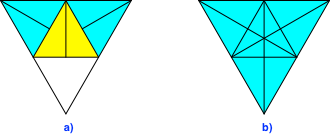
Abb. 29: Falten auf der Rückseite
Anschließend falten wir, immer noch auf der Rückseite, die Ecken auf die im Uhrzeigersinn anschließenden Seitenmitten (Abb. 30). Dies gibt dann ein Bauteil vom Typ 2.

Abb. 30: Rechtwinklige Dreiecke
Die Abbildung 28 zeigt rechts ein Bauteil vom Typ 2.
7.3 Zusammensetzen des Oktaeders
Ein Bauteil vom Typ 2 kann nun in einen Schlitz eines Bauteils vom Typ 1 eingeschoben werden (Abb. 28, 31 und 32).

Abb. 31: Einschieben des Bauteils vom Typ 2 in ein Bauteil vom Typ 1

Abb. 32: Zusammengeschobene Bauteile
Die Abbildung 33 zeigt die zusammengeschobenen Bauteile von der Außenseite des fertigen Modells.

Abb. 33: Außenseite
Für das Oktaeder benötigen wir acht Bauteile, vier von jedem Typ. Wir können mit zwei verschiedenen Farben arbeiten, der Autor hat, wie man sieht, für die Bauteile vom Typ1 hellblaues Papier verwendet und rosa Papier für die Bauteile vom Typ 2.
Die Abbildung 34 zeigt das fertige Modell.

Abb. 34: Origami-Oktaeder
8 Oktederwelt
Die Abbildung 35 zeigt die acht Vorlagen für die Bauteile einer Oktaederwelt. In der Abbildung 37 sind sie in größerem Format für das Ausdrucken gegeben. Die schwarzen Dreiecke werden ausgedruckt und ausgeschnitten und zu den einzelnen Bauteilen gefaltet. Beim Falten müssen wir benachbarte Dreiecke im Wechsel gemäß Typ 1 beziehungsweise Typ 2 falten.

Abb. 35: Vorlagen für die Bauteile
Die Abbildung 36 zeigt die zugehörige Oktaederwelt. Kartograifsch handelt es sich wiederum um Collignon-Projektionen.

Abb. 36: Oktaederwelt
Die Abbildung 37 gibt acht Vorlagen in größerem Format. Es wird jeweils die geografische Länge des mittleren Meridians angegeben.
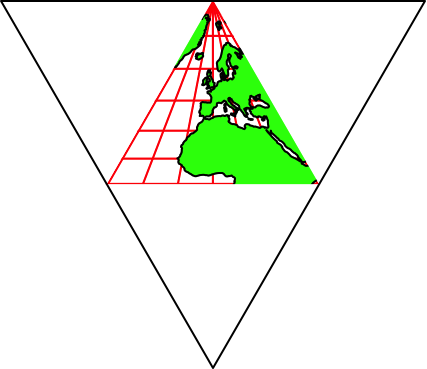
Abb. 37.1: 0°-Meridian. Nord
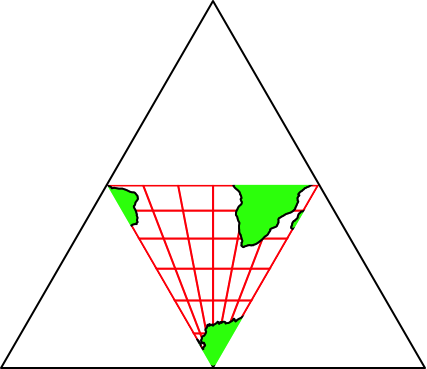
Abb. 37.2: 0°-Meridian. Süd
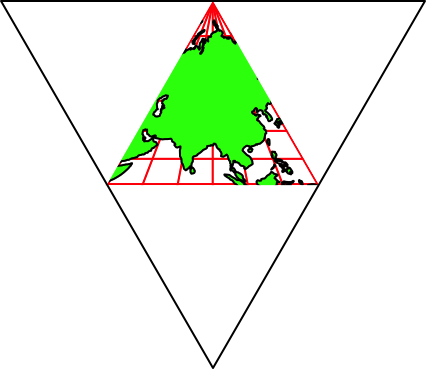
Abb. 37.3: 90°-Meridian. Nord
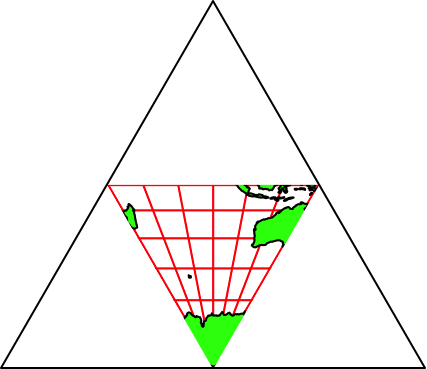
Abb. 37.4: 90°-Meridian. Süd
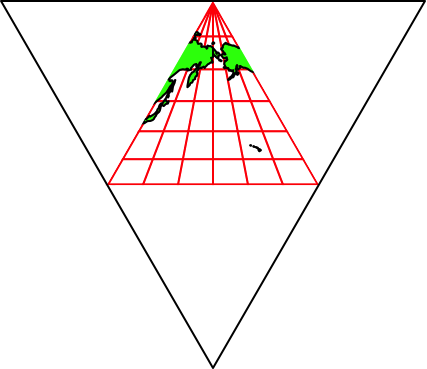
Abb. 37.5: 180°-Meridian. Nord

Abb. 37.6: 180°-Meridian. Süd

Abb. 37.7: 270°-Meridian. Nord
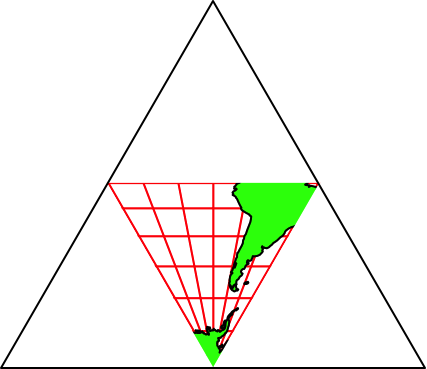
Abb. 37.8: 270°-Meridian. Süd
Weblinks
ETH Zurich. Institute of Cartography and
Geoinformation (IKG): Kartenprojektionen
https://www.schweizerweltatlas.ch/swatools/MapProjector/MapProjector.de.html
Hans
Walser: Collignon
https://walser-h-m.ch/hans/Miniaturen/C/Collignon/Collignon.html
Hans
Walser: Dreieck-Origami
https://walser-h-m.ch/hans/Miniaturen/D/Dreieck-Origami/Dreieck-Origami.htm
Hans Walser: Oktaeder-Welt
https://walser-h-m.ch/hans/Miniaturen/O/Oktaeder-Welt/Oktaeder-Welt.html
Hans Walser: Origmai-Oktaeder
https://walser-h-m.ch/hans/Miniaturen/O/Origami-Oktaeder/Origami-Oktaeder.html
Hans Walser: Tetraeder-Hütchen
https://walser-h-m.ch/hans/Miniaturen/T/Tetraeder-Huetchen/Tetraeder-Huetchen.htm
Hans Walser: Tetraederwelt
https://walser-h-m.ch/hans/Miniaturen/T/Tetraederwelt/Tetraederwelt.html