1 Worum es geht

Einschiebekonstruktion für das regelmäßige Siebeneck mit einer Sinuskurve

Einblick in die Sinusfunktion

Einfluss der Kreisfrequenz

2 Konstruktionsvorgang

Die Abbildung 1 zeigt den kinematischen Konstruktionsvorgang.

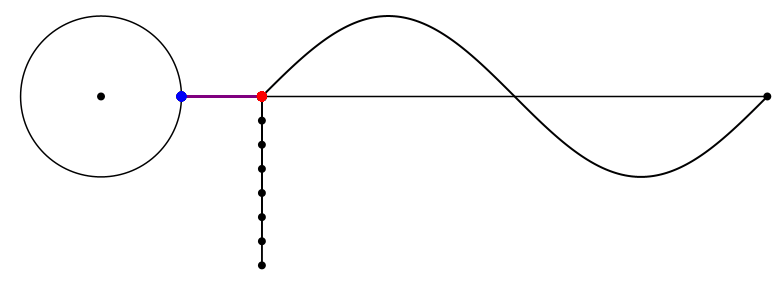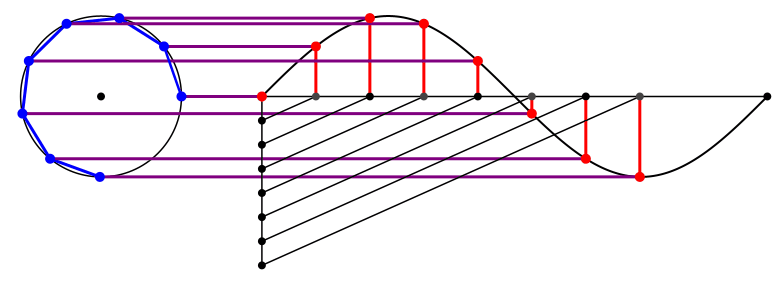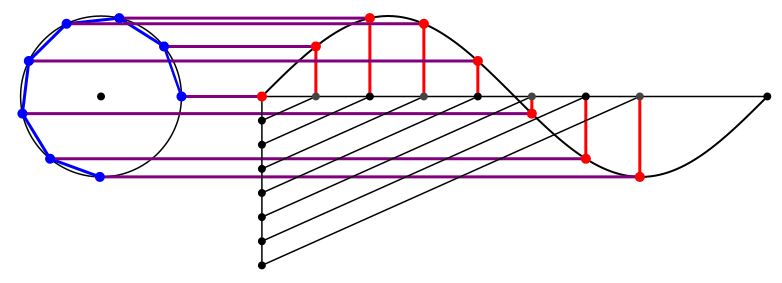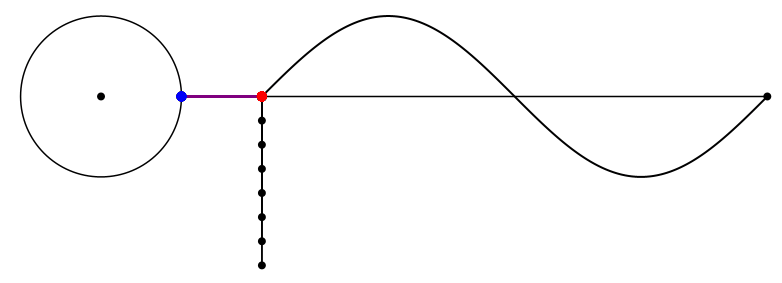
Abb. 1: Kinematik

In der Endlage (Abb. 2) erhalten wir ein regelmäßiges Siebeneck.

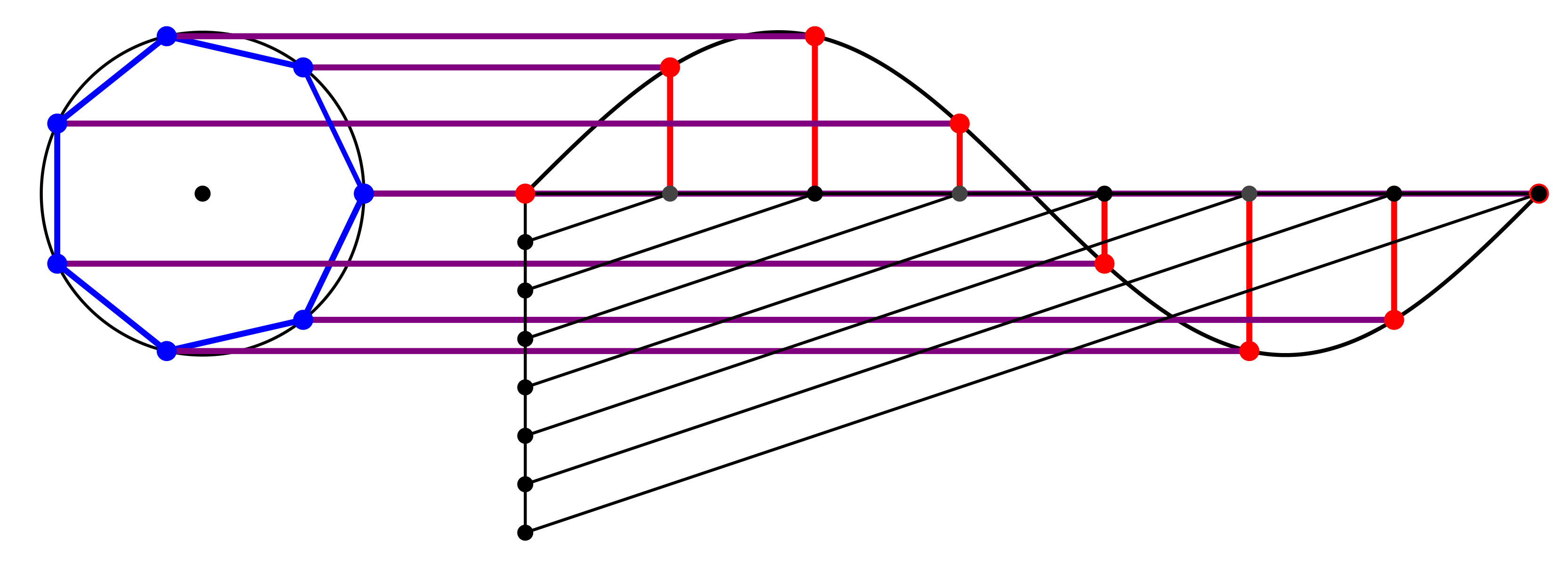
Ein Bild, das Reihe, Screenshot, Diagramm, Farbigkeit enthält.

Automatisch generierte Beschreibung

Abb. 2: Endlage

Bemerkung: Wir könnten auch direkt die Periodenlänge der Sinuskurve durch 7 teilen. Der kinematische Einschiebeprozess ist eigentlich überflüssig aber lustig.

3 Größere Kreisfrequenzen

Im Beispiel der Abbildungen 1 und 2 ist die Kreisfrequenz gleich 1.

Wir erhöhen nun die Kreisfrequenz.

Die Abbildungen 3 und 4 zeigen die Situation für die Kreisfrequenz 2.

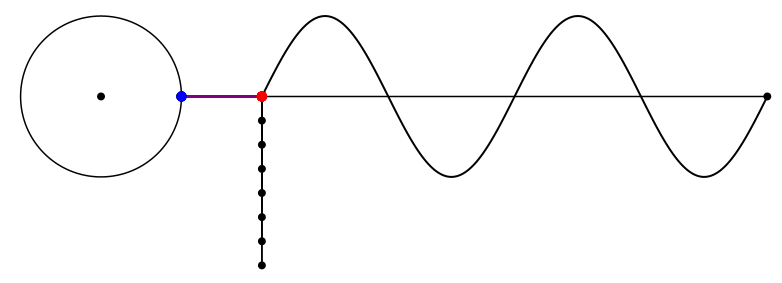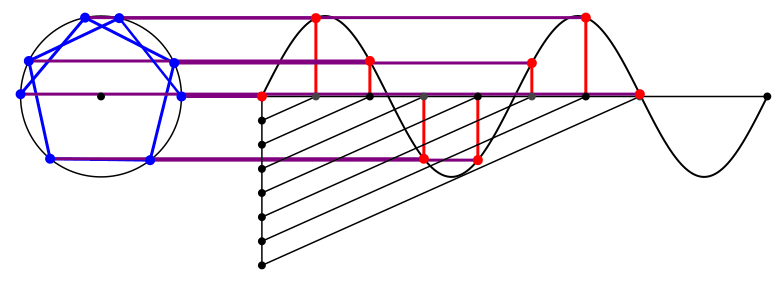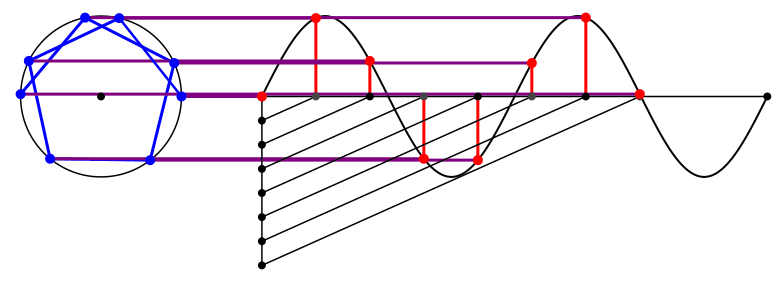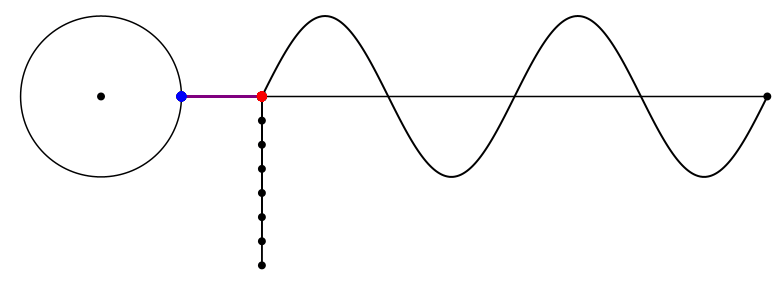
Abb. 3: Kreisfrequenz 2

In der Endlage (Abb. 4) ergibt sich der Diagonalenstern mit den kürzeren Diagonalen.

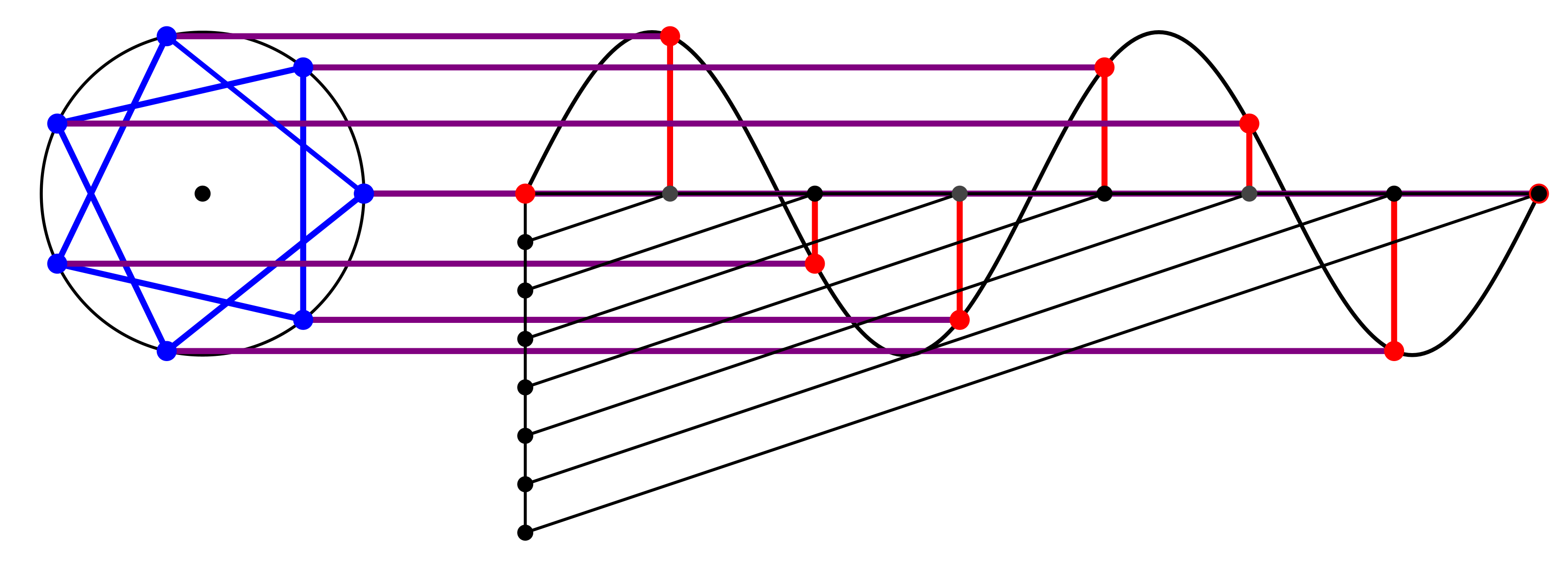
Abb. 4: Diagonalenstern

Für die Kreisfrequenz 3 ergibt sich der Diagonalenstern mit den längeren Diagonalen (Abb. 5 und Abb. 6).

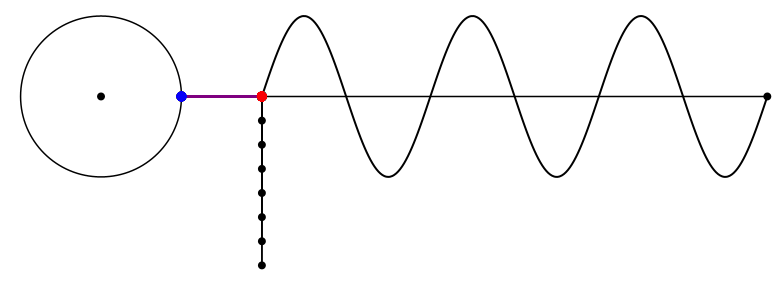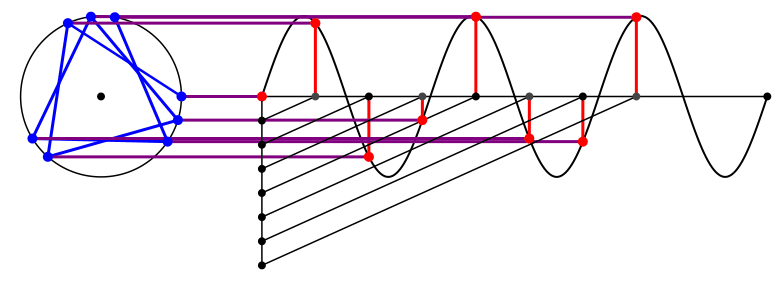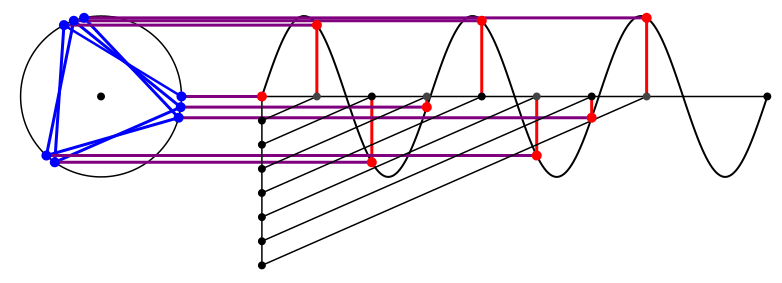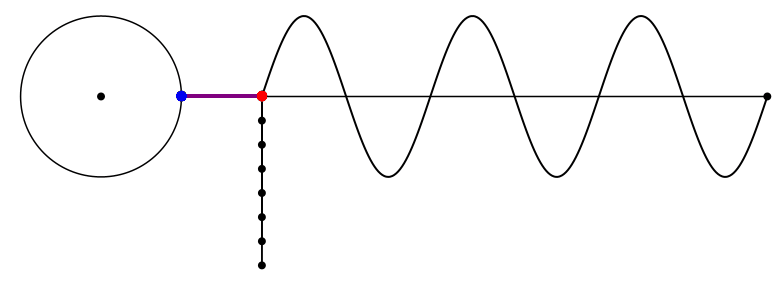
Abb. 5: Kreisfrequenz 3

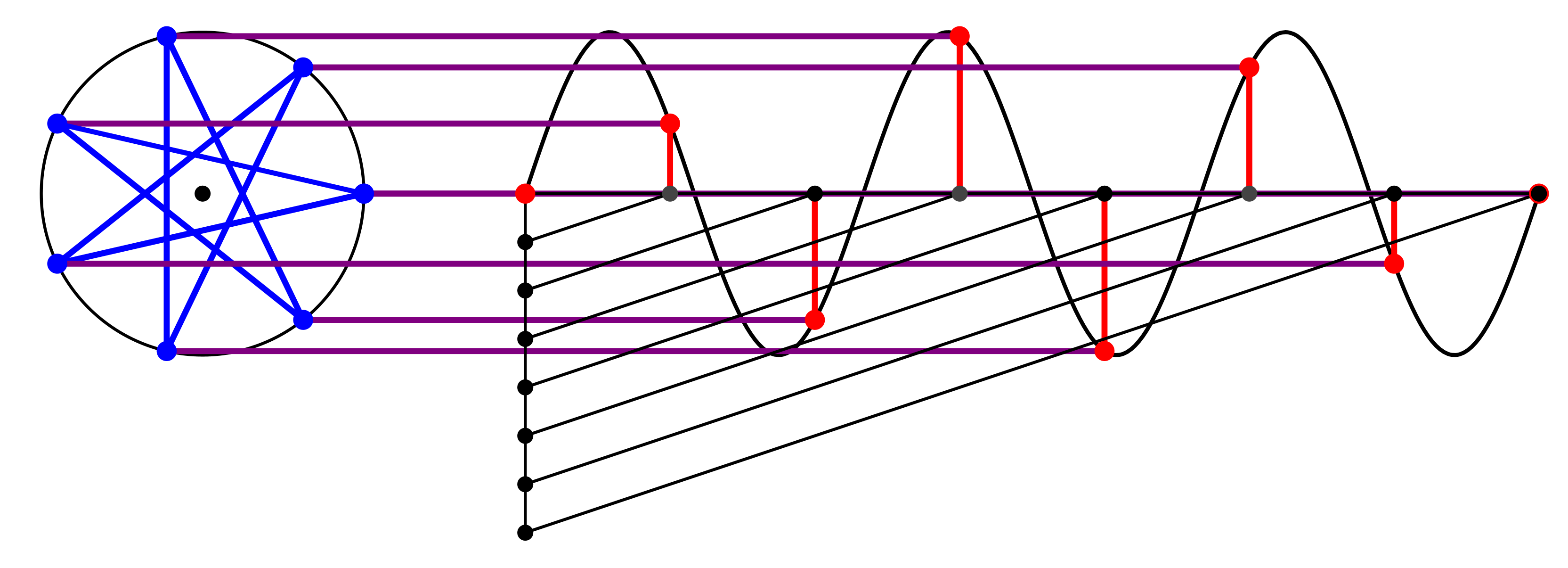
Ein Bild, das Reihe, Screenshot, Farbigkeit, Diagramm enthält.

Automatisch generierte Beschreibung

Abb. 6: Diagonalenstern mit großen Diagonalen

Bei der Kreisfrequenz 4 ergibt sich auch der Diagonalenstern mit den längeren Diagonalen (Abb. 7 und Abb. 8). Es wird aber „überdreht“.

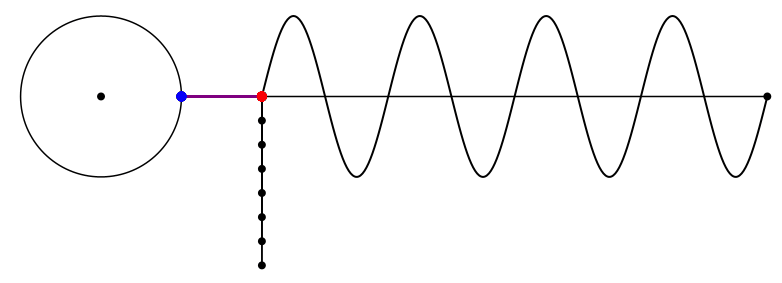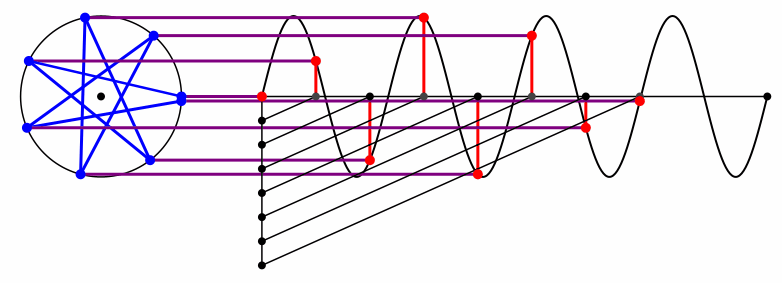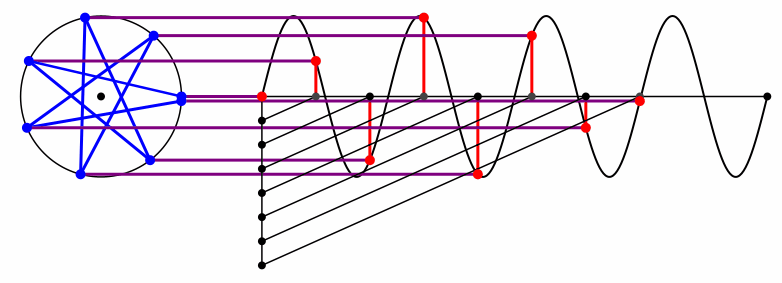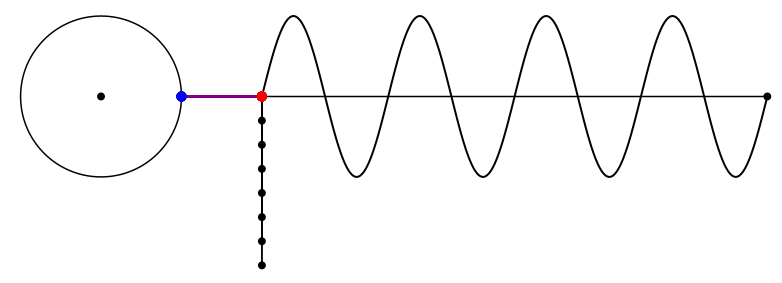
Abb. 7: Kreisfrequenz 4

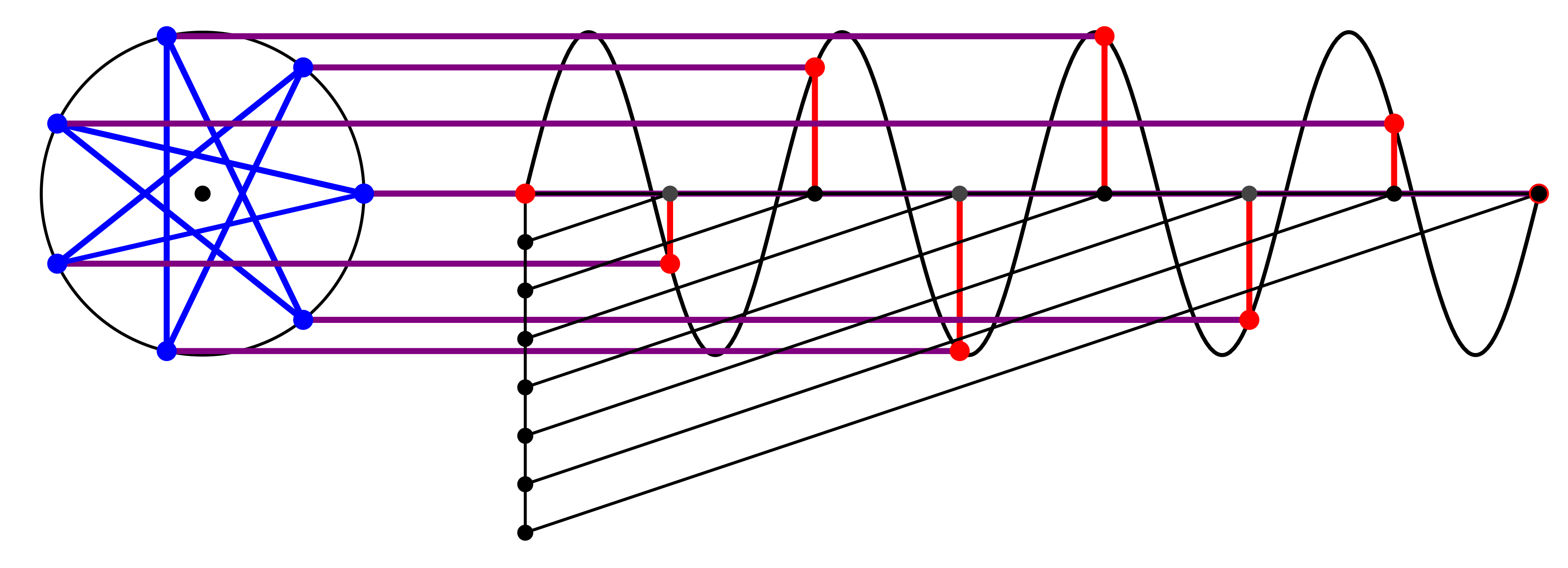
Ein Bild, das Reihe, Screenshot, Farbigkeit, Diagramm enthält.

Automatisch generierte Beschreibung

Abb. 8: Endlage

Bei der Kreisfrequenz 5 ergibt sich „nur“ der Diagonalenstern mit den kürzeren Diagonalen (Abb. 9 und Abb. 10).

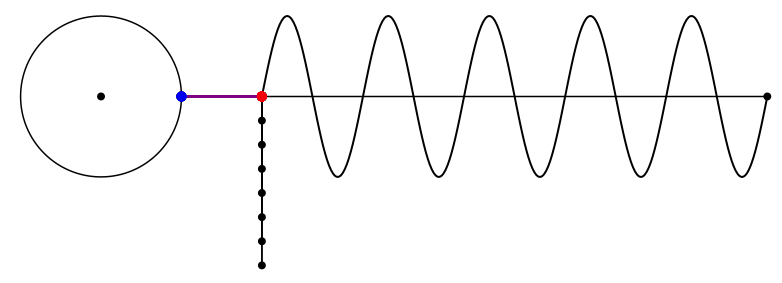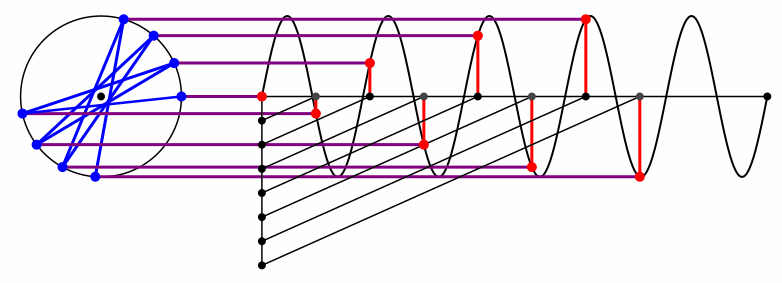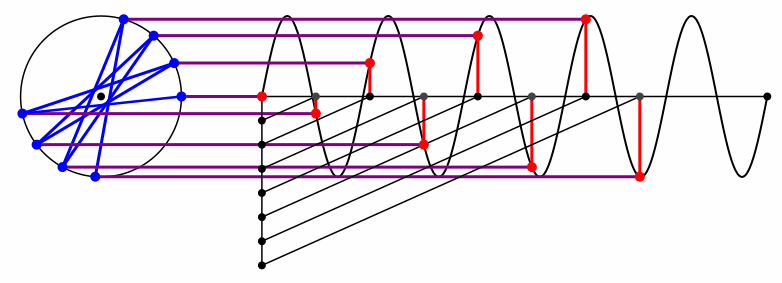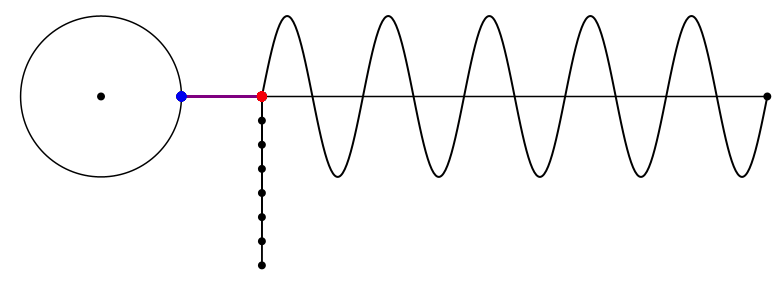
Abb. 9: Kreisfrequenz 5

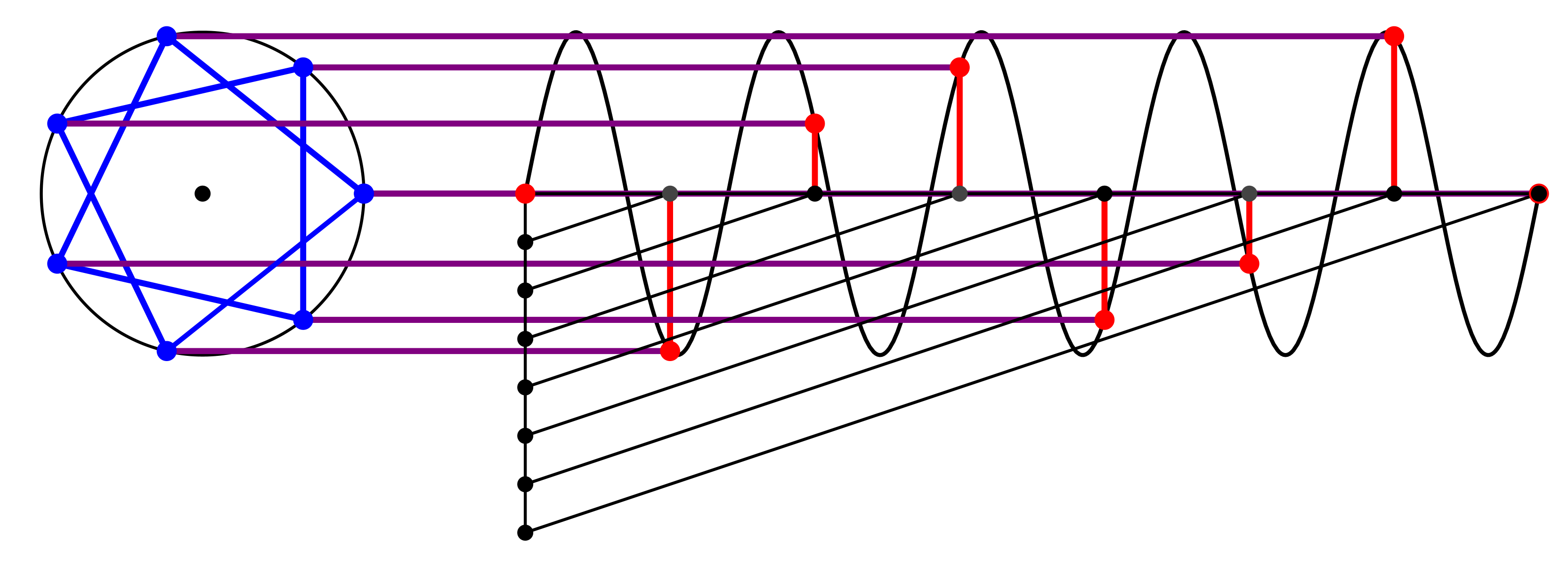
Ein Bild, das Reihe, Screenshot, Farbigkeit, Diagramm enthält.

Automatisch generierte Beschreibung

Abb. 10: Endlage

Bei der Kreisfrequenz 6 kommen wir zum regelmäßigen Siebeneck zurück (Abb. 11 und Abb. 12). Allerdings ist der Orientierungssinn umgekehrt im Vergleich zum ersten Siebeneck.

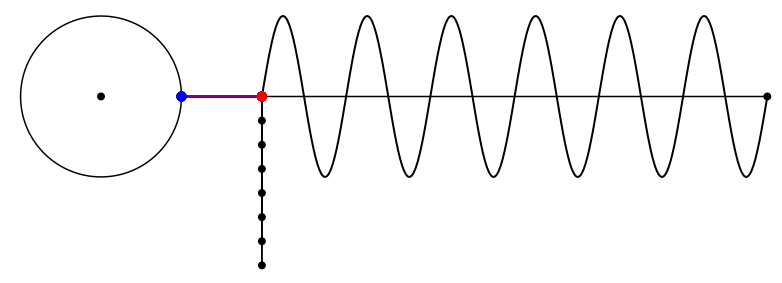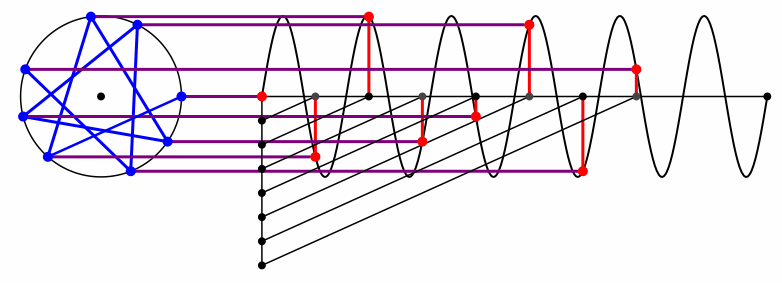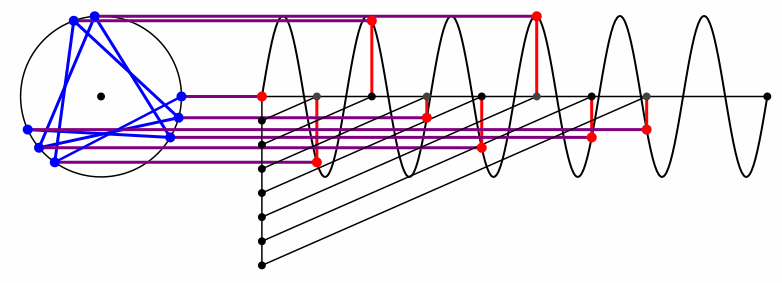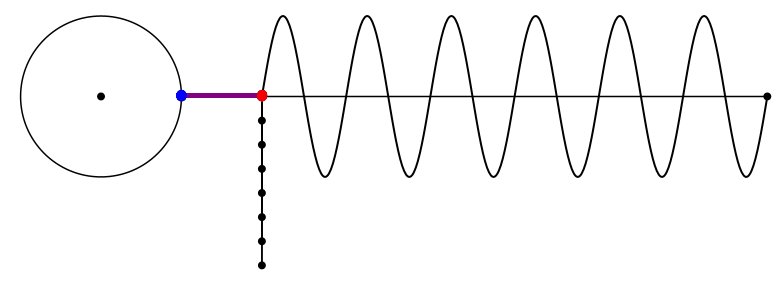
Abb. 11: Kreisfrequenz 6

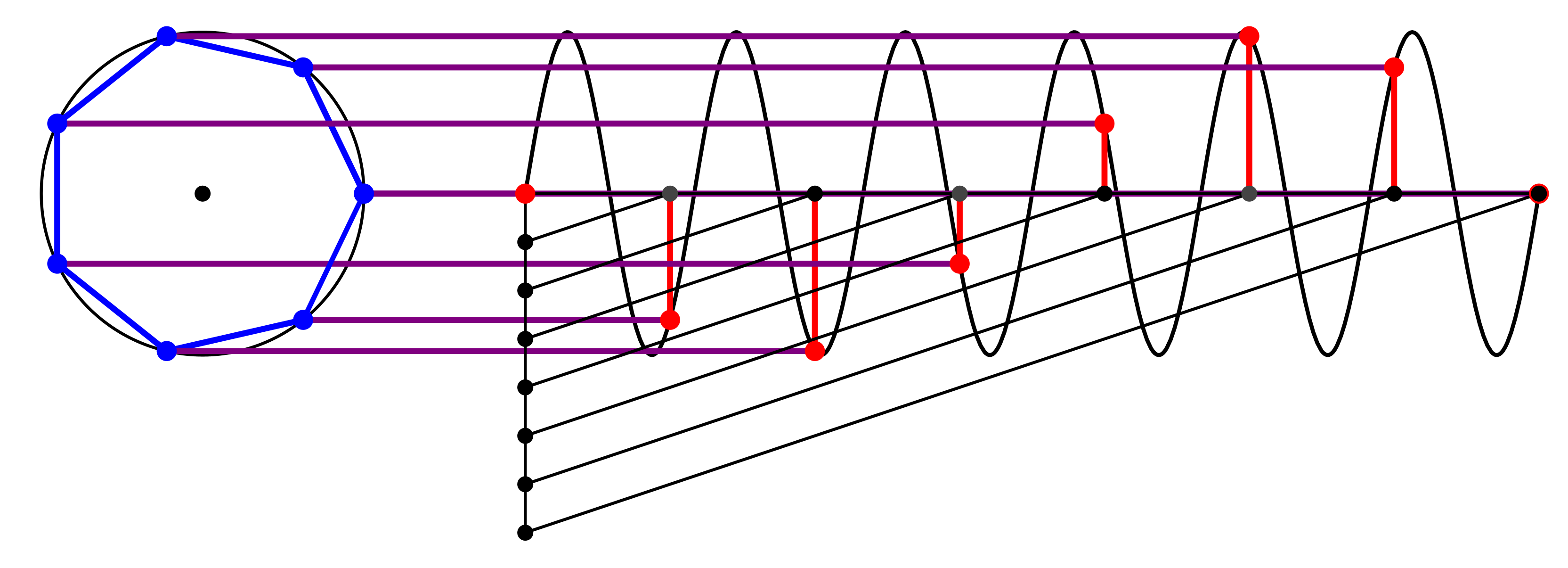
Ein Bild, das Reihe, Screenshot, Diagramm, Farbigkeit enthält.

Automatisch generierte Beschreibung

Abb. 12: Noch ein Siebeneck

Bei der Kreisfrequenz 7 wird es lustig (Abb. 13 und Abb. 14).

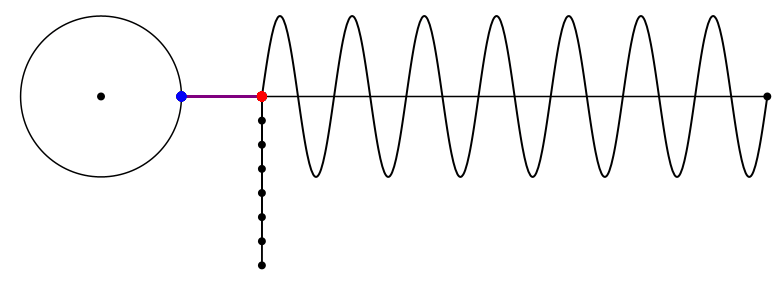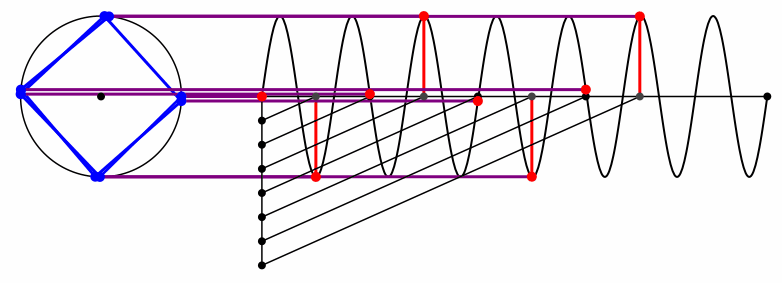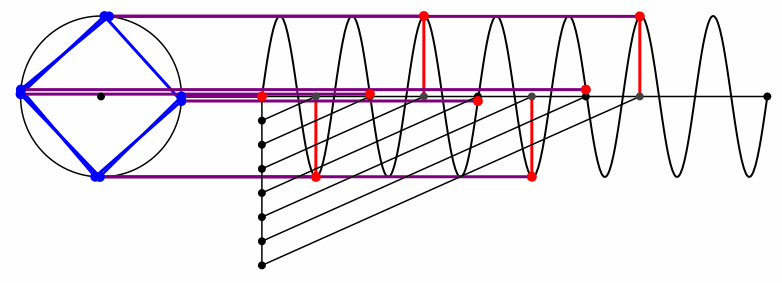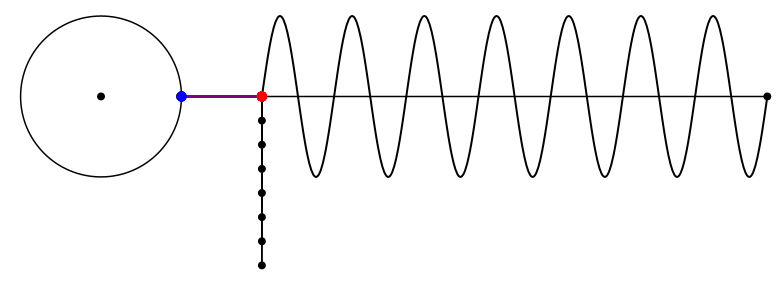
Abb. 13: Kreisfrequenz = 7

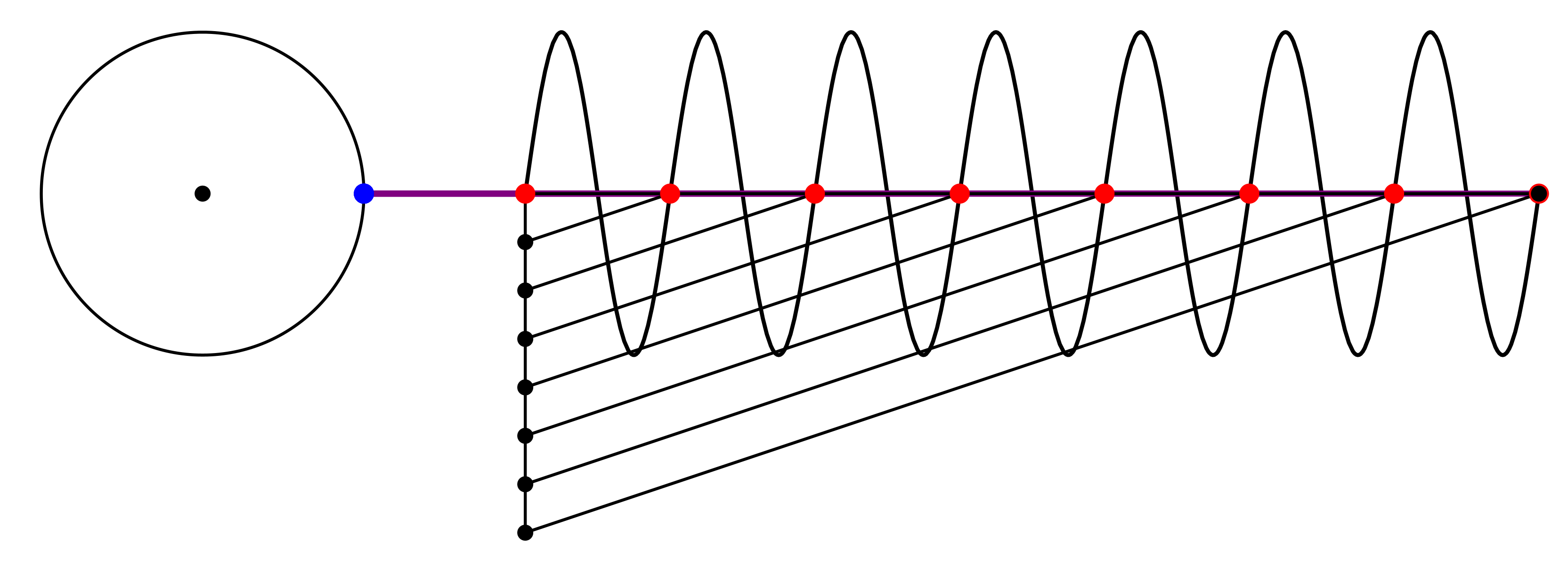
Ein Bild, das Screenshot, Dunkelheit enthält.

Automatisch generierte Beschreibung

Abb. 14: Viel Lärm um nichts

Bei der Kreisfrequenz 8 fängt es wieder von vorne an (Abb. 15).

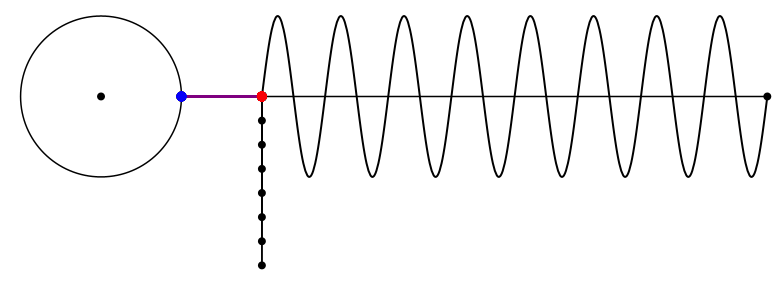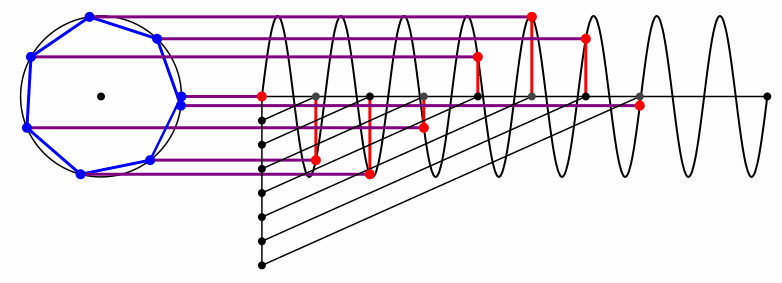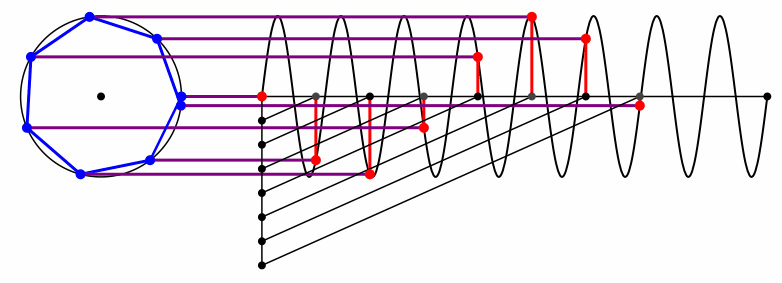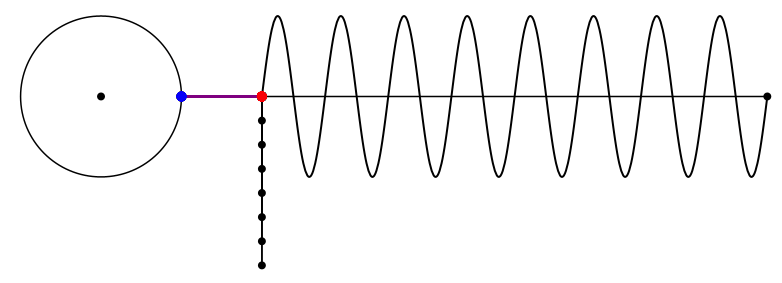
Abb. 15: Wieder das Siebeneck

In der Endlage (Abb. 16) sind die roten Punkte ebenfalls auf der gewöhnlichen Sinuskurve mit der Kreisfrequenz 1 (Abb. 2). Dies wegen 8 kongruent 1 modulo 7.

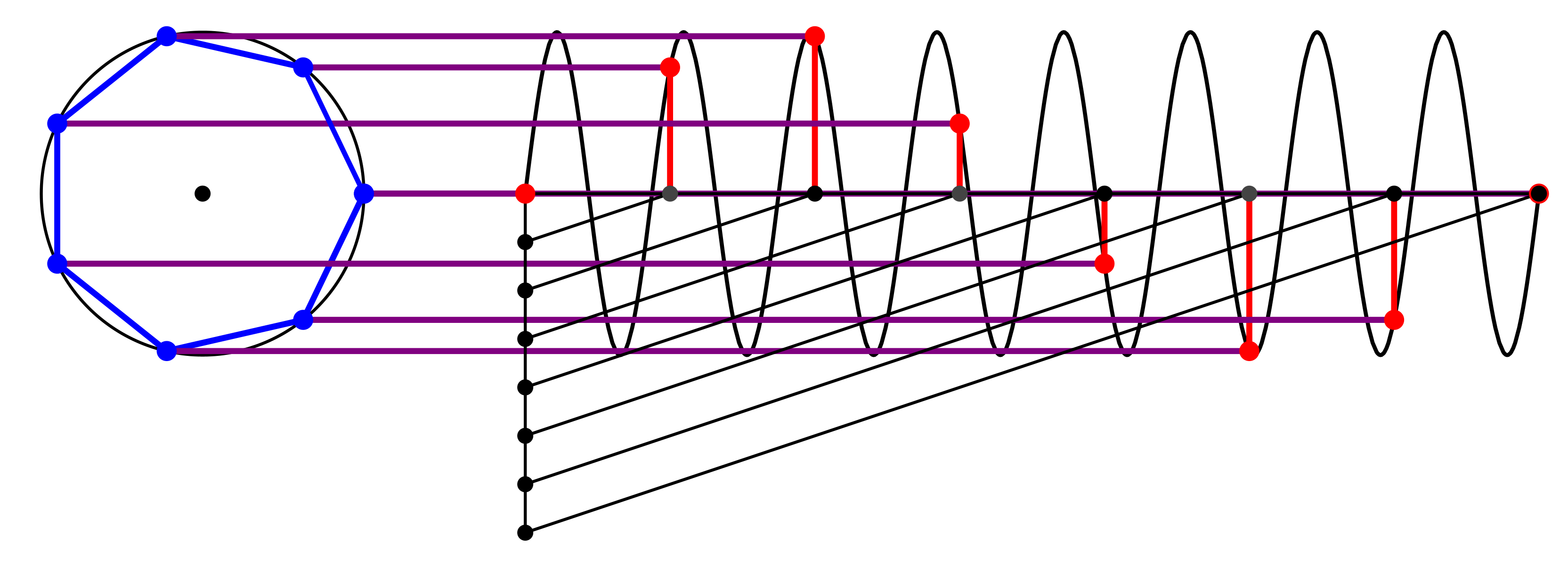
Ein Bild, das Reihe, Screenshot, Diagramm, Farbigkeit enthält.

Automatisch generierte Beschreibung